棣弗莫公式
设两个复数(用三角形式表示)Z1=r1(cosθ1+isinθ1),Z2=r2(cosθ2+isinθ2),则:
Z1Z2=r1r2[cos(θ1+θ2)+isin(θ1+θ2)]。
证:先讲一下复数的三角形式的概念。在复平面C上,用向量Z(a,b)来表示Z=a+bi。于是,该向量可以分成两个在实轴,
虚轴上的分向量.如果向量Z与实轴的夹角为θ,这两个分向量的模分别等于rcosθ,rsinθ(r=√a^2+b^2)。
所以,复数Z可以表示为Z=r(cosθ+isinθ)。这里θ称为复数Z的辐角。
因为Z1=r1(cosθ1+isinθ1),Z2=r2(cosθ2+isinθ2),所以
Z1Z2=r1r2(cosθ1+isinθ1)(cosθ2+isinθ2)
=r1r2(cosθ1cosθ2+icosθ1sinθ2+isinθ1cosθ2-sinθ1sinθ2)
=r1r2[(cosθ1cosθ2-sinθ1sinθ2)+i(cosθ1sinθ2+sinθ1cosθ2)]
=r1r2[cos(θ1+θ2)+isin(θ1+θ2)]
实际上由欧拉恒等式:e^ix = cosx + isinx,就可以得到上面的式子。
其实该定理可以推广为一般形式: 设n个复数Z1=r1(cosθ1+isinθ1),Z2=r2(cosθ2+isinθ2),……,Zn=rn(cosθn+isinθn),则: Z1Z2……Zn=r1r2……rn[cos(θ1+θ2+……+θn)+isin(θ1+θ2+……+θn)]. 实际上可以用棣弗莫公式来理解欧拉公式。 由棣弗莫公式可以得到: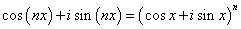
将其二项式展开即可得到n倍角公式。
其实该定理可以推广为一般形式: 设n个复数Z1=r1(cosθ1+isinθ1),Z2=r2(cosθ2+isinθ2),……,Zn=rn(cosθn+isinθn),则: Z1Z2……Zn=r1r2……rn[cos(θ1+θ2+……+θn)+isin(θ1+θ2+……+θn)]. 实际上可以用棣弗莫公式来理解欧拉公式。 由棣弗莫公式可以得到:
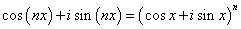
将其二项式展开即可得到n倍角公式。