脉冲神经元模型

传统的人工神经元模型主要包含两个功能，一是对前一层神经元传递的信号计算加权和，二是采用一个非线性激活函数输出信号。 前者用于模仿生物神经元之间传递信息的方式，后者用来提高神经网络的非线性计算能力。相比于人工神经元，脉冲神经元则从神经科学的角度出发，对真实的生物神经元进行建模。

Hodgkin-Huxley（ HH）模型

HH模型是一组描述神经元细胞膜的电生理现象的非线性微分方程，直接反映了细胞膜上离子通道的开闭情况。HH模型所对应的电路图如图1-1所示，其中 C 代表脂质双层(lipid bilayer) 的电容；RNa, RK, Rl分别代表钠离子通道、 钾离子通道与漏电通道的电阻（RNa, RK 上的斜箭头表明其为随时间变化的变量， 而 R l 则为一个常数）； E l, E Na, E K 分别代表由于膜内外电离子浓度差别所导致的漏电平衡电压、钠离子平衡电压、钾离子平衡电压；膜电压V代表神经膜内外的电压差，可以通过HH模型的仿真来得到V随时间变化的曲线。神经元的膜电压变化，如图1-2所示。图中共有6个输入脉冲（垂直虚线所示），每个脉冲触发膜电压V的快速上升。如果输入脉冲之间的时间间隔较长（例如在1ms与22ms到达的2个脉冲之间，由于漏电通道的作用，没有新的输入脉冲），膜电压V就会随着时间逐渐降低至平衡电压El。如果有多个输入脉冲在短时间内连续到达（例如在45~50ms 之间的3 个脉冲），那么膜电压V会上升至发放阈值Vth（红 {MOD}水平虚线所示） 而触发一个输出脉冲。之后V被重置为低于平衡电压El的Vreset，然后逐渐回升至平衡电压El。神经元的行为与输入的时间特性密切相关，一组脉冲如果在短时间内连续到达，可以触发神经元的脉冲；但是同样数量的一组脉冲如果在较长时间内分散到达，那么膜电压的漏电效应便不会产生脉冲。HH模型精确地描绘出膜电压的生物特性，能够很好地与生物神经元的电生理实验结果相吻合，但是运算量较高，难以实现大规模神经网络的实时仿真。

Leaky Integrate and Fire(LIF)模型

为了解决HH模型运算量的问题，许多学者提出了一系列的简化模型。LIF模型将细胞膜的电特性看成电阻和电容的组合。

Izhikevich模型

HH模型精确度高，但运算量大。LIF模型运算量小，但牺牲了精确度。Izhikevich模型结合了两者的优势，生物精确性接近HH模型，运算复杂度接近LIF模型。

神经脉冲序列

在完成神经元的建模之后，需要对神经元传递的信息进行编码，一种主流的方法是通过神经元的放电频率来传递信息。在大脑皮层，连续动作电位的时序非常没有规律。一种观点认为这种无规律的内部脉冲间隔反映了一种随机过程，因此瞬时放电频率可以通过求解大量神经元的响应均值来估计。另一种观点认为这种无规律的现象可能是由突触前神经元活动的精确巧合所形成的，反映了一种高带宽的信息传递通路。本文主要基于第一种观点，用随机过程的方法生成脉冲序列。

瞬时放电频率

神经元的响应函数有一系列的脉冲函数所构成，如公式所示。ρ(t)=∑ki=1δ(t−ti)其中，k表示某个脉冲序列中的脉冲数， 表示每个脉冲到达的时间。由脉冲函数的性质可得，在时间间隔 内，脉冲数可通过公式来计算。n=∫t2t1ρ(t)dt因此瞬时放电频率可定义为神经元响应函数的期望，如公式所示。r(t)=dn(t)dt=E(ρ(t))根据概率学统计理论，以某一小段时间间隔内的神经元响应函数的均值来作为放电频率的估计值，如公式所示。rM(t)=1M∑Mj=1ρj(t)

齐次泊松过程

假设每个脉冲的生成是相互独立的，并且瞬时放电频率是一个常数。设时间段 内含有k个脉冲，那么在时间段 内含有n个脉冲的概率可由公式表示。P(n,t1,t2)=k!(k−n)!n!pnqk−n其中，p=(t2−t1)T，q=1−p 。令k趋于无穷大，同时平均放电频率 保持不变，得到P(n,t1,t2)=e−rΔtrΔtnn!可以看出，上式与泊松分布的概率密度函数形式相同，进一步说明了脉冲发放过程可用泊松过程来模拟。

泊松脉冲序列的生成

相邻脉冲间的时间间隔固定

对于齐次泊松过程，在固定时间间隔δt内，产生一个脉冲的概率为P(n=1)≈rΔt因此，以泊松模型产生神经脉冲序列的方法如下。选取一个固定的时间间隔，产生一个 区间的符合均匀分布的随机数x[i]。对于每一个间隔，如果x[i]≤rΔt ，则发放一个脉冲，否则不产生脉冲。在实践中，时间间隔必须足够小，产生的脉冲才会近似符合泊松分布。

相邻脉冲见的时间间隔不固定

根据上面的讨论，在间隔[t0,t0+τ]内，发放的脉冲数为0的概率为P(n=0)=e−rτ因此，在时刻t0+τ之前发放脉冲的概率可表示为P(τ)=1−e−rτ那么，相邻两个脉冲之间的等待时间的概率密度分布可表示为p(τ)=d(1−e−rτ)dt=re−rτ由此，产生神经脉冲序列的方法如下。当一个脉冲发放完成之后，从符合指数分布的随机数集合中随机选择一个数作为下一次发放脉冲需等待的时间。依次类推，便可产生符合泊松模型的神经脉冲序列。

扩展

非齐次泊松过程

相较于齐次泊松过程，非齐次泊松模型假设放电频率是时间的函数 ，更具有一般性。只有间隔 足够小，那么在这段时间内，放电频率仍可以视为常数。上述的理论依然有效。

不应期

根据神经科学理论，神经元在放电之后的短暂时间内存在不应期，即对输入信号不响应。为了在脉冲序列中模拟这个过程，在神经元放电之后的不应期内将瞬时放电频率置为0。在不应期结束之后，瞬时放电频率 在限定时间内逐渐回到原始值。

涌现

神经元在某个时刻会集中性的放电，称为涌现现象。为了模拟这种现象，设置每个时刻发放的泊松脉冲数不固定，可能包含0，1，或多个脉冲。每个时刻发放的脉冲数符合一定的概率分布。例如，设x是 上符合均匀分布的一个随机数，当x取不同值时，该时刻发放的脉冲数也不同。

脉冲神经网络的训练方法

人工神经网络主要基于误差反向传播（BP）原理进行有监督的训练，目前取得很好的效果。对于脉冲神经网络而言，神经信息以脉冲序列的方式存储，神经元内部状态变量及误差函数不再满足连续可微的性质，因此传统的人工神经网络学习算法不能直接应用于脉冲神经神经网络。目前，脉冲神经网络的学习算法主要有以下几类。

无监督学习算法

这类算法从生物可解释性出发，主要基于赫布法则 (Hebbian Rule)。Hebb在关于神经元间形成突触的理论中提到，当两个在位置上临近的神经元，在放电时间上也临近的话，他们之间很有可能形成突触。而突触前膜和突触后膜的一对神经元的放电活动（spike train）会进一步影响二者间突触的强度。这个假说也得到了实验验证。华裔科学家蒲慕明和毕国强在大树海马区神经元上，通过改变突触前膜神经元和突触后膜神经元放电的时间差，来检验二者之间突触强度的变化。实验结果如图3-1所示。其中，EPSC表示突触强度。当EPSP(兴奋性脉冲)在spike之前产生，突触强度增强。当EPSP在spike之后产生，突触强度减弱。这个现象被称为脉冲序列相关的可塑性（Spike Timing Dependent Plasticity，STDP）。
基于该生物现象，提出了两种主流的无监督STDP学习算法。

三相STDP

权值更新规则如公式所示。其中， A+和A− 表示学习率， 表示突触前脉冲传到突触后脉冲所需的时间。函数关系如图3-2所示。

二相STDP

权值更新规则如公式所示。其中， τ+和τ− 用来控制电压下降的速度，被视为时间常数。函数关系如图3-3所示。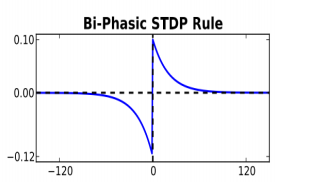

有监督学习算法

有监督学习算法依据是否具有生物可解释性分为两大类，一种是基于突触可塑性的监督学习算法，另外两种分别是基于梯度下降规则的监督学习算法和基于脉冲序列卷积的监督学习算法。

基于突触可塑性的监督学习算法

监督Hebbian学习算法

通过“教师”信号使突触后神经元在目标时间内发放脉冲，“教师”信号可以表示为脉冲发放时间，也可以转换为神经元的突触电流形式。在每个学习周期，学习过程由3个脉冲决定，包括2个突触前脉冲和1个突触后脉冲。第一个突触前脉冲表示输入信号，第二个突触前脉冲表示突触后神经元的目标脉冲，权值的学习规则可表示为Δw=η(tfo−tfd)其中，η表示学习率，tfo 和tfd 分别表示突触后神经元的实际和目标脉冲时间。

远程监督学习算法（ReSuMe）

远程监督方法结合STDP和anti-STDP两个过程，提出的突触权值随时间变化的学习规则为其中，Si和So 分别表示突触前输入脉冲序列和突触后输出脉冲序列， Sd表示目标脉冲序列，对于兴奋性突触，ad参数 取正值，学习窗口 adi(s)表示为STDP规则；对于抑制性突触，ad参数 取负值， adi(s)表示为anti-STDP规则。应用ReSuMe算法训练脉冲神经网路，突触权值的调整仅依赖于输入输出的脉冲序列和STDP机制，与神经元模型无关，因此该算法可适用于各种神经元模型。后来针对该算法的改进，使得ReSuMe算法可应用到多层前馈脉冲神经网络。

其他监督学习算法

结合BCM（Bienenstock-Cooper-Munro）学习规则和STDP机制，Wade等人提出了多层前馈脉冲神经网络的SWAT(Synaptic Weight Association Training)算法。研究者应用奖惩调制的STDP机制实现了脉冲神经网络脉冲序列模式的学习。此外，有学者从统计学的角度出发提出了一种脉冲神经网络的监督学习算法，学习规则可有一个类似于STDP的二阶学习窗口来描述，学习窗口的形状是通过优化过程的不同场景所加入的约束来影响的。基于脉冲序列卷积的监督学习算法,通过对脉冲序列基于核函数的卷积计算，可将脉冲序列解释为特定的神经生理信号，比如神经元的突触后电位或脉冲发放的密度函数。通过脉冲序列的内积来定量地表示脉冲序列之间的相关性，评价实际脉冲序列与目标脉冲序列的误差。基于梯度下降的监督学习算法。借鉴传统人工神经网络的误差反向传播算法，利用神经元目标输出与实际输出之间的误差，应用梯度下降法和delta更新规则更新权值。比如SpikiProp算法

ANN向SNN的转化

由于脉冲神经网络的训练算法不太成熟，一些研究者提出将传统的人工神经网络转化为脉冲神经网络，利用较为成熟的人工神经网络训练算法来训练基于人工神经网络的深度神经网络，然后通过触发频率编码将其转化为脉冲神经网络，从而避免了直接训练脉冲神经网络的困难。

CNN转化为SNN

对原始的CNN进行训练，将训练好的权值直接迁移到相似网络结构的SNN。

困难

CNN中的某一层神经元可能会输出负值，这些负数用SNN表示会比较困难。比如，CNN中的sigmoid函数的输出范围为-1到1，每个卷积层的加权和可能也为负值，在进行颜 {MOD}空间变换时某个颜 {MOD}通道也可能取到负值。虽然，SNN可以采用抑制神经元来表示负值，但会成倍地增加所需要的神经元数目，提高计算的复杂度。对于SNN，CNN中神经元的偏置很难表示。CNN中的Max-pooling层对应到SNN中，需要两层的脉冲神经网络。同样提高了SNN的复杂度。

裁剪

a. 保证CNN中的每个神经元的输出值都是正数。在图像预处理层之后，卷积层之前加入abs()绝对值函数，保证卷积层的输入值都是非负的。将神经元的激活函数替换为ReLU函数。一方面可以加快原始CNN的收敛速度，另一方面ReLU函数和LIF神经元的性质比较接近，可以最小化网络转化之后的精度损失。
b. 将CNN所有的偏置项都置为0。
c. 采用空间线性降采样层代替Max-pooling层。

转化

a. SNN的网络结构与裁剪后的CNN相同，单纯地将CNN中的人工神经元替换为脉冲神经元
b. 在CNN的卷积层之前增加用于脉冲序列生成的一层网络，对输入的图像数据进行编码，转化为脉冲序列。
c. 变换决策方式。在某一段时间内，对全连接层输出的脉冲数进行统计，取脉冲数最多的类别作为最终的分类结果
d. 将裁减后的CNN训练得到的权值全部迁移到对应的SNN。
最终的转化结果如图4-1所示。

改进

将ANN转化为SNN造成准确度下降的主要原因是转化后的SNN容易产生过激活（over-activate）和欠激活（under-activate）现象。
a. 神经元的输入脉冲不够，导致神经元的膜电压无法超过设定的阈值，造成放电频率过低。
b. 神经元的输入脉冲过多，导致ReLU模型在每个采样周期内输出多个脉冲。
c. 因为脉冲序列输入是以一定的概率选择的，会导致某些特征一直处于边缘地带或占据了过多的主导地位。
因此，需要对训练得到的权值进行归一化操作。一种是基于模型的归一化操作。考虑所有可能的输入值，选择最大的可能输入值作为归一化因子，这样就保证了最大的可能输入只能产生一个脉冲。另一种是基于数据的归一化操作。输入训练集，找出最大的输入值作为归一化因子。这两种方法原理相同，前者考虑的是最坏情况，后者考虑的是一般情况。

参考文献

[1] Gerstner W, Kistler W M. Spiking neuron models: Single neurons, populations, plasticity[M]. Cambridge university press, 2002.
[2] Izhikevich E M. Simple model of spiking neurons[J]. IEEE Transactions on neural networks, 2003, 14(6): 1569-1572.
[3] Izhikevich E M. Hybrid spiking models[J]. Philosophical Transactions of the Royal Society of London A: Mathematical, Physical and Engineering Sciences, 2010, 368(1930): 5061-5070.
[4] Heeger D. Poisson model of spike generation[J]. Handout, University of Standford, 2000, 5: 1-13.
[5] Hebb D O. The organization of behavior: A neuropsychological theory[M]. Psychology Press, 2005.
[6] Caporale N, Dan Y. Spike timing-dependent plasticity: a Hebbian learning rule[J]. Annu. Rev. Neurosci., 2008, 31: 25-46.
[7] Ponulak F, Kasinski A. Supervised learning in spiking neural networks with ReSuMe: sequence learning, classification, and spike shifting[J]. Neural Computation, 2010, 22(2): 467-510.
[8] Wade J J, McDaid L J, Santos J A, et al. SWAT: a spiking neural network training algorithm for classification problems[J]. IEEE Transactions on neural networks, 2010, 21(11): 1817-1830.
[9] Rumelhart D E, Hinton G E, Williams R J. Learning representations by back-propagating errors[J]. Cognitive modeling, 1988, 5(3): 1.
[10] Bohte S M, Kok J N, La Poutre H. Error-backpropagation in temporally encoded networks of spiking neurons[J]. Neurocomputing, 2002, 48(1): 17-37.
[11] Ghosh-Dastidar S, Adeli H. A new supervised learning algorithm for multiple spiking neural networks with application in epilepsy and seizure detection[J]. Neural networks, 2009, 22(10): 1419-1431.
[12] Mohemmed A, Schliebs S, Matsuda S, et al. Span: Spike pattern association neuron for learning spatio-temporal spike patterns[J]. International Journal of Neural Systems, 2012, 22(04): 1250012.
[13] Mohemmed A, Schliebs S, Matsuda S, et al. Training spiking neural networks to associate spatio-temporal input–output spike patterns[J]. Neurocomputing, 2013, 107: 3-10.
[14] Yu Q, Tang H, Tan K C, et al. Precise-spike-driven synaptic plasticity: Learning hetero-association of spatiotemporal spike patterns[J]. Plos one, 2013, 8(11): e78318.
[15] Cao Y, Chen Y, Khosla D. Spiking deep convolutional neural networks for energy-efficient object recognition[J]. International Journal of Computer Vision, 2015, 113(1): 54-66.
[16] Diehl P U, Neil D, Binas J, et al. Fast-classifying, high-accuracy spiking deep networks through weight and threshold balancing[C]//2015 International Joint Conference on Neural Networks (IJCNN). IEEE, 2015: 1-8.
[17] O’Connor P, Neil D, Liu S C, et al. Real-time classification and sensor fusion with a spiking deep belief network[J]. Neuromorphic Engineering Systems and Applications, 2015: 61.
[18] Maass W, Natschläger T, Markram H. Real-time computing without stable states: A new framework for neural computation based on perturbations[J]. Neural computation, 2002, 14(11): 2531-2560.
[19] LIN X, WANG X, ZHANG N, et al. Supervised Learning Algorithms for Spiking Neural Networks: A Review[J]. Acta Electronica Sinica, 2015, 3: 024.
[20] 顾宗华, 潘纲. 神经拟态的类脑计算研究[J]. 中国计算机学会通讯, 2015, 11(10): 10-20.