随机模拟方法简介

随机模拟方法又称为蒙特卡罗方法（Monte Carlo Method）。蒙特卡洛模拟方法的原理是当问题或对象本身具有概率特征时，可以用计算机模拟的方法产生抽样结果，根据抽样计算统计量或者参数的值；随着模拟次数的增多，可以通过对各次统计量或参数的估计值求平均的方法得到稳定结论。由于涉及到时间序列的反复生成，蒙特卡洛模拟法是以高容量和高速度的计算机为前提条件的，因此只是在近些年才得到广泛推广。
从上面的描述我们不难看出随机模拟方法主要是针对那些确定算法不好解或者解不出来的情况。因此是一种典型的寻求近似解的方法。

基本思路

1. 针对实际问题建立一个简单易行的概率统计模型，使问题所求的解为该模型的概率分布或者数字特征，比如：某个事件的概率或者是某个随机变量的期望值。
2. 对模型中的随机变量建立抽样方法，在计算机上进行模拟试验，得到足够的随机抽样，并对相关事件进行统计
3. 对试验结果进行分析，给出所求解的估计及其精度（方差）的估计

蒙特卡罗方法在数学中的应用

参考维基百科 通常蒙特卡洛方法通过构造匹配一定规则的随机数来解决数学上的各种问题。对于那些由于计算过于复杂而难以得到解析解或者根本没有解析解的问题，蒙特卡洛方法是一种有效的求出数值解的方法。一般蒙特卡洛方法在数学中最常见的应用就是蒙特卡洛积分。下面是蒙特卡罗方法的两个简单应用：

圆周率

蒙特卡洛方法可用于近似计算圆周率：让计算机每次随机生成两个0到1之间的数，看以这两个实数为横纵坐标的点是否在单位圆内。生成一系列随机点，统计单位圆内的点数与总点数，（圆面积和正方形面积之比为PI:4，PI为圆周率），当随机点获取越多时，其结果越接近于圆周率（然而准确度仍有争议：即使取10的9次方个随机点时，其结果也仅在前4位与圆周率吻合）。用蒙特卡洛方法近似计算圆周率的先天不足是：第一，计算机产生的随机数是受到存储格式的限制的，是离散的，并不能产生连续的任意实数；上述做法将平面分区成一个个网格，在空间也不是连续的，由此计算出来的面积当然与圆或多或少有差距。

蒙特卡罗积分

举个简单的例子，假设我们要求f(x)的积分∫baf(x)dx
但是f(x)的形式比较复杂不好求积分，使用蒙特卡罗积分方法转化为∫baf(x)q(x)q(x)dx
把q(x)看作是x在区间[a,b]内的概率分布，前面的分数部分看做一个函数，然后再q(x)下抽取n个样本，当n足够大时，可以利用均值来近似（大数定理），1n∑if(xi)p(xi)
因此只要q(x)比较容易采样就行。 随机模拟三个要素：随机数，逻辑模型，反复试验。其基本思路就是要把待解决的问题转化为一种可以通过某种采样方法可以解决的问题，因此随机模拟方法的核心就是如何对一个概率分布得到样本，即抽样（sampling）。

常见的采样方法

直接采样

通过对均匀分布采样，实现对任意分布采样。 一般而言均匀分布 Uniform(0,1)的样本是相对容易生成的。 通过线性同余发生器可以生成伪随机数，我们用确定性算法生成[0,1]之间的伪随机数序列后，这些序列的各种统计指标和均匀分布 Uniform(0,1) 的理论计算结果非常接近。这样的伪随机序列就有比较好的统计性质，可以被当成真实的随机数使用。 而我们常见的概率分布，无论是连续的还是离散的帆布，都可以基于Uniform(0,1)的样本生成。 直接采样步骤：

1. 从Uniform(0,1)随机产生一个样本z
2. 另z=h(y)，其中h(y)为y的累积概率分布CDF
3. 计算y=h−1(z)
4. 结果y为对p(y)的采样

注：需要知道累积概率分布的解析表达式，且累积概率分布函数存在反函数
但是如果h(x)不能确定或者没有无法解析求逆则直接抽样不再合适。对于复杂的现实模型其实是不常用的。

接受-拒接采样

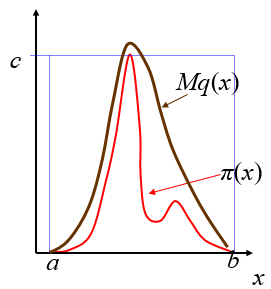
简称拒绝采样，基本思想：假设我们需要对一个分布f(x)进行采样，但是却很难直接进行采样，所以我们想通过另外一个容易采样的分布g(x)的样本，用某种机制去除掉一些样本，从而使得剩下的样本就是来自与所求分布f(x)的样本。

1. 给定目标分布密度π(x)
2. 建议密度（proposal density）q(x)和常数M，使得
   对q(x)采样比较容易
   q(x)的形状比较接近π(x)
   对任意x，有π(x)≤Mq(x)（包络原则）
3. 通过对q(x)采样实现对π(x)采样
   
   采样过程：
   产生样本X∼q(x)，和U∼Uniform[0,1]
   若U≤π(X)/Mq(x)，则接受X，接受的样本服从分布π(x)
   等价于：
   Y=Mq(X)U，若Y≤π(X)，则接受X

在高维空间，接受-拒绝采样会出现两个问题，一是合适的proposal density q(x)比较难找，而是很难确定一个准确的M值。这两个问题会导致拒绝率很高，无用计算增加。

重要性采样

通过从已知采样的概率q(x)采样，近似积分
I=∫f(x)π(x)dx=∫f(x)π(x)q(x)q(x)dx
从q(x)中抽取N个样本，上述式子就约等于1N∑Nif(xi)π(xi)q(xi)。这相当于给每一个样本赋予了一个权重w(xi)=π(xi)q(xi)，q(x)大意味着概率大，那么N里面含有这个样本的xi就多，即这些样本的权重大，所以称之为重要性抽样。下面这个链接里关于重要性采样的理解写的很形象：
http://blog.sina.com.cn/s/blog_4e5740460100cw5b.html
采样过程：

1. 选择一个容易抽样的分布q(x)，产生N个样本X1,...,XN∼q(x)
2. 近似解：