中国剩余定理(CRT)的表述如下
设正整数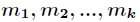 两两互素,则同余方程组
两两互素,则同余方程组
 有整数解。并且在模
有整数解。并且在模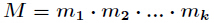 下的解是唯一的,解为
下的解是唯一的,解为
 其中
其中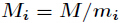 ,而
,而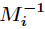 为
为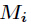 模
模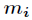 的逆元。
的逆元。
普通的中国剩余定理要求所有的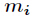 互素,那么如果不互素呢,怎么求解同余方程组?
这种情况就采用两两合并的思想,假设要合并如下两个方程
互素,那么如果不互素呢,怎么求解同余方程组?
这种情况就采用两两合并的思想,假设要合并如下两个方程
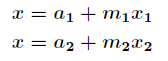 那么得到
那么得到
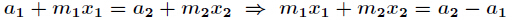 在利用扩展欧几里得算法解出
在利用扩展欧几里得算法解出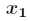 的最小正整数解,再带入
的最小正整数解,再带入
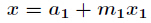 得到
得到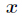 后合并为一个方程的结果为
后合并为一个方程的结果为
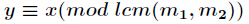 这样一直合并下去,最终可以求得同余方程组的解。
这样一直合并下去,最终可以求得同余方程组的解。
原来文章地址:http://blog.csdn.net/acdreamers/article/details/8050018
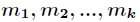 两两互素,则同余方程组
两两互素,则同余方程组
 有整数解。并且在模
有整数解。并且在模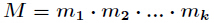 下的解是唯一的,解为
下的解是唯一的,解为
 其中
其中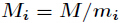 ,而
,而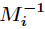 为
为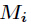 模
模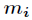 的逆元。
的逆元。
int CRT(int a[],int m[],int n)
{
int M = 1;
int ans = 0;
for(int i=1; i<=n; i++)
M *= m[i];
for(int i=1; i<=n; i++)
{
int x, y;
int Mi = M / m[i];
extend_Euclid(Mi, m[i], x, y);
ans = (ans + Mi * x * a[i]) % M;
}
if(ans < 0) ans += M;
return ans;
} 普通的中国剩余定理要求所有的
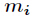 互素,那么如果不互素呢,怎么求解同余方程组?
这种情况就采用两两合并的思想,假设要合并如下两个方程
互素,那么如果不互素呢,怎么求解同余方程组?
这种情况就采用两两合并的思想,假设要合并如下两个方程
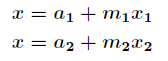 那么得到
那么得到
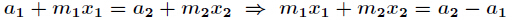 在利用扩展欧几里得算法解出
在利用扩展欧几里得算法解出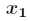 的最小正整数解,再带入
的最小正整数解,再带入
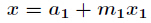 得到
得到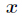 后合并为一个方程的结果为
后合并为一个方程的结果为
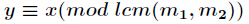 这样一直合并下去,最终可以求得同余方程组的解。
这样一直合并下去,最终可以求得同余方程组的解。
原来文章地址:http://blog.csdn.net/acdreamers/article/details/8050018