1 定义 向量，指具有大小和方向的量。
2 向量的记法：印刷体记作粗体的字母（下文所有未说明的字母都为向量），书写时在字母顶上加一小箭头“→”

3 向量的长度叫做向量的模。符号是|...|     (形同绝对值符号) 模为0的向量是零向量（方向不确定），模为1的向量是单位向量
4 向量的加减法：（如图） 加法： 1 首位相接，结果是从第一个始点到最后一个终点的向量； 2 平行四边形法则，同始点的两个向量相加得到得向量是以它们两边的平行四边形的对角线，始点与它们相同. 减法： 1 可以利用相反向量，a-b = a+（-b） 2 减法是加法的逆运算. 如果a+b=c，那么a = c - b 向量是可以这个用道理进行减法 AB - AC = CB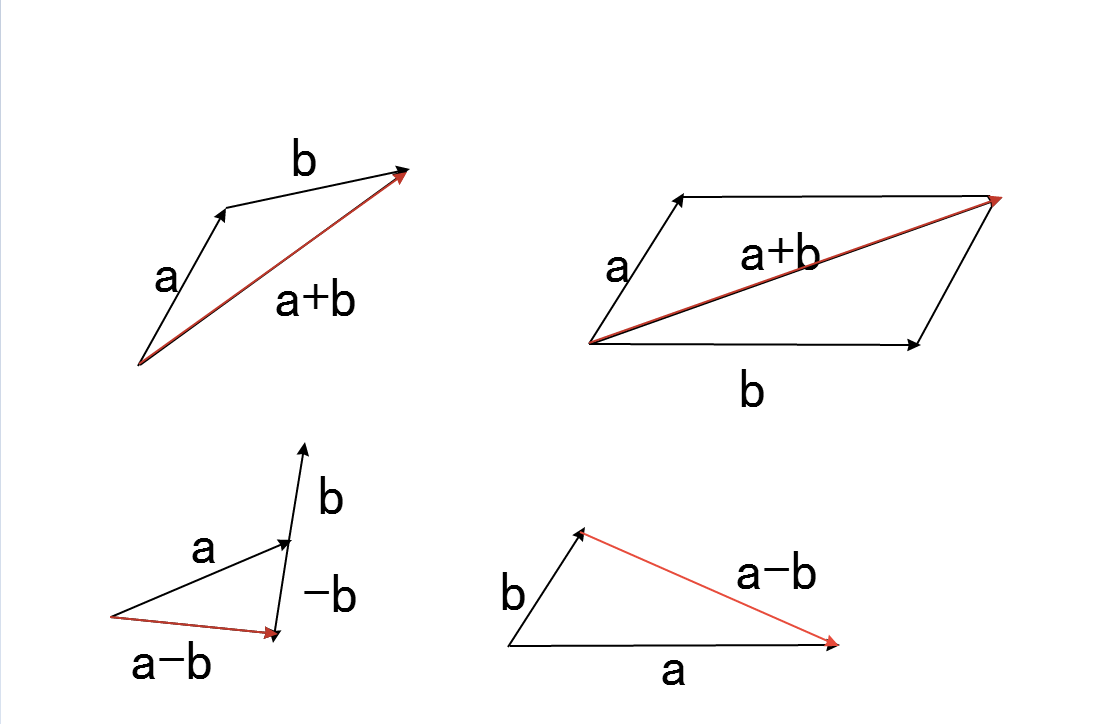  

5 向量的坐标表示 将向量放入平面直角坐标系中，使其始点是原点，终点的坐标就是向量的坐标
6 向量的数乘：功能是放缩. 坐标运算：a(x, y).  λa=(λx,λy)； 应用：判断向量共线 a(x1, y1), b(x2, y2) a // b⇔x1*y2-y1*x2 = 0
7 向量的数量积(点乘、内积)：是a的模乘以b的模乘以它们夹角的余弦值 a · b = |a| |b| cos 坐标运算：a(x1, y1), b(x2, y2).  a · b = x1 * x2 + y1 * y2 应用：判断向量垂直 a ⊥ b⇔a · b = 0
8 向量的向量积(叉乘、外积)：以a，b为两边组成的三角形有向面积的2倍. 坐标运算：a(x1, y1), b(x2, y2).  a × b = x1 * y2 + y1 * x2 应用： 1 判断向量共线 a // b⇔a × b = 0（本质是数乘）



------------------------- 例1 ： 判断点与三角形的位置关系

题目描述

判断一个点与已知三角形的位置关系。

输入输出格式

输入格式：
前三行：每行一个坐标，表示该三角形的三个顶点 第四行：一个点的坐标，试判断该点与前三个点围成三角形的位置关系 所有坐标值均为整数。 输出格式：
若点在三角形内（不含边界），输出1； 若点在三角形外（不含边界），输出2； 若点在三角形边界上（不含顶点），输出3； 若点在三角形顶点上，输出4。

输入输出样例

输入样例#1：  (0,0) (3,0) (0,3) (1,1) 输出样例#1：  1

【code】
#include #include #include using namespace std; struct Vector { int x, y; Vector(int x=0, int y=0):x(x), y(y) {} }; typedef Vector Point; Vector operator -(const Point a, const Point b) { return Vector(a.x-b.x, a.y-b.y); } bool operator ==(const Point a, const Point b) { return (a.x == b.x && a.y == b.y); } double cross(const Vector a, const Vector b) { return a.x * b.y - b.x * a.y; } bool On_Edge(Point a, Point b, Point x) { if(min(a.x, b.x) <= x.x && x.x <= max(a.x, b.x) && min(a.y, b.y) <= x.y && x.y <= max(a.y, b.y)) if(cross(a-x, b-x) == 0) return true; return false; } bool In(Point x, Point a, Point b) { Vector A = x - a, B = b - a; if(cross(B, A) > 0) return true; return false; } int main() { Point a, b, c, x; scanf("(%d,%d) ", &a.x, &a.y); scanf("(%d,%d) ", &b.x, &b.y); scanf("(%d,%d) ", &c.x, &c.y); scanf("(%d,%d) ", &x.x, &x.y); if(x == a || x == b || x == c) printf("4"); else if(On_Edge(a, b, x) || On_Edge(a, c, x) || On_Edge(b, c, x)) printf("3"); else { if(cross(b-a, c-a) < 0) swap(b, c); if(In(x, a, b) && In(x, b, c) && In(x, c, a)) printf("1"); else printf("2"); } }