回忆版1、已知π/4≈1-1/3+1/5-......,表达式为(-1)^(i-1)/(2i-1),求π的近似值,误差小于10^-5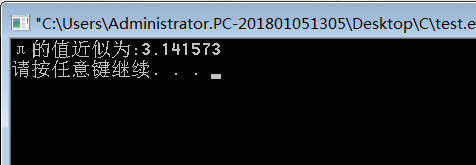 当把while循环条件改成>1e-7,即误差小于10^7,结果肥肠接近π值:
当把while循环条件改成>1e-7,即误差小于10^7,结果肥肠接近π值: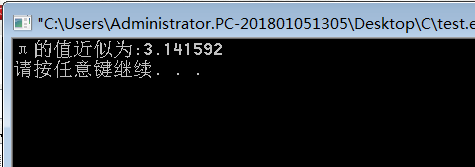
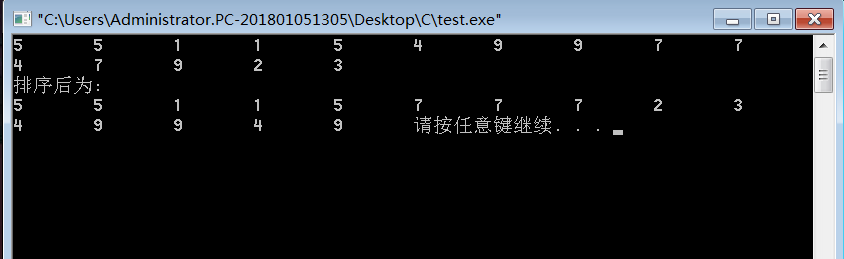
2、一个序列,有素数和非素数,要求排序,使所有素数位于非素数之前,相对位置不变。注意:函数返回数组,要用到指针
3、编写完整的函数,输入正整数N和D,如果N/D为无限循环小数,输出时小数点后面的第一个循环节用括号括起来,不显示后面的循环;不为循环小数则正常显示。(25分)
例如:3/4=0.75;5/6=0.8(3);10/3=3.(3)答案:http://mp.blog.csdn.net/postedit/79463648
4、有N个正方形,边长对应斐波那契值,将这些正方形拼成一个长方形,求长和宽以及每个正方形左下角点坐标思路:题目是这个意思:
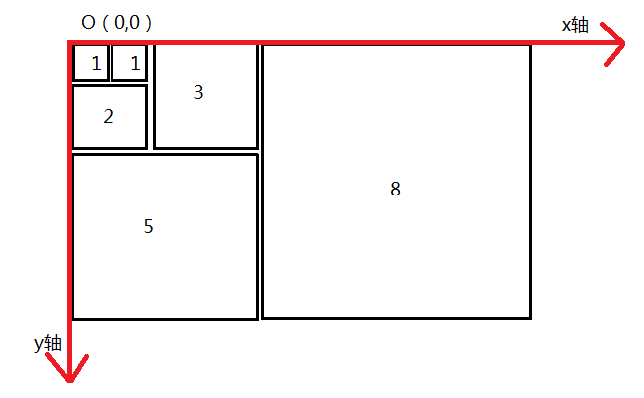
左下角点坐标分别为:(坐标系建立不唯一,故点坐标不唯一,但长方形的长宽是唯一的)(a为边长长度,也是斐波那契数列:1,1,2,3,5,8,13,21,34....)第1个正方形:a=1(0,1)长方形的长:1宽:1第2个正方形:a=1(1,1)长方形的长:2宽:1第3个正方形:a=2(0,3)长方形的长:3宽:2第4个正方形:a=3(2,3)长方形的长:5宽:3第5个正方形:a=5(0,8)长方形的长:8宽:5第6个正方形:a=8(5,8)长方形的长:13宽:8第7个正方形:a=13(0,21)长方形的长:21宽:13第8个正方形:a=21(13,21)长方形的长:34宽:21规律应该很容易看出来了,长宽:各自构成了斐波那契数列,长是从第二位开始点坐标:第i个正方形,若i是奇数,则x=0,y=长;若i是偶数,则x=上一个正方形构成的宽,y=上一个的长由此,可以建立四位数组:Fibonacci[N][4],第一位存宽,其余均可有宽推出
#include
#include
#define N 100
int main(){
double PIvalue();
double PI = PIvalue();
printf("π的值近似为:%f
",PI);
return 0;
}
double PIvalue(){
double Pi = 0;
int i=1;
double item=1;
while(fabs(item)>1e-5){//误差小于10^-5
if(i%2!=0)
Pi += item;
else
Pi -= item;
i++;
item = 1 / (double)(2 * i - 1);
}
return Pi*4;
}  当把while循环条件改成>1e-7,即误差小于10^7,结果肥肠接近π值:
当把while循环条件改成>1e-7,即误差小于10^7,结果肥肠接近π值:
2、一个序列,有素数和非素数,要求排序,使所有素数位于非素数之前,相对位置不变。注意:函数返回数组,要用到指针
#include
#include
#include
#define N 15
int main(){
int* sort(int A[]);
bool isPrime(int x);
int A[N],i;
srand(time(NULL));//种子,若不添加,再次运行的随机数不变
for(i=0;i=is_prime;j--)
B[j] = B[j-1];
B[is_prime] = A[i];
not_prime++;
is_prime++;
}else{
B[not_prime] = A[i];
not_prime++;
}
}
return B;
}
/*判断x是否为素数,是返回true,不是返回false*/
bool isPrime(int x){
int i;
bool is_prime=true;
for(i=2;i<=sqrt(x);i++)
if(x%i == 0){
is_prime = false;
break;
}
return is_prime;
} 
3、编写完整的函数,输入正整数N和D,如果N/D为无限循环小数,输出时小数点后面的第一个循环节用括号括起来,不显示后面的循环;不为循环小数则正常显示。(25分)
例如:3/4=0.75;5/6=0.8(3);10/3=3.(3)答案:http://mp.blog.csdn.net/postedit/79463648
4、有N个正方形,边长对应斐波那契值,将这些正方形拼成一个长方形,求长和宽以及每个正方形左下角点坐标思路:题目是这个意思:

左下角点坐标分别为:(坐标系建立不唯一,故点坐标不唯一,但长方形的长宽是唯一的)(a为边长长度,也是斐波那契数列:1,1,2,3,5,8,13,21,34....)第1个正方形:a=1(0,1)长方形的长:1宽:1第2个正方形:a=1(1,1)长方形的长:2宽:1第3个正方形:a=2(0,3)长方形的长:3宽:2第4个正方形:a=3(2,3)长方形的长:5宽:3第5个正方形:a=5(0,8)长方形的长:8宽:5第6个正方形:a=8(5,8)长方形的长:13宽:8第7个正方形:a=13(0,21)长方形的长:21宽:13第8个正方形:a=21(13,21)长方形的长:34宽:21规律应该很容易看出来了,长宽:各自构成了斐波那契数列,长是从第二位开始点坐标:第i个正方形,若i是奇数,则x=0,y=长;若i是偶数,则x=上一个正方形构成的宽,y=上一个的长由此,可以建立四位数组:Fibonacci[N][4],第一位存宽,其余均可有宽推出
#include
int main(){
void fibonacci(int n);
int n;
printf("请输入正方形个数:");
scanf("%d",&n);
fibonacci(n);
return 0;
}
void fibonacci(int n){
int Fibonacci[n][4];//第一位宽,第二位长,第三位x,第四位y
int i;
/**初始化**/
Fibonacci[0][0] = 1;
Fibonacci[1][0] = 1;
Fibonacci[0][1] = 1;
Fibonacci[1][1] = 2;
Fibonacci[0][2] = 0;
Fibonacci[1][2] = 1;
Fibonacci[0][3] = 1;
Fibonacci[1][3] = 1;
/**依次按规律赋值**/
for(i=2;i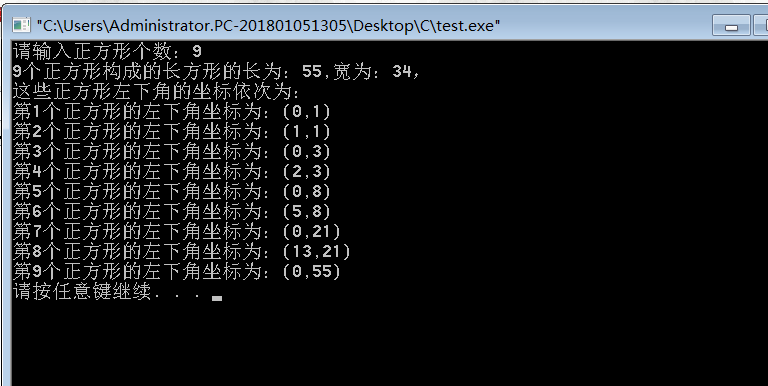
5、用四种颜 {MOD}给地图着 {MOD},要求相邻块颜 {MOD}不同,图用矩阵存储,求所有着 {MOD}方案。在另一篇中已写过了:http://blog.csdn.net/qq_21149391/article/details/79507153