本文是《视觉SLAM十四讲》第4讲的个人读书笔记,为防止后期记忆遗忘写的。
 的最小值.那么,就一定需要涉及到求导
的最小值.那么,就一定需要涉及到求导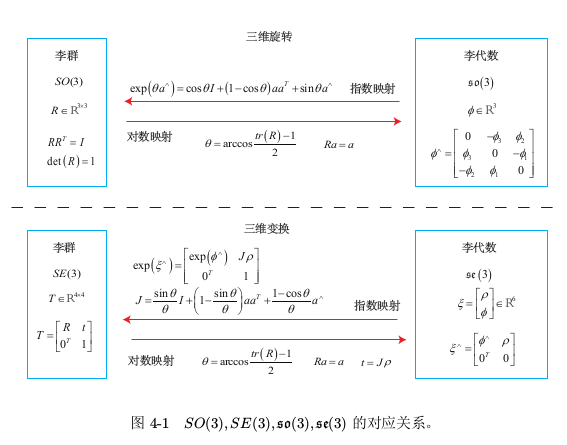 来求最小值的问题.而BCH 公式以及近似是推理基础,最终通过对不引入额外的约束的李群——李代数进行求导或者扰动模型近似来完成优化问题所需要的求导部分.
来求最小值的问题.而BCH 公式以及近似是推理基础,最终通过对不引入额外的约束的李群——李代数进行求导或者扰动模型近似来完成优化问题所需要的求导部分.
 我们发现它们对加法是不封闭的。换句话说,对于任意两个旋转矩阵 R 1 , R 2 ,它们按照矩阵加法的定义,和不再是一个旋转矩阵。这两种矩阵并没有良好定义的加法,但是相对的,它们只有一种较好的运算:乘法。SO(3) 和 SE(3) 关于乘法是封闭的:
我们发现它们对加法是不封闭的。换句话说,对于任意两个旋转矩阵 R 1 , R 2 ,它们按照矩阵加法的定义,和不再是一个旋转矩阵。这两种矩阵并没有良好定义的加法,但是相对的,它们只有一种较好的运算:乘法。SO(3) 和 SE(3) 关于乘法是封闭的:

 群(Group)是一种集合加上一种运算的代数结构。在群里,元素运算具有封闭性、结合律、幺元、逆的特点(参考离散数学)。变换矩阵和矩阵乘法也构成群(因此才能称它们为旋转矩阵群和变换矩阵群)。其他常见的群包括整数的加法 (Z, +),去掉 0 后的有理数的乘法(幺元为 1)(Q
群(Group)是一种集合加上一种运算的代数结构。在群里,元素运算具有封闭性、结合律、幺元、逆的特点(参考离散数学)。变换矩阵和矩阵乘法也构成群(因此才能称它们为旋转矩阵群和变换矩阵群)。其他常见的群包括整数的加法 (Z, +),去掉 0 后的有理数的乘法(幺元为 1)(Q
本节目标
- 总结李群与李代数的概念,知道为什么要引出它们。掌握 SO(3), SE(3) 与对应李代数的表示方式。
- 回忆 BCH 公式以及近似的意义。总结在李代数上的扰动模型。
- 使用 Sophus 对李代数进行运算。
这一节的知识点串联思路
在 SLAM 中,除了表示位姿之外,我们还要对它们进行估计和优化。因为在 SLAM 中位姿是未知的,而我们需要解决什么样的相机位姿最符合当前观测数据这样的问题。一种典型的方式是把它构建成一个优化问题,求解最优的 R, t,使得误差最小化。而估计、优化是需要进行迭代计算的。 但是,旋转矩阵自身是带有约束的(正交且行列式为 1)。它们作为优化变量时,会引入额外的约束,使优化变得困难。通过李群——李代数间的转换关系,我们希望把位姿估计变成无约束的优化问题,简化求解方式。所以引入了李群——李代数。 在优化和估计中,其实就是求最小误差,也就是求 的最小值.那么,就一定需要涉及到求导
的最小值.那么,就一定需要涉及到求导 来求最小值的问题.而BCH 公式以及近似是推理基础,最终通过对不引入额外的约束的李群——李代数进行求导或者扰动模型近似来完成优化问题所需要的求导部分.
来求最小值的问题.而BCH 公式以及近似是推理基础,最终通过对不引入额外的约束的李群——李代数进行求导或者扰动模型近似来完成优化问题所需要的求导部分.
4.1 李群李代数基础
三维旋转矩阵构成了特殊正交群 SO(3),而变换矩阵构成了特殊欧氏群 SE(3): 我们发现它们对加法是不封闭的。换句话说,对于任意两个旋转矩阵 R 1 , R 2 ,它们按照矩阵加法的定义,和不再是一个旋转矩阵。这两种矩阵并没有良好定义的加法,但是相对的,它们只有一种较好的运算:乘法。SO(3) 和 SE(3) 关于乘法是封闭的:
我们发现它们对加法是不封闭的。换句话说,对于任意两个旋转矩阵 R 1 , R 2 ,它们按照矩阵加法的定义,和不再是一个旋转矩阵。这两种矩阵并没有良好定义的加法,但是相对的,它们只有一种较好的运算:乘法。SO(3) 和 SE(3) 关于乘法是封闭的:
