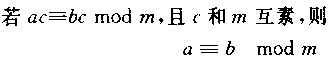同余与乘法逆元

2019-04-14 16:32发布

站内文章 / 模拟电子
13768 0 1742
  1. 同余：
    • 定义：设m≠0，若m∣a－b，即a－b＝km，则称a与b同余，余数为m。
    • 充要条件：a、b关于模m同余的充要条件是整数a和b被同一正整数m除时，有相同的余数。(a % m)=(b % m)意味a≡b (%m)
    • 性质：
      同余定理1
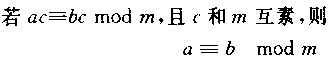
      这里写图片描述
    • 同余类：根据整数模n所得的余数，可以把整数分成n个等价类：[0],[1],…,[n-1]。
      包含整数的模n等价类为： [a]n={a+kn| k∈Z}。
    • 例题：求3406写成十进位数时的个位数.
      根据题意是要求a满足3406 ≡a（mod 10）
      显然32 ≡9 ≡－1 （mod 10），
      34 ≡1 （mod 10），
      从而3404 ≡1 （mod 10），
      因此3406 ≡ 3404 × 32 ≡9（mod 10）
      所以个位数是9.
  2. 模运算的运算规则
    • （1）(a + b) % p = (a % p + b % p) % p
    • （2）(a - b) % p = (a % p - b % p) % p
    • （3）(a * b) % p = (a % p * b % p) % p
    • （4）a ^ b % p = ((a % p)^b) % p
    • 结合律：
      （5）((a+b) % p + c) % p = (a + (b+c) % p) % p
      （6）((a*b) % p * c)% p = (a * (b*c) % p) % p
    • 交换律：
      （7）(a + b) % p = (b+a) % p
      （8）(a * b) % p = (b * a) % p
    • 分配律：
      （9）(a+b) % p = ( a % p + b % p ) % p
      （10) ((a +b)% p * c) % p = ((a * c) % p + (b * c) % p) % p
    • 重要定理：
      （11）若a≡b (% p)，则对于任意的c，都有(a + c) ≡ (b + c) (%p)
      （12）若a≡b (% p)，则对于任意的c，都有(a * c) ≡ (b * c)
      （13） 若a≡b (% p)，c≡d (% p)，则 (a + c) ≡ (b + d) (%p)，(a - c) ≡ (b - d) (%p)，
      (a * c) ≡ (b * d) (%p)，(a / c) ≡ (b / d) (%p)
  3. 乘法逆元：
    • 定义：
      满足a*k≡1 (mod p)的k值就是a关于p的乘法逆元。eg: 1=5*3-14 所以5关于模14的乘法逆元为3.
    • 应用：
      当我们要求 (a/b) mod P 的值时，如果 a 很大，无法直接求得a/b的值时，我们就可以使用乘法逆元。我们可以通过求b关于P的乘法逆元k，将a乘上k再模P，即(a%P*k)。其结果与(a/b) mod P等价。

热门文章