第一道 数电 有关逻辑函数设计的例题,个人认为很经典的一道 液位控制逻辑电路,刚刚开始写博客,可能排版和内容有些欠缺,希望大家多多包含。。

读完这道题目后,我想大多数刚学数电的人和我一样有种一时间找不到下手的感觉,那么就让 蒟蒻带你慢慢分析下,
这是这道题的图,,大家应该能很容易的看懂吧。。。

现在就照着这个图,把所有可能产生的情况都一一列举出来吧,这里我们引进水位量W(PS:因为水的单词是water), 当W大于 40时,Ms和Ml这两台发动机都不工作,故标记为 0, 0
当W大于 30而小于40时,Ms单独工作,故标记为 1 ,0 当W 大于20而小于30时,Ml单独工作,故标记为 0, 1
当W 小于20时, Ms和Ml都不工作,故标记为 0 , 0
于是乎,,得到了下面的这个逻辑真值表。。有点像 数模中的(0-1规划问题)

然后,我们在根据这个图开始进一步分析Ms和Ml的分布情况,,,先从Ms开始吧(本屌是冲着 SM去的)
那么,我们就将目光转接到第一行和第二行上, A = 1, B = 0. C = 0. Ms = 1. ML = 0. A = 0,B = 0, C= 0, MS = 0, ML = 0 又三者为0,并且现在是所说的逻辑代数,,立马想到A·B·C(为什么不想到A+B+C?因为在逻辑电路中,当输入变量大于等于2时,我们最好使用连乘积的形式) 又由A = 1, B = 0. C = 0. Ms = 1,,我们就可以假想这个关系式也是一个三个变量的连乘积确定的,故 A · B非·C非 ( 本屌水平有限,不会打那种在ABC上戴帽子的字符) 那么 综上结果就可以得到一个 Ms = A·B非·C非 + A·B·C 的式子了。。。
然后,我们继续按照这个思想 往下开始推到ML的式子 得到了 ML = A·B·C非 + A·B·C
(~ o ~)~zZ~ 就这样,,,第一个 液态控制电路问题 被我们 解决了,,,先别高兴的太早 还得画出这个逻辑电路图,,是用与和非什么的符号开始的,,,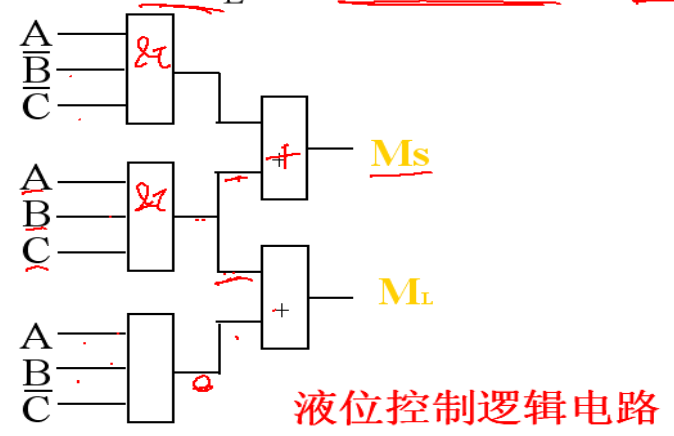
好了,,本屌的第一道逻辑设计题就讲到这里,,,没看懂的同学可以给我留言,有时间的话,我肯定会为大家耐心解答的。。。。

读完这道题目后,我想大多数刚学数电的人和我一样有种一时间找不到下手的感觉,那么就让 蒟蒻带你慢慢分析下,
这是这道题的图,,大家应该能很容易的看懂吧。。。

现在就照着这个图,把所有可能产生的情况都一一列举出来吧,这里我们引进水位量W(PS:因为水的单词是water), 当W大于 40时,Ms和Ml这两台发动机都不工作,故标记为 0, 0
当W大于 30而小于40时,Ms单独工作,故标记为 1 ,0 当W 大于20而小于30时,Ml单独工作,故标记为 0, 1
当W 小于20时, Ms和Ml都不工作,故标记为 0 , 0
于是乎,,得到了下面的这个逻辑真值表。。有点像 数模中的(0-1规划问题)

然后,我们在根据这个图开始进一步分析Ms和Ml的分布情况,,,先从Ms开始吧(本屌是冲着 SM去的)
那么,我们就将目光转接到第一行和第二行上, A = 1, B = 0. C = 0. Ms = 1. ML = 0. A = 0,B = 0, C= 0, MS = 0, ML = 0 又三者为0,并且现在是所说的逻辑代数,,立马想到A·B·C(为什么不想到A+B+C?因为在逻辑电路中,当输入变量大于等于2时,我们最好使用连乘积的形式) 又由A = 1, B = 0. C = 0. Ms = 1,,我们就可以假想这个关系式也是一个三个变量的连乘积确定的,故 A · B非·C非 ( 本屌水平有限,不会打那种在ABC上戴帽子的字符) 那么 综上结果就可以得到一个 Ms = A·B非·C非 + A·B·C 的式子了。。。
然后,我们继续按照这个思想 往下开始推到ML的式子 得到了 ML = A·B·C非 + A·B·C
(~ o ~)~zZ~ 就这样,,,第一个 液态控制电路问题 被我们 解决了,,,先别高兴的太早 还得画出这个逻辑电路图,,是用与和非什么的符号开始的,,,

好了,,本屌的第一道逻辑设计题就讲到这里,,,没看懂的同学可以给我留言,有时间的话,我肯定会为大家耐心解答的。。。。