1、复数1.1 复数的定义  图 1 - 1从解方程来看,方程在笛卡尔坐标系上应该都有解.但是象这样的方程(x² + 1 = 0)还是无解,因为没有一个实数的平方等于-1。在十六世纪,由于解方程的需要,人们开始引进一个新数,叫做虚数单位要解决这个方程 x² = -1 ,但是于任何实数的平方都是非负数矛盾,因此引入一个新的概念——复数。虚数的定义如下 i² = -1 ①i ^ 0 = 1 i ^ 1 = ii ^ 2 = −1i ^ 3 = i * i ^ 2 = −ii ^ 4 = i ^ 2 * i ^ 2 = 1i ^ 5 = i * i ^ 4 = i复数的集合是一个实数和一个虚数的和,形式如下:z = a + bi (a,b∈R, i ^ 2 = −1) ② 1.1.2 虚数的意义
图 1 - 1从解方程来看,方程在笛卡尔坐标系上应该都有解.但是象这样的方程(x² + 1 = 0)还是无解,因为没有一个实数的平方等于-1。在十六世纪,由于解方程的需要,人们开始引进一个新数,叫做虚数单位要解决这个方程 x² = -1 ,但是于任何实数的平方都是非负数矛盾,因此引入一个新的概念——复数。虚数的定义如下 i² = -1 ①i ^ 0 = 1 i ^ 1 = ii ^ 2 = −1i ^ 3 = i * i ^ 2 = −ii ^ 4 = i ^ 2 * i ^ 2 = 1i ^ 5 = i * i ^ 4 = i复数的集合是一个实数和一个虚数的和,形式如下:z = a + bi (a,b∈R, i ^ 2 = −1) ② 1.1.2 虚数的意义 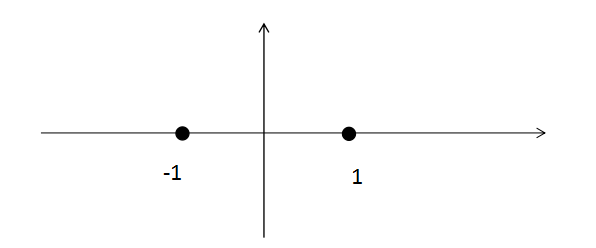 图 1 - 2假设现在点A(1, 0) 点B(-1, 0)那么A点经过 逆时针旋转90度两次 可以到达B点可得 1 * (逆时针旋转90度) * (逆时针旋转90度) = -1设i = (逆时针旋转90度) 则i * i = -1 也就是说i是旋转量实际上i ^ 1——i ^ 4 就是旋转360度 即虚数的周期 1.2 复数的运算
图 1 - 2假设现在点A(1, 0) 点B(-1, 0)那么A点经过 逆时针旋转90度两次 可以到达B点可得 1 * (逆时针旋转90度) * (逆时针旋转90度) = -1设i = (逆时针旋转90度) 则i * i = -1 也就是说i是旋转量实际上i ^ 1——i ^ 4 就是旋转360度 即虚数的周期 1.2 复数的运算 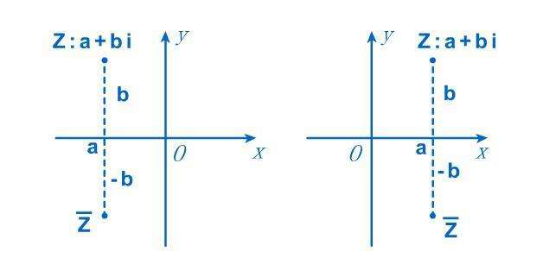 图 1 - 31.2.1 共轭复数如图(1-3)所示, 根据②可得复数可以由x轴(实数轴)与 y轴(虚数轴)确定唯一的一点,而实数相同,虚数向反的复数被称为共轭复数。如 z = a + bi 与 z’= a - bi ⑦ 1.2.2 复数的加、减、乘法运算根据定义② 复数 = 实数 + 虚数 则(a + bi) + (c + di) = (a + c) + (bi + di) = (a + c) + (b + d)i(a + bi) - (c + di) = (a + c) - (bi + di) = (a + c) - (b + d)i(a + bi) * (c + di) = ac + bci + adi + bdi * i根据定义① = (ac - bd) + (ad + bc)i 1.2.3 复数的向量与辐角
图 1 - 31.2.1 共轭复数如图(1-3)所示, 根据②可得复数可以由x轴(实数轴)与 y轴(虚数轴)确定唯一的一点,而实数相同,虚数向反的复数被称为共轭复数。如 z = a + bi 与 z’= a - bi ⑦ 1.2.2 复数的加、减、乘法运算根据定义② 复数 = 实数 + 虚数 则(a + bi) + (c + di) = (a + c) + (bi + di) = (a + c) + (b + d)i(a + bi) - (c + di) = (a + c) - (bi + di) = (a + c) - (b + d)i(a + bi) * (c + di) = ac + bci + adi + bdi * i根据定义① = (ac - bd) + (ad + bc)i 1.2.3 复数的向量与辐角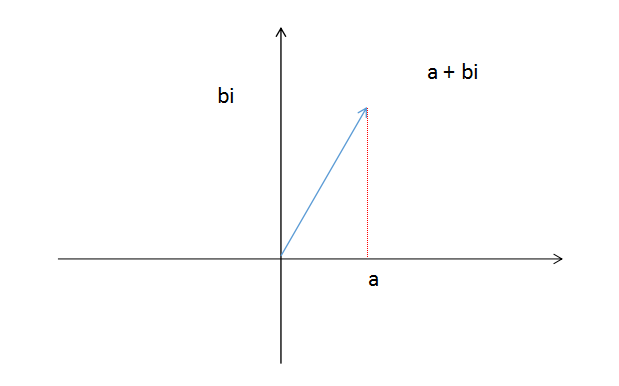 图 1 - 4向量: 既有绝对值大小又有方向的量线段的长度就是这个向量的绝对值(叫做这个向量的模)线段的方向(用箭头表示)就是这个向量的方向。求绝对值 |a| = (a * - a)^ 1/2a 与 -a 是数轴x上对称的两点而复数对称的两点分别为 a + bi 与 a - bi则 |a + bi| = [(a + bi)(a - bi)] ^ 1/2|a + bi| = ( a ^ 2 + b ^ 2) ^ 1/2 根据定义①这个向量与x轴构成的夹角就是复数辐角# tan(b/a) 1.2.4 复数的旋转
图 1 - 4向量: 既有绝对值大小又有方向的量线段的长度就是这个向量的绝对值(叫做这个向量的模)线段的方向(用箭头表示)就是这个向量的方向。求绝对值 |a| = (a * - a)^ 1/2a 与 -a 是数轴x上对称的两点而复数对称的两点分别为 a + bi 与 a - bi则 |a + bi| = [(a + bi)(a - bi)] ^ 1/2|a + bi| = ( a ^ 2 + b ^ 2) ^ 1/2 根据定义①这个向量与x轴构成的夹角就是复数辐角# tan(b/a) 1.2.4 复数的旋转 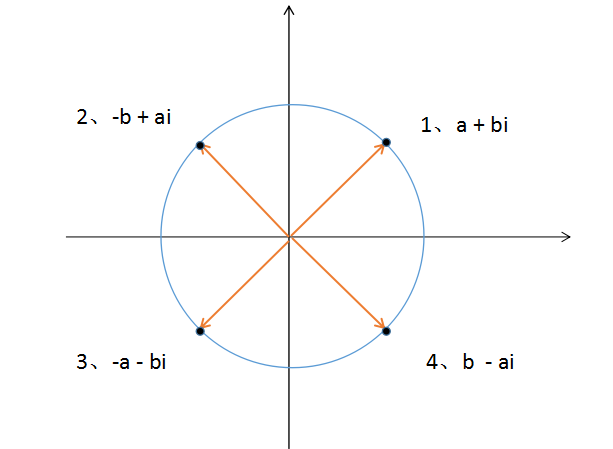 图 1 - 5在数轴上任何取一点 a + bi 连续与i 相乘4次 根据定义① 可得,则几个数分别为:1、 a + bi2、 -b + ai3、 -a - bi4、 b - aib - ai 乘以 i 又回到了 a + bi 实际上乘以 i 是复数 a + bi (a = 0, b = 1)的特殊情况那么一般情况的复数相乘又代表什么呢?定义以下复数(n为复数向量的模)p = n1(cosA + i * sinA)q = n2(cosB + i * sinB)则 pq = n1 * n2(cosA + i * sinA)(cosB + i * sinB) = n1 * n2[(cosAcosB - sinAsinB) + i(sinAcosB + cosAsinB)] = n1 * n2[cos(A + B) + isin(A + B)]可得复数相乘 1、积的模 = 两复数模的积 (n1 * n2 = n1 * n2) 2、积的辐角 = 两复数辐角的和 ( A + B = A + B)复数的相乘会使复数向量的模增加或减小,并且旋转改变该向量的方向而旋转后的角度为原复数辐角的和 ④根据④容易用复数求得方向
图 1 - 5在数轴上任何取一点 a + bi 连续与i 相乘4次 根据定义① 可得,则几个数分别为:1、 a + bi2、 -b + ai3、 -a - bi4、 b - aib - ai 乘以 i 又回到了 a + bi 实际上乘以 i 是复数 a + bi (a = 0, b = 1)的特殊情况那么一般情况的复数相乘又代表什么呢?定义以下复数(n为复数向量的模)p = n1(cosA + i * sinA)q = n2(cosB + i * sinB)则 pq = n1 * n2(cosA + i * sinA)(cosB + i * sinB) = n1 * n2[(cosAcosB - sinAsinB) + i(sinAcosB + cosAsinB)] = n1 * n2[cos(A + B) + isin(A + B)]可得复数相乘 1、积的模 = 两复数模的积 (n1 * n2 = n1 * n2) 2、积的辐角 = 两复数辐角的和 ( A + B = A + B)复数的相乘会使复数向量的模增加或减小,并且旋转改变该向量的方向而旋转后的角度为原复数辐角的和 ④根据④容易用复数求得方向 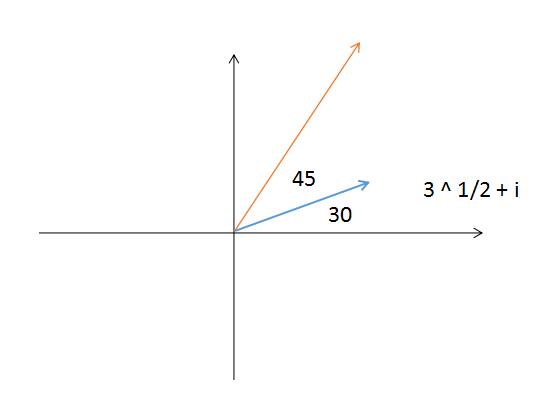 图 1 - 6如图(1-6) 在海航上,船原来的坐标是(3 ^ 1/2, i),经过45度的旋转后现在船的方向是多少复数相乘方向不考虑模的大小,因此辐角45度可以设复数为1 + i则 (3 ^ 1/2 + i)(1 + i) = (3 ^ 1/2 - 1) + (3 ^ 1/2 + 1)i即为此时的方向,此时的辐角为(3 ^ 1/2 + 1) / (3 ^ 1/2 - 1) = tan75 2、 四元数的定义2.1 四元数的记法
图 1 - 6如图(1-6) 在海航上,船原来的坐标是(3 ^ 1/2, i),经过45度的旋转后现在船的方向是多少复数相乘方向不考虑模的大小,因此辐角45度可以设复数为1 + i则 (3 ^ 1/2 + i)(1 + i) = (3 ^ 1/2 - 1) + (3 ^ 1/2 + 1)i即为此时的方向,此时的辐角为(3 ^ 1/2 + 1) / (3 ^ 1/2 - 1) = tan75 2、 四元数的定义2.1 四元数的记法 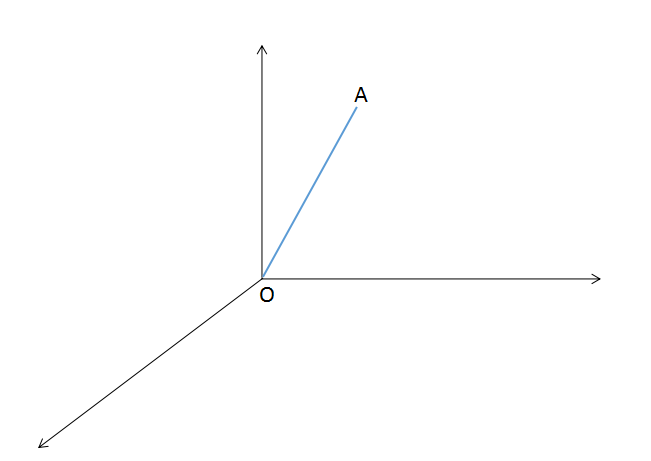 图 2 - 1欧拉证明了 一个旋转序列等价于单个旋转。想象一下,你有一根木棒,其中一端固定在一个地方,通过任意移动木棒,可以达到任意的角度(如图 2 - 1)因此, 3D空间中任意角位移都可以表示成绕单一轴的单一旋转。四元数的一般形式:q = w + xi + yj + zk w,x,y,z∈R四元数的简写形式:q = [cosA, sinA * n] ⑥ = [cosA, (sinA * n_x, sinA * n_y, sinA * n_z)]w == 木棒的长度 (i, j, k)相当于三维空间的坐标 2.1.2 复数与笛卡尔乘积
图 2 - 1欧拉证明了 一个旋转序列等价于单个旋转。想象一下,你有一根木棒,其中一端固定在一个地方,通过任意移动木棒,可以达到任意的角度(如图 2 - 1)因此, 3D空间中任意角位移都可以表示成绕单一轴的单一旋转。四元数的一般形式:q = w + xi + yj + zk w,x,y,z∈R四元数的简写形式:q = [cosA, sinA * n] ⑥ = [cosA, (sinA * n_x, sinA * n_y, sinA * n_z)]w == 木棒的长度 (i, j, k)相当于三维空间的坐标 2.1.2 复数与笛卡尔乘积 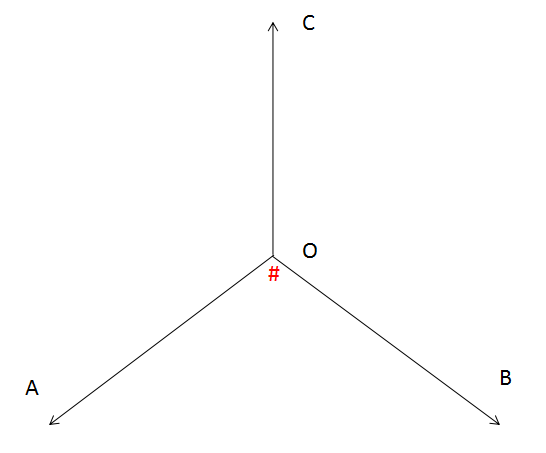 图 2 - 2设向量OA = A, 向量OB = B, 向量OC = C向量叉乘公式 C = A × B = |A||B|sin# #代表向量A、B之间的夹角 ④
图 2 - 2设向量OA = A, 向量OB = B, 向量OC = C向量叉乘公式 C = A × B = |A||B|sin# #代表向量A、B之间的夹角 ④ 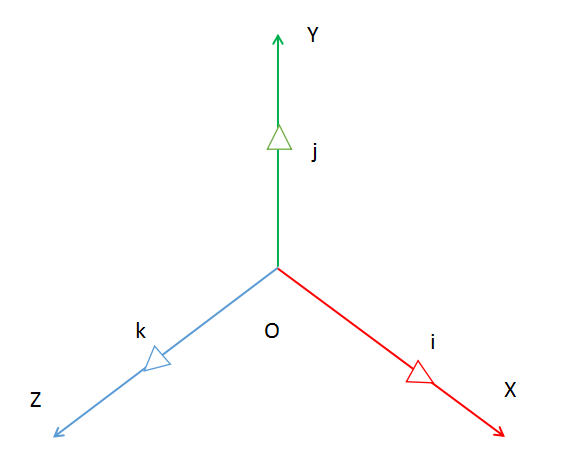 图 2 - 3如图(2 - 3) 假设i代表x轴的正方向, j代表y轴正方向, k代表z轴正方向根据定义④可得 i × j = k, j × k = i k × i = j, j × i = -k i × k = -j, i × k = -j ⑤可由右手定理判断正反符号,如计算i × j第一步 将右手的4个指头指向第一个数i第二步 将右手向j的方向转第三步 此时拇指 指向k的正方向 则i × j = k如计算j × i第一步 将右手的4个指头指向第一个数j第二步 将右手向i的方向转第三步 此时拇指 指向k的负方向(正方向的反方向) 则j × i = -k 2.1.3 负四元数与单位四元数设四元数q = [w, (x, y, z)], -q = [-w, (-x, -y, -z)]设点A(x, y, z), B(-x, -y, -z), 向量_OA = (x, y, z), 向量_OB = (-x, -y, -z)_OA = -_OB,则A,O,B三点共线,也就是说q与 -q旋转轴相同,又因为对于旋转轴,长度可以忽略不计,则对于四元数q = -q在几何上,单位四元数的定义为乘以任意四元数q,得到的结果为q。如图2-1,将这条线段绕多少度可以变回原来的样子,显然是360度整数倍数,又根据 ⑥ 可得单位四元数为q = [cos(360n), sin(360n)n] = [1, 0] = [-1, 0] 2.1.4 四元数的模||q|| = ||[w, (x, y, z)]|| = (w ^ 2 + x ^ 2 + y ^ 2 + z ^ 2) ^ 1/2= ||[w, v]|| = (w ^ 2 + ||v|| ^ 2) ^ 1/2 根据⑥,代入A和n可得:||q|| = ||[w, v]|| = (cosA ^ 2 + (sinA||n||) ^ 2) ^ 1/2n为单位向量,则:||q|| = (cosA ^ 2 + sinA ^ 2) ^ 1/2 = 1可得单位四元数的模为1 2.1.5 四元数的叉乘q = [w1, (x1, y1, z1)]p = [w2, (x2, y2, z3)]pq = (w1w2 − x1x2 − y1y2 − z1z2)+(w1x2 + w2x1 + y1z2 − y2z1)i+(w1y2 + w2y1 + z1x2 − z2x1)j+(w1z2 + w2z1 + x1y2 − x2y1)k = (w1w2 − x1x2 − y1y2 − z1z2)+ w1(x2i + y2j + z2k) + w2(x1i + y1j + z1k)+ (y1z2 - y2z1)i + (z1x2 - z2x1)j + (x1y2 - x2y1)k 设A = (x2i + y2j + z2k),B = (x1i + y1j + z1k)又根据:1、向量的点积 A ▪ B = x1x2(i * i) + y1y2(j * j) + z1z2(k * k)= x1x2 + y1y2 + z1z2 (向量的点积是标量 此处i = j = k = 1)2、 向量的叉乘 A × B = x1y1(i * i) + x1y2(i * j) + x1z2(i * k) + y1x2(j * i) + y1y2(j * j) + y1z2(j * k) + z1x2(k * j) + z1y2(k * j) + z1z2(k * k)在根据⑤ 化简可得 A × B = (y1z2 - y2z1)i + (z1x2 - z2x1)j + (x1y2 - x2y1)k 则pq = (w1w2 - A ▪ B) + (w1A + w2B + A × B)= [w1w2 - A ▪ B, w1A + w2B + A × B] ⑧ 结论:四元数乘积的模等于模的乘积 ⑨——> 两个单位四元数相乘的结果还是单位四元数假设p, q分别为单位四元数则p = [1, 0], q = [1, 0]||pq|| = ||1 + 0 + 0 + 0|| = ||1|| = 1||p|| * ||q|| = ||1|| * ||1|| = 1 2.1.7 四元数共轭和逆根据⑦可得q’ = [w, v]’= [w, v’]= [w, (-x, -y, -z)] ⑩ 四元数的逆为 q ^ -1, 定义为四元数的共轭除以他的模q ^ -1 = q’/ ||q|| 结论:(ab) ^ -1 = (b^-1)(a^-1)设 a = [w1, v1] b = [w2, v2]则 (ab)^-1 = (ab)’/ ||ab||根据⑧ (ab) = [w1w2 - v1 ▪ v2, w1v1 + w2v2 + v1 × v2]根据⑩ (ab)’ = [w1w2 - v1 ▪ v2, -(w1v1 + w2v2 + v1 × v2)]b’ = [w2, -v2]a’ = [w1, -v1]根据⑤⑧可得b’a’ = [w1w2 - v1 ▪ v2, -(w1v1 + w2v2 + v1 × v2)](b^-1)(a^-1) = b’a’/ ||b||||a||根据⑨ ||ab|| = ||b||||a||又因为 (ab)’ = b’a’则(ab) ^ -1 = (b^-1)(a^-1)成立可得 (q1q2q3...qn) ^ -1 = (qn)^-1...(q2^-1)(q1^-1)即四元数的乘积的逆等于各个四元数的逆以相反顺序相乘 ⑪ 2.1.8 四元数的旋转根据④可得 复数的相乘可以表示2D上的旋转那么四元数的相乘是否可以表示3D上的旋转呢?就如同三维上的点(x, y, z) 当z = 0时可以表示为二维上的点同理将四维上的点[w, v] 当w = 0时可以表示三维上的点设 p = [0, (ai, bj, ck)] q = [w1, (x1i, y1j, z1k)] (表示旋转轴) q^-1 = [w1, -(x1, y1, z1)]qp = [-(ax1 + by1 + cz1), (aw1 + cy1 - bz1)i, (bw1 + az1 - cx1)j, (cw1 + ay1 - bx1)k] pq^-1 = [(ax1 + bx1 + cz1), (aw1 - bz1 + cy1)i, (bw1 - cx1 + az1)j, (cw1 - bx1 + ay1)k]观察可得qp 与 pq^-1的第四维互为相反数,而在三维坐标上的点相同也就是说都是沿相同的方向转过了相同的角度。又因为他们的模相同则qp 与 pq^-1的几何意义是两个相同的旋转而qp 可以通过复数q与复数p相乘得到pq^-1可以通过复数q^-1与复数p相乘得到将向量q与q^-1平移到圆点,如图(2-4)所示
图 2 - 3如图(2 - 3) 假设i代表x轴的正方向, j代表y轴正方向, k代表z轴正方向根据定义④可得 i × j = k, j × k = i k × i = j, j × i = -k i × k = -j, i × k = -j ⑤可由右手定理判断正反符号,如计算i × j第一步 将右手的4个指头指向第一个数i第二步 将右手向j的方向转第三步 此时拇指 指向k的正方向 则i × j = k如计算j × i第一步 将右手的4个指头指向第一个数j第二步 将右手向i的方向转第三步 此时拇指 指向k的负方向(正方向的反方向) 则j × i = -k 2.1.3 负四元数与单位四元数设四元数q = [w, (x, y, z)], -q = [-w, (-x, -y, -z)]设点A(x, y, z), B(-x, -y, -z), 向量_OA = (x, y, z), 向量_OB = (-x, -y, -z)_OA = -_OB,则A,O,B三点共线,也就是说q与 -q旋转轴相同,又因为对于旋转轴,长度可以忽略不计,则对于四元数q = -q在几何上,单位四元数的定义为乘以任意四元数q,得到的结果为q。如图2-1,将这条线段绕多少度可以变回原来的样子,显然是360度整数倍数,又根据 ⑥ 可得单位四元数为q = [cos(360n), sin(360n)n] = [1, 0] = [-1, 0] 2.1.4 四元数的模||q|| = ||[w, (x, y, z)]|| = (w ^ 2 + x ^ 2 + y ^ 2 + z ^ 2) ^ 1/2= ||[w, v]|| = (w ^ 2 + ||v|| ^ 2) ^ 1/2 根据⑥,代入A和n可得:||q|| = ||[w, v]|| = (cosA ^ 2 + (sinA||n||) ^ 2) ^ 1/2n为单位向量,则:||q|| = (cosA ^ 2 + sinA ^ 2) ^ 1/2 = 1可得单位四元数的模为1 2.1.5 四元数的叉乘q = [w1, (x1, y1, z1)]p = [w2, (x2, y2, z3)]pq = (w1w2 − x1x2 − y1y2 − z1z2)+(w1x2 + w2x1 + y1z2 − y2z1)i+(w1y2 + w2y1 + z1x2 − z2x1)j+(w1z2 + w2z1 + x1y2 − x2y1)k = (w1w2 − x1x2 − y1y2 − z1z2)+ w1(x2i + y2j + z2k) + w2(x1i + y1j + z1k)+ (y1z2 - y2z1)i + (z1x2 - z2x1)j + (x1y2 - x2y1)k 设A = (x2i + y2j + z2k),B = (x1i + y1j + z1k)又根据:1、向量的点积 A ▪ B = x1x2(i * i) + y1y2(j * j) + z1z2(k * k)= x1x2 + y1y2 + z1z2 (向量的点积是标量 此处i = j = k = 1)2、 向量的叉乘 A × B = x1y1(i * i) + x1y2(i * j) + x1z2(i * k) + y1x2(j * i) + y1y2(j * j) + y1z2(j * k) + z1x2(k * j) + z1y2(k * j) + z1z2(k * k)在根据⑤ 化简可得 A × B = (y1z2 - y2z1)i + (z1x2 - z2x1)j + (x1y2 - x2y1)k 则pq = (w1w2 - A ▪ B) + (w1A + w2B + A × B)= [w1w2 - A ▪ B, w1A + w2B + A × B] ⑧ 结论:四元数乘积的模等于模的乘积 ⑨——> 两个单位四元数相乘的结果还是单位四元数假设p, q分别为单位四元数则p = [1, 0], q = [1, 0]||pq|| = ||1 + 0 + 0 + 0|| = ||1|| = 1||p|| * ||q|| = ||1|| * ||1|| = 1 2.1.7 四元数共轭和逆根据⑦可得q’ = [w, v]’= [w, v’]= [w, (-x, -y, -z)] ⑩ 四元数的逆为 q ^ -1, 定义为四元数的共轭除以他的模q ^ -1 = q’/ ||q|| 结论:(ab) ^ -1 = (b^-1)(a^-1)设 a = [w1, v1] b = [w2, v2]则 (ab)^-1 = (ab)’/ ||ab||根据⑧ (ab) = [w1w2 - v1 ▪ v2, w1v1 + w2v2 + v1 × v2]根据⑩ (ab)’ = [w1w2 - v1 ▪ v2, -(w1v1 + w2v2 + v1 × v2)]b’ = [w2, -v2]a’ = [w1, -v1]根据⑤⑧可得b’a’ = [w1w2 - v1 ▪ v2, -(w1v1 + w2v2 + v1 × v2)](b^-1)(a^-1) = b’a’/ ||b||||a||根据⑨ ||ab|| = ||b||||a||又因为 (ab)’ = b’a’则(ab) ^ -1 = (b^-1)(a^-1)成立可得 (q1q2q3...qn) ^ -1 = (qn)^-1...(q2^-1)(q1^-1)即四元数的乘积的逆等于各个四元数的逆以相反顺序相乘 ⑪ 2.1.8 四元数的旋转根据④可得 复数的相乘可以表示2D上的旋转那么四元数的相乘是否可以表示3D上的旋转呢?就如同三维上的点(x, y, z) 当z = 0时可以表示为二维上的点同理将四维上的点[w, v] 当w = 0时可以表示三维上的点设 p = [0, (ai, bj, ck)] q = [w1, (x1i, y1j, z1k)] (表示旋转轴) q^-1 = [w1, -(x1, y1, z1)]qp = [-(ax1 + by1 + cz1), (aw1 + cy1 - bz1)i, (bw1 + az1 - cx1)j, (cw1 + ay1 - bx1)k] pq^-1 = [(ax1 + bx1 + cz1), (aw1 - bz1 + cy1)i, (bw1 - cx1 + az1)j, (cw1 - bx1 + ay1)k]观察可得qp 与 pq^-1的第四维互为相反数,而在三维坐标上的点相同也就是说都是沿相同的方向转过了相同的角度。又因为他们的模相同则qp 与 pq^-1的几何意义是两个相同的旋转而qp 可以通过复数q与复数p相乘得到pq^-1可以通过复数q^-1与复数p相乘得到将向量q与q^-1平移到圆点,如图(2-4)所示 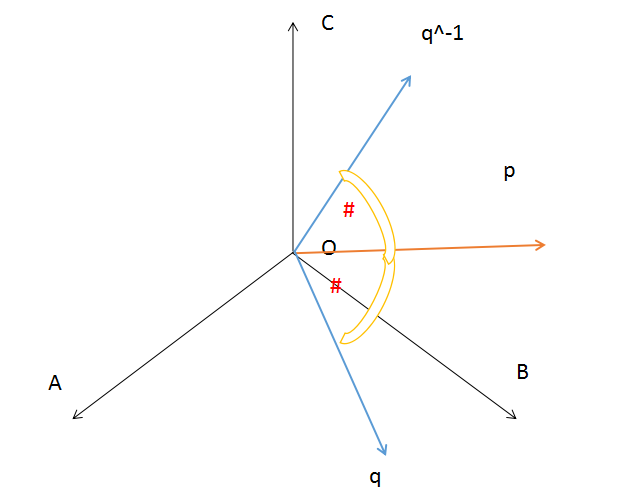 图 2 - 4第一次旋转为qp第二次旋转为(qp)q^-1设旋转的结果后为p’ 则p’ = qpq^-1 ⑫因为是旋转了两次,因此需要用四元数计算旋转的时候,角度是 (2 * #) / 2 = 2即按照目标角度的一半来计算 (2 * #)的几何意义为目标角度 3、 四元数的插值3.1 普通线性插值
图 2 - 4第一次旋转为qp第二次旋转为(qp)q^-1设旋转的结果后为p’ 则p’ = qpq^-1 ⑫因为是旋转了两次,因此需要用四元数计算旋转的时候,角度是 (2 * #) / 2 = 2即按照目标角度的一半来计算 (2 * #)的几何意义为目标角度 3、 四元数的插值3.1 普通线性插值 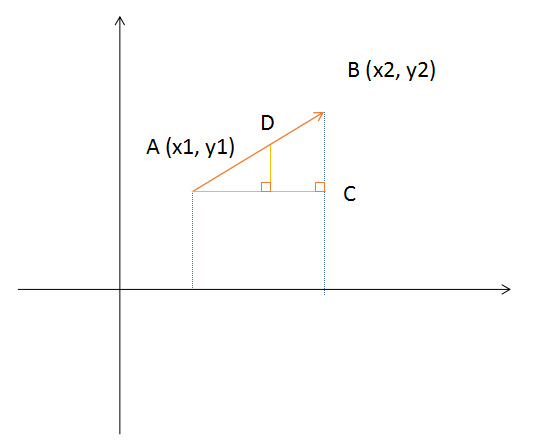 图 3 - 1如图(3-1),在一条直线AB上插入任意一个值,我们需要的是点D的坐标。如图所示过A、B点分别做x轴的垂线。分别交予x轴与点E、F。过A点做与BF的垂线,交于点C,连接AC。在AB上任意取一点D,过D点做与AC的垂线,交于点M。设D(x0, y0)则x0 - x1 = AM显然∠BAC = ∠DAMtan∠BAC = BC / ACtan∠DAM = DM / AM则 BC / AC = DM / AMAC = x2 - x1, BC = y2 - y1DM = (y2 - y1 / x2 - x1 )(x0 - x1)y0 = AE + DM = y1 + (y2 - y1 / x2 - x1 )(x0 - x1)即 y0 = y1 + (y2 - y1 / x2 - x1 )(x0 - x1)
图 3 - 1如图(3-1),在一条直线AB上插入任意一个值,我们需要的是点D的坐标。如图所示过A、B点分别做x轴的垂线。分别交予x轴与点E、F。过A点做与BF的垂线,交于点C,连接AC。在AB上任意取一点D,过D点做与AC的垂线,交于点M。设D(x0, y0)则x0 - x1 = AM显然∠BAC = ∠DAMtan∠BAC = BC / ACtan∠DAM = DM / AM则 BC / AC = DM / AMAC = x2 - x1, BC = y2 - y1DM = (y2 - y1 / x2 - x1 )(x0 - x1)y0 = AE + DM = y1 + (y2 - y1 / x2 - x1 )(x0 - x1)即 y0 = y1 + (y2 - y1 / x2 - x1 )(x0 - x1) 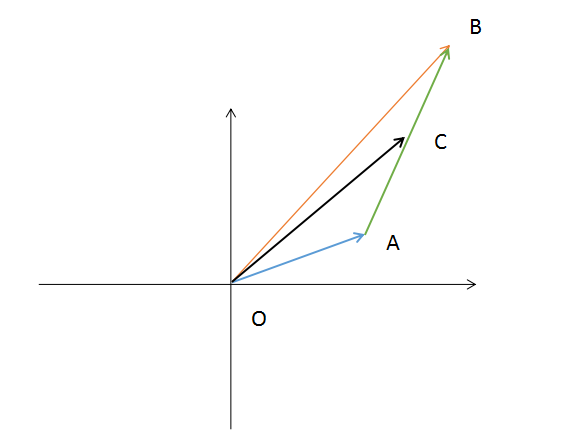 图 3 - 2在平面上任意取A点与B点,做向量_OA与向量_OB。连接AB,做向量_AB。在AB上任意取一点C,做向量_OC。则1. _OA + _AB = _OB, _OA + _AC = _OC因为点C在直线AB上,则_AC 与 _AB共线, 设_AC = t _AB则2. _OC = _OA + t_AB标准线性插值公式:lerp(a0, a1, t) = a0 + t△a △a = a1 - a0 ⑬设a0 = _OA, a1 = _OB 根据1与2可得_OC = a0 + t△a △a = a1 - a0 3.2 四元数插值——slerp
图 3 - 2在平面上任意取A点与B点,做向量_OA与向量_OB。连接AB,做向量_AB。在AB上任意取一点C,做向量_OC。则1. _OA + _AB = _OB, _OA + _AC = _OC因为点C在直线AB上,则_AC 与 _AB共线, 设_AC = t _AB则2. _OC = _OA + t_AB标准线性插值公式:lerp(a0, a1, t) = a0 + t△a △a = a1 - a0 ⑬设a0 = _OA, a1 = _OB 根据1与2可得_OC = a0 + t△a △a = a1 - a0 3.2 四元数插值——slerp 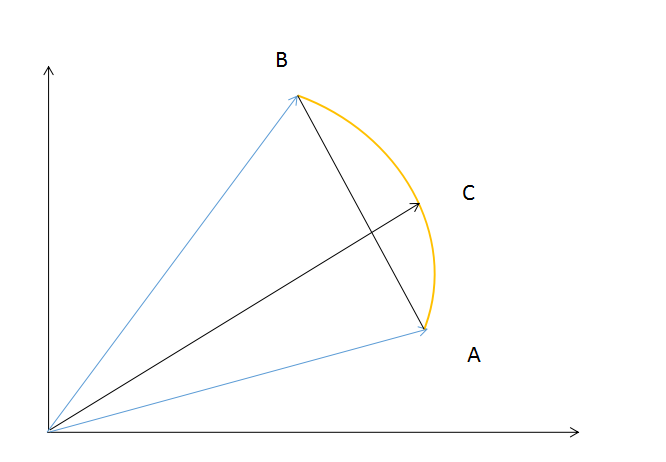 图 3 - 3在球形体中插值,显然轨迹是弧形的,如图(3-3)所示。显然点C在弧AB的运动过程中,线段OC的长度的不变的而普通的线性插值_OC的长度是会改变的, 如图(3-2)
图 3 - 3在球形体中插值,显然轨迹是弧形的,如图(3-3)所示。显然点C在弧AB的运动过程中,线段OC的长度的不变的而普通的线性插值_OC的长度是会改变的, 如图(3-2) 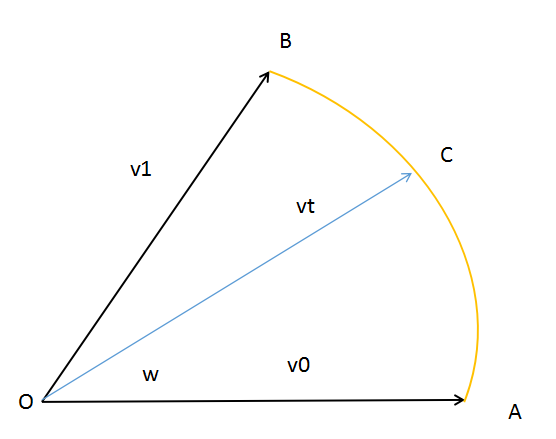 图 3 - 4sleap的基本思想是 沿4D球面上连接的两个四元数的弧插值(球面插值)把这种思想表现在平面上如图(3-4),设两个2D向量_OA与_OB,我们需要计算_OC,设w是_OA到_OB弧所截的角为了方便计算 设v0 = _OA, v1 = _OB, vt = _OC将vt表示成v0与v1的线性组合: vt = kovo + k1v1
图 3 - 4sleap的基本思想是 沿4D球面上连接的两个四元数的弧插值(球面插值)把这种思想表现在平面上如图(3-4),设两个2D向量_OA与_OB,我们需要计算_OC,设w是_OA到_OB弧所截的角为了方便计算 设v0 = _OA, v1 = _OB, vt = _OC将vt表示成v0与v1的线性组合: vt = kovo + k1v1 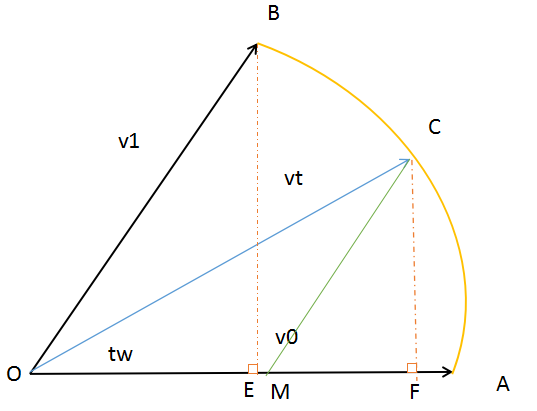 图 3 - 5过C点做OB的平行线,交OA与点M。分别过点B与点C做于OA的垂线,分别交线段OA于点E、M。易得△BOE与△CMF是相似三角形则 OB / BE = CM / CFOB = |v1|, BE = OB * sinw = |v1|sinwCM = k1|v1|, CF = OC*sintw = |vt|sintw = |v1|sintw (线段OC与OB长度相同,则|vt| = |v1|)代入可得: k1 = sintw / sinw ⒂
图 3 - 5过C点做OB的平行线,交OA与点M。分别过点B与点C做于OA的垂线,分别交线段OA于点E、M。易得△BOE与△CMF是相似三角形则 OB / BE = CM / CFOB = |v1|, BE = OB * sinw = |v1|sinwCM = k1|v1|, CF = OC*sintw = |vt|sintw = |v1|sintw (线段OC与OB长度相同,则|vt| = |v1|)代入可得: k1 = sintw / sinw ⒂ 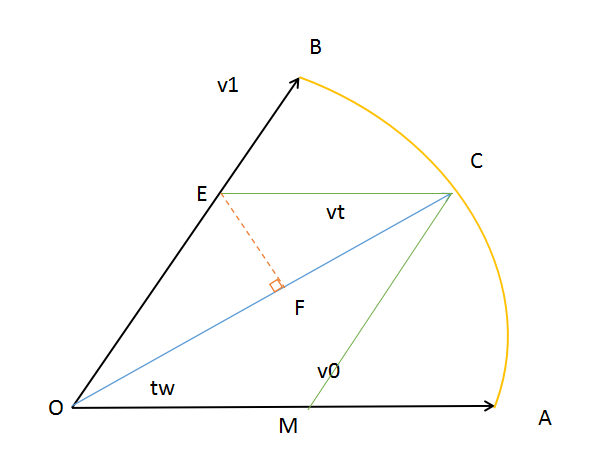 图 3 - 6 过C点做于OA的平行线,交OB于点E。过点E做OC的垂线,交OC于点F。易得_OE = _MC = k1v1, _EC = _OM = k0v0∠EOC = (1-t)w, ∠ECO = W线段EF = OE sin∠EOC = EC sin∠ECO则 k1|v1| sin((1-t)w) = k0|v0| sinw = k0|v1|sinw根据⒂可得: k0 = sin(1 - t)w / sinw ⒃将⒂⒃代入到 vt = kovo + k1v1可得vt = (sin(1 - t)w / sinw )vo + ( sintw / sinw)v1将同样的思想扩展到四元数,重写slerp可得:slerp(q0, q1, t) = (sin(1 - t)w / sinw )q0 + ( sintw / sinw)q1而w, 可以计算q1和q2的点积从而得出角度w:cosw = q1▪q2 / |q1||q2| 这样的作法会产生两个问题:
图 3 - 6 过C点做于OA的平行线,交OB于点E。过点E做OC的垂线,交OC于点F。易得_OE = _MC = k1v1, _EC = _OM = k0v0∠EOC = (1-t)w, ∠ECO = W线段EF = OE sin∠EOC = EC sin∠ECO则 k1|v1| sin((1-t)w) = k0|v0| sinw = k0|v1|sinw根据⒂可得: k0 = sin(1 - t)w / sinw ⒃将⒂⒃代入到 vt = kovo + k1v1可得vt = (sin(1 - t)w / sinw )vo + ( sintw / sinw)v1将同样的思想扩展到四元数,重写slerp可得:slerp(q0, q1, t) = (sin(1 - t)w / sinw )q0 + ( sintw / sinw)q1而w, 可以计算q1和q2的点积从而得出角度w:cosw = q1▪q2 / |q1||q2| 这样的作法会产生两个问题: 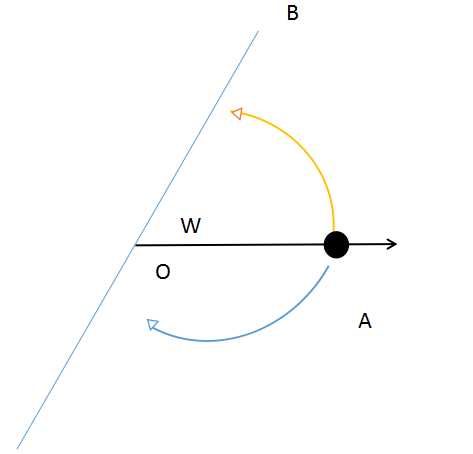 图 3 - 71. 可能会绕远路,将点A旋转到OB旋转轴,可以顺时针旋转也可以逆时针旋转。设∠BOA = w, 显然当w小于90度的时候,顺时针旋转所需要的路径较短,而当w大于90度的时候,逆时针旋转所需要的路径较短。首先我们需要确定w是否大于90度,可以使用:cosw = q1▪q2 / |q1||q2| 0 < w < 180因为 |q1||q2| > 0恒成立所以实际上需要计算的是q1▪q2 当q1▪q2 > 0的时候, cosw > 0 w < 90当q1▪q2 < 0的时候, cosw < 0 w > 90确定了角度之后,我们需要的是按顺时针还是逆时针旋转而四元数代表旋转轴的时候q = -q我们可以将其中一个四元数取反,总结:q1▪q2 > 0时, 旋转为q1q2q1▪q2 <= 0时, 旋转为(-q1)q2或(-q2) 2. 当w较小的时候,sinw ——> 0,sin(1 - t)w ——> 1则(sin(1 - t)w / sinw )q0 ——> ∞计算机没有真正的∞,所以我们需要确定一个sinw的范围,如当sinw < 0.0001的时候sinw = 0.0001。 4、 个人说明本文参考于《3D数学基础:图形与游戏开发》,文中内容属于个人(萌新)理解,可能会出现一些错误,欢迎大佬指正,本文仅供参考。
图 3 - 71. 可能会绕远路,将点A旋转到OB旋转轴,可以顺时针旋转也可以逆时针旋转。设∠BOA = w, 显然当w小于90度的时候,顺时针旋转所需要的路径较短,而当w大于90度的时候,逆时针旋转所需要的路径较短。首先我们需要确定w是否大于90度,可以使用:cosw = q1▪q2 / |q1||q2| 0 < w < 180因为 |q1||q2| > 0恒成立所以实际上需要计算的是q1▪q2 当q1▪q2 > 0的时候, cosw > 0 w < 90当q1▪q2 < 0的时候, cosw < 0 w > 90确定了角度之后,我们需要的是按顺时针还是逆时针旋转而四元数代表旋转轴的时候q = -q我们可以将其中一个四元数取反,总结:q1▪q2 > 0时, 旋转为q1q2q1▪q2 <= 0时, 旋转为(-q1)q2或(-q2) 2. 当w较小的时候,sinw ——> 0,sin(1 - t)w ——> 1则(sin(1 - t)w / sinw )q0 ——> ∞计算机没有真正的∞,所以我们需要确定一个sinw的范围,如当sinw < 0.0001的时候sinw = 0.0001。 4、 个人说明本文参考于《3D数学基础:图形与游戏开发》,文中内容属于个人(萌新)理解,可能会出现一些错误,欢迎大佬指正,本文仅供参考。
 图 1 - 1从解方程来看,方程在笛卡尔坐标系上应该都有解.但是象这样的方程(x² + 1 = 0)还是无解,因为没有一个实数的平方等于-1。在十六世纪,由于解方程的需要,人们开始引进一个新数,叫做虚数单位要解决这个方程 x² = -1 ,但是于任何实数的平方都是非负数矛盾,因此引入一个新的概念——复数。虚数的定义如下 i² = -1 ①i ^ 0 = 1 i ^ 1 = ii ^ 2 = −1i ^ 3 = i * i ^ 2 = −ii ^ 4 = i ^ 2 * i ^ 2 = 1i ^ 5 = i * i ^ 4 = i复数的集合是一个实数和一个虚数的和,形式如下:z = a + bi (a,b∈R, i ^ 2 = −1) ② 1.1.2 虚数的意义
图 1 - 1从解方程来看,方程在笛卡尔坐标系上应该都有解.但是象这样的方程(x² + 1 = 0)还是无解,因为没有一个实数的平方等于-1。在十六世纪,由于解方程的需要,人们开始引进一个新数,叫做虚数单位要解决这个方程 x² = -1 ,但是于任何实数的平方都是非负数矛盾,因此引入一个新的概念——复数。虚数的定义如下 i² = -1 ①i ^ 0 = 1 i ^ 1 = ii ^ 2 = −1i ^ 3 = i * i ^ 2 = −ii ^ 4 = i ^ 2 * i ^ 2 = 1i ^ 5 = i * i ^ 4 = i复数的集合是一个实数和一个虚数的和,形式如下:z = a + bi (a,b∈R, i ^ 2 = −1) ② 1.1.2 虚数的意义  图 1 - 2假设现在点A(1, 0) 点B(-1, 0)那么A点经过 逆时针旋转90度两次 可以到达B点可得 1 * (逆时针旋转90度) * (逆时针旋转90度) = -1设i = (逆时针旋转90度) 则i * i = -1 也就是说i是旋转量实际上i ^ 1——i ^ 4 就是旋转360度 即虚数的周期 1.2 复数的运算
图 1 - 2假设现在点A(1, 0) 点B(-1, 0)那么A点经过 逆时针旋转90度两次 可以到达B点可得 1 * (逆时针旋转90度) * (逆时针旋转90度) = -1设i = (逆时针旋转90度) 则i * i = -1 也就是说i是旋转量实际上i ^ 1——i ^ 4 就是旋转360度 即虚数的周期 1.2 复数的运算  图 1 - 31.2.1 共轭复数如图(1-3)所示, 根据②可得复数可以由x轴(实数轴)与 y轴(虚数轴)确定唯一的一点,而实数相同,虚数向反的复数被称为共轭复数。如 z = a + bi 与 z’= a - bi ⑦ 1.2.2 复数的加、减、乘法运算根据定义② 复数 = 实数 + 虚数 则(a + bi) + (c + di) = (a + c) + (bi + di) = (a + c) + (b + d)i(a + bi) - (c + di) = (a + c) - (bi + di) = (a + c) - (b + d)i(a + bi) * (c + di) = ac + bci + adi + bdi * i根据定义① = (ac - bd) + (ad + bc)i 1.2.3 复数的向量与辐角
图 1 - 31.2.1 共轭复数如图(1-3)所示, 根据②可得复数可以由x轴(实数轴)与 y轴(虚数轴)确定唯一的一点,而实数相同,虚数向反的复数被称为共轭复数。如 z = a + bi 与 z’= a - bi ⑦ 1.2.2 复数的加、减、乘法运算根据定义② 复数 = 实数 + 虚数 则(a + bi) + (c + di) = (a + c) + (bi + di) = (a + c) + (b + d)i(a + bi) - (c + di) = (a + c) - (bi + di) = (a + c) - (b + d)i(a + bi) * (c + di) = ac + bci + adi + bdi * i根据定义① = (ac - bd) + (ad + bc)i 1.2.3 复数的向量与辐角 图 1 - 4向量: 既有绝对值大小又有方向的量线段的长度就是这个向量的绝对值(叫做这个向量的模)线段的方向(用箭头表示)就是这个向量的方向。求绝对值 |a| = (a * - a)^ 1/2a 与 -a 是数轴x上对称的两点而复数对称的两点分别为 a + bi 与 a - bi则 |a + bi| = [(a + bi)(a - bi)] ^ 1/2|a + bi| = ( a ^ 2 + b ^ 2) ^ 1/2 根据定义①这个向量与x轴构成的夹角就是复数辐角# tan(b/a) 1.2.4 复数的旋转
图 1 - 4向量: 既有绝对值大小又有方向的量线段的长度就是这个向量的绝对值(叫做这个向量的模)线段的方向(用箭头表示)就是这个向量的方向。求绝对值 |a| = (a * - a)^ 1/2a 与 -a 是数轴x上对称的两点而复数对称的两点分别为 a + bi 与 a - bi则 |a + bi| = [(a + bi)(a - bi)] ^ 1/2|a + bi| = ( a ^ 2 + b ^ 2) ^ 1/2 根据定义①这个向量与x轴构成的夹角就是复数辐角# tan(b/a) 1.2.4 复数的旋转  图 1 - 5在数轴上任何取一点 a + bi 连续与i 相乘4次 根据定义① 可得,则几个数分别为:1、 a + bi2、 -b + ai3、 -a - bi4、 b - aib - ai 乘以 i 又回到了 a + bi 实际上乘以 i 是复数 a + bi (a = 0, b = 1)的特殊情况那么一般情况的复数相乘又代表什么呢?定义以下复数(n为复数向量的模)p = n1(cosA + i * sinA)q = n2(cosB + i * sinB)则 pq = n1 * n2(cosA + i * sinA)(cosB + i * sinB) = n1 * n2[(cosAcosB - sinAsinB) + i(sinAcosB + cosAsinB)] = n1 * n2[cos(A + B) + isin(A + B)]可得复数相乘 1、积的模 = 两复数模的积 (n1 * n2 = n1 * n2) 2、积的辐角 = 两复数辐角的和 ( A + B = A + B)复数的相乘会使复数向量的模增加或减小,并且旋转改变该向量的方向而旋转后的角度为原复数辐角的和 ④根据④容易用复数求得方向
图 1 - 5在数轴上任何取一点 a + bi 连续与i 相乘4次 根据定义① 可得,则几个数分别为:1、 a + bi2、 -b + ai3、 -a - bi4、 b - aib - ai 乘以 i 又回到了 a + bi 实际上乘以 i 是复数 a + bi (a = 0, b = 1)的特殊情况那么一般情况的复数相乘又代表什么呢?定义以下复数(n为复数向量的模)p = n1(cosA + i * sinA)q = n2(cosB + i * sinB)则 pq = n1 * n2(cosA + i * sinA)(cosB + i * sinB) = n1 * n2[(cosAcosB - sinAsinB) + i(sinAcosB + cosAsinB)] = n1 * n2[cos(A + B) + isin(A + B)]可得复数相乘 1、积的模 = 两复数模的积 (n1 * n2 = n1 * n2) 2、积的辐角 = 两复数辐角的和 ( A + B = A + B)复数的相乘会使复数向量的模增加或减小,并且旋转改变该向量的方向而旋转后的角度为原复数辐角的和 ④根据④容易用复数求得方向  图 1 - 6如图(1-6) 在海航上,船原来的坐标是(3 ^ 1/2, i),经过45度的旋转后现在船的方向是多少复数相乘方向不考虑模的大小,因此辐角45度可以设复数为1 + i则 (3 ^ 1/2 + i)(1 + i) = (3 ^ 1/2 - 1) + (3 ^ 1/2 + 1)i即为此时的方向,此时的辐角为(3 ^ 1/2 + 1) / (3 ^ 1/2 - 1) = tan75 2、 四元数的定义2.1 四元数的记法
图 1 - 6如图(1-6) 在海航上,船原来的坐标是(3 ^ 1/2, i),经过45度的旋转后现在船的方向是多少复数相乘方向不考虑模的大小,因此辐角45度可以设复数为1 + i则 (3 ^ 1/2 + i)(1 + i) = (3 ^ 1/2 - 1) + (3 ^ 1/2 + 1)i即为此时的方向,此时的辐角为(3 ^ 1/2 + 1) / (3 ^ 1/2 - 1) = tan75 2、 四元数的定义2.1 四元数的记法  图 2 - 1欧拉证明了 一个旋转序列等价于单个旋转。想象一下,你有一根木棒,其中一端固定在一个地方,通过任意移动木棒,可以达到任意的角度(如图 2 - 1)因此, 3D空间中任意角位移都可以表示成绕单一轴的单一旋转。四元数的一般形式:q = w + xi + yj + zk w,x,y,z∈R四元数的简写形式:q = [cosA, sinA * n] ⑥ = [cosA, (sinA * n_x, sinA * n_y, sinA * n_z)]w == 木棒的长度 (i, j, k)相当于三维空间的坐标 2.1.2 复数与笛卡尔乘积
图 2 - 1欧拉证明了 一个旋转序列等价于单个旋转。想象一下,你有一根木棒,其中一端固定在一个地方,通过任意移动木棒,可以达到任意的角度(如图 2 - 1)因此, 3D空间中任意角位移都可以表示成绕单一轴的单一旋转。四元数的一般形式:q = w + xi + yj + zk w,x,y,z∈R四元数的简写形式:q = [cosA, sinA * n] ⑥ = [cosA, (sinA * n_x, sinA * n_y, sinA * n_z)]w == 木棒的长度 (i, j, k)相当于三维空间的坐标 2.1.2 复数与笛卡尔乘积  图 2 - 2设向量OA = A, 向量OB = B, 向量OC = C向量叉乘公式 C = A × B = |A||B|sin# #代表向量A、B之间的夹角 ④
图 2 - 2设向量OA = A, 向量OB = B, 向量OC = C向量叉乘公式 C = A × B = |A||B|sin# #代表向量A、B之间的夹角 ④  图 2 - 3如图(2 - 3) 假设i代表x轴的正方向, j代表y轴正方向, k代表z轴正方向根据定义④可得 i × j = k, j × k = i k × i = j, j × i = -k i × k = -j, i × k = -j ⑤可由右手定理判断正反符号,如计算i × j第一步 将右手的4个指头指向第一个数i第二步 将右手向j的方向转第三步 此时拇指 指向k的正方向 则i × j = k如计算j × i第一步 将右手的4个指头指向第一个数j第二步 将右手向i的方向转第三步 此时拇指 指向k的负方向(正方向的反方向) 则j × i = -k 2.1.3 负四元数与单位四元数设四元数q = [w, (x, y, z)], -q = [-w, (-x, -y, -z)]设点A(x, y, z), B(-x, -y, -z), 向量_OA = (x, y, z), 向量_OB = (-x, -y, -z)_OA = -_OB,则A,O,B三点共线,也就是说q与 -q旋转轴相同,又因为对于旋转轴,长度可以忽略不计,则对于四元数q = -q在几何上,单位四元数的定义为乘以任意四元数q,得到的结果为q。如图2-1,将这条线段绕多少度可以变回原来的样子,显然是360度整数倍数,又根据 ⑥ 可得单位四元数为q = [cos(360n), sin(360n)n] = [1, 0] = [-1, 0] 2.1.4 四元数的模||q|| = ||[w, (x, y, z)]|| = (w ^ 2 + x ^ 2 + y ^ 2 + z ^ 2) ^ 1/2= ||[w, v]|| = (w ^ 2 + ||v|| ^ 2) ^ 1/2 根据⑥,代入A和n可得:||q|| = ||[w, v]|| = (cosA ^ 2 + (sinA||n||) ^ 2) ^ 1/2n为单位向量,则:||q|| = (cosA ^ 2 + sinA ^ 2) ^ 1/2 = 1可得单位四元数的模为1 2.1.5 四元数的叉乘q = [w1, (x1, y1, z1)]p = [w2, (x2, y2, z3)]pq = (w1w2 − x1x2 − y1y2 − z1z2)+(w1x2 + w2x1 + y1z2 − y2z1)i+(w1y2 + w2y1 + z1x2 − z2x1)j+(w1z2 + w2z1 + x1y2 − x2y1)k = (w1w2 − x1x2 − y1y2 − z1z2)+ w1(x2i + y2j + z2k) + w2(x1i + y1j + z1k)+ (y1z2 - y2z1)i + (z1x2 - z2x1)j + (x1y2 - x2y1)k 设A = (x2i + y2j + z2k),B = (x1i + y1j + z1k)又根据:1、向量的点积 A ▪ B = x1x2(i * i) + y1y2(j * j) + z1z2(k * k)= x1x2 + y1y2 + z1z2 (向量的点积是标量 此处i = j = k = 1)2、 向量的叉乘 A × B = x1y1(i * i) + x1y2(i * j) + x1z2(i * k) + y1x2(j * i) + y1y2(j * j) + y1z2(j * k) + z1x2(k * j) + z1y2(k * j) + z1z2(k * k)在根据⑤ 化简可得 A × B = (y1z2 - y2z1)i + (z1x2 - z2x1)j + (x1y2 - x2y1)k 则pq = (w1w2 - A ▪ B) + (w1A + w2B + A × B)= [w1w2 - A ▪ B, w1A + w2B + A × B] ⑧ 结论:四元数乘积的模等于模的乘积 ⑨——> 两个单位四元数相乘的结果还是单位四元数假设p, q分别为单位四元数则p = [1, 0], q = [1, 0]||pq|| = ||1 + 0 + 0 + 0|| = ||1|| = 1||p|| * ||q|| = ||1|| * ||1|| = 1 2.1.7 四元数共轭和逆根据⑦可得q’ = [w, v]’= [w, v’]= [w, (-x, -y, -z)] ⑩ 四元数的逆为 q ^ -1, 定义为四元数的共轭除以他的模q ^ -1 = q’/ ||q|| 结论:(ab) ^ -1 = (b^-1)(a^-1)设 a = [w1, v1] b = [w2, v2]则 (ab)^-1 = (ab)’/ ||ab||根据⑧ (ab) = [w1w2 - v1 ▪ v2, w1v1 + w2v2 + v1 × v2]根据⑩ (ab)’ = [w1w2 - v1 ▪ v2, -(w1v1 + w2v2 + v1 × v2)]b’ = [w2, -v2]a’ = [w1, -v1]根据⑤⑧可得b’a’ = [w1w2 - v1 ▪ v2, -(w1v1 + w2v2 + v1 × v2)](b^-1)(a^-1) = b’a’/ ||b||||a||根据⑨ ||ab|| = ||b||||a||又因为 (ab)’ = b’a’则(ab) ^ -1 = (b^-1)(a^-1)成立可得 (q1q2q3...qn) ^ -1 = (qn)^-1...(q2^-1)(q1^-1)即四元数的乘积的逆等于各个四元数的逆以相反顺序相乘 ⑪ 2.1.8 四元数的旋转根据④可得 复数的相乘可以表示2D上的旋转那么四元数的相乘是否可以表示3D上的旋转呢?就如同三维上的点(x, y, z) 当z = 0时可以表示为二维上的点同理将四维上的点[w, v] 当w = 0时可以表示三维上的点设 p = [0, (ai, bj, ck)] q = [w1, (x1i, y1j, z1k)] (表示旋转轴) q^-1 = [w1, -(x1, y1, z1)]qp = [-(ax1 + by1 + cz1), (aw1 + cy1 - bz1)i, (bw1 + az1 - cx1)j, (cw1 + ay1 - bx1)k] pq^-1 = [(ax1 + bx1 + cz1), (aw1 - bz1 + cy1)i, (bw1 - cx1 + az1)j, (cw1 - bx1 + ay1)k]观察可得qp 与 pq^-1的第四维互为相反数,而在三维坐标上的点相同也就是说都是沿相同的方向转过了相同的角度。又因为他们的模相同则qp 与 pq^-1的几何意义是两个相同的旋转而qp 可以通过复数q与复数p相乘得到pq^-1可以通过复数q^-1与复数p相乘得到将向量q与q^-1平移到圆点,如图(2-4)所示
图 2 - 3如图(2 - 3) 假设i代表x轴的正方向, j代表y轴正方向, k代表z轴正方向根据定义④可得 i × j = k, j × k = i k × i = j, j × i = -k i × k = -j, i × k = -j ⑤可由右手定理判断正反符号,如计算i × j第一步 将右手的4个指头指向第一个数i第二步 将右手向j的方向转第三步 此时拇指 指向k的正方向 则i × j = k如计算j × i第一步 将右手的4个指头指向第一个数j第二步 将右手向i的方向转第三步 此时拇指 指向k的负方向(正方向的反方向) 则j × i = -k 2.1.3 负四元数与单位四元数设四元数q = [w, (x, y, z)], -q = [-w, (-x, -y, -z)]设点A(x, y, z), B(-x, -y, -z), 向量_OA = (x, y, z), 向量_OB = (-x, -y, -z)_OA = -_OB,则A,O,B三点共线,也就是说q与 -q旋转轴相同,又因为对于旋转轴,长度可以忽略不计,则对于四元数q = -q在几何上,单位四元数的定义为乘以任意四元数q,得到的结果为q。如图2-1,将这条线段绕多少度可以变回原来的样子,显然是360度整数倍数,又根据 ⑥ 可得单位四元数为q = [cos(360n), sin(360n)n] = [1, 0] = [-1, 0] 2.1.4 四元数的模||q|| = ||[w, (x, y, z)]|| = (w ^ 2 + x ^ 2 + y ^ 2 + z ^ 2) ^ 1/2= ||[w, v]|| = (w ^ 2 + ||v|| ^ 2) ^ 1/2 根据⑥,代入A和n可得:||q|| = ||[w, v]|| = (cosA ^ 2 + (sinA||n||) ^ 2) ^ 1/2n为单位向量,则:||q|| = (cosA ^ 2 + sinA ^ 2) ^ 1/2 = 1可得单位四元数的模为1 2.1.5 四元数的叉乘q = [w1, (x1, y1, z1)]p = [w2, (x2, y2, z3)]pq = (w1w2 − x1x2 − y1y2 − z1z2)+(w1x2 + w2x1 + y1z2 − y2z1)i+(w1y2 + w2y1 + z1x2 − z2x1)j+(w1z2 + w2z1 + x1y2 − x2y1)k = (w1w2 − x1x2 − y1y2 − z1z2)+ w1(x2i + y2j + z2k) + w2(x1i + y1j + z1k)+ (y1z2 - y2z1)i + (z1x2 - z2x1)j + (x1y2 - x2y1)k 设A = (x2i + y2j + z2k),B = (x1i + y1j + z1k)又根据:1、向量的点积 A ▪ B = x1x2(i * i) + y1y2(j * j) + z1z2(k * k)= x1x2 + y1y2 + z1z2 (向量的点积是标量 此处i = j = k = 1)2、 向量的叉乘 A × B = x1y1(i * i) + x1y2(i * j) + x1z2(i * k) + y1x2(j * i) + y1y2(j * j) + y1z2(j * k) + z1x2(k * j) + z1y2(k * j) + z1z2(k * k)在根据⑤ 化简可得 A × B = (y1z2 - y2z1)i + (z1x2 - z2x1)j + (x1y2 - x2y1)k 则pq = (w1w2 - A ▪ B) + (w1A + w2B + A × B)= [w1w2 - A ▪ B, w1A + w2B + A × B] ⑧ 结论:四元数乘积的模等于模的乘积 ⑨——> 两个单位四元数相乘的结果还是单位四元数假设p, q分别为单位四元数则p = [1, 0], q = [1, 0]||pq|| = ||1 + 0 + 0 + 0|| = ||1|| = 1||p|| * ||q|| = ||1|| * ||1|| = 1 2.1.7 四元数共轭和逆根据⑦可得q’ = [w, v]’= [w, v’]= [w, (-x, -y, -z)] ⑩ 四元数的逆为 q ^ -1, 定义为四元数的共轭除以他的模q ^ -1 = q’/ ||q|| 结论:(ab) ^ -1 = (b^-1)(a^-1)设 a = [w1, v1] b = [w2, v2]则 (ab)^-1 = (ab)’/ ||ab||根据⑧ (ab) = [w1w2 - v1 ▪ v2, w1v1 + w2v2 + v1 × v2]根据⑩ (ab)’ = [w1w2 - v1 ▪ v2, -(w1v1 + w2v2 + v1 × v2)]b’ = [w2, -v2]a’ = [w1, -v1]根据⑤⑧可得b’a’ = [w1w2 - v1 ▪ v2, -(w1v1 + w2v2 + v1 × v2)](b^-1)(a^-1) = b’a’/ ||b||||a||根据⑨ ||ab|| = ||b||||a||又因为 (ab)’ = b’a’则(ab) ^ -1 = (b^-1)(a^-1)成立可得 (q1q2q3...qn) ^ -1 = (qn)^-1...(q2^-1)(q1^-1)即四元数的乘积的逆等于各个四元数的逆以相反顺序相乘 ⑪ 2.1.8 四元数的旋转根据④可得 复数的相乘可以表示2D上的旋转那么四元数的相乘是否可以表示3D上的旋转呢?就如同三维上的点(x, y, z) 当z = 0时可以表示为二维上的点同理将四维上的点[w, v] 当w = 0时可以表示三维上的点设 p = [0, (ai, bj, ck)] q = [w1, (x1i, y1j, z1k)] (表示旋转轴) q^-1 = [w1, -(x1, y1, z1)]qp = [-(ax1 + by1 + cz1), (aw1 + cy1 - bz1)i, (bw1 + az1 - cx1)j, (cw1 + ay1 - bx1)k] pq^-1 = [(ax1 + bx1 + cz1), (aw1 - bz1 + cy1)i, (bw1 - cx1 + az1)j, (cw1 - bx1 + ay1)k]观察可得qp 与 pq^-1的第四维互为相反数,而在三维坐标上的点相同也就是说都是沿相同的方向转过了相同的角度。又因为他们的模相同则qp 与 pq^-1的几何意义是两个相同的旋转而qp 可以通过复数q与复数p相乘得到pq^-1可以通过复数q^-1与复数p相乘得到将向量q与q^-1平移到圆点,如图(2-4)所示  图 2 - 4第一次旋转为qp第二次旋转为(qp)q^-1设旋转的结果后为p’ 则p’ = qpq^-1 ⑫因为是旋转了两次,因此需要用四元数计算旋转的时候,角度是 (2 * #) / 2 = 2即按照目标角度的一半来计算 (2 * #)的几何意义为目标角度 3、 四元数的插值3.1 普通线性插值
图 2 - 4第一次旋转为qp第二次旋转为(qp)q^-1设旋转的结果后为p’ 则p’ = qpq^-1 ⑫因为是旋转了两次,因此需要用四元数计算旋转的时候,角度是 (2 * #) / 2 = 2即按照目标角度的一半来计算 (2 * #)的几何意义为目标角度 3、 四元数的插值3.1 普通线性插值 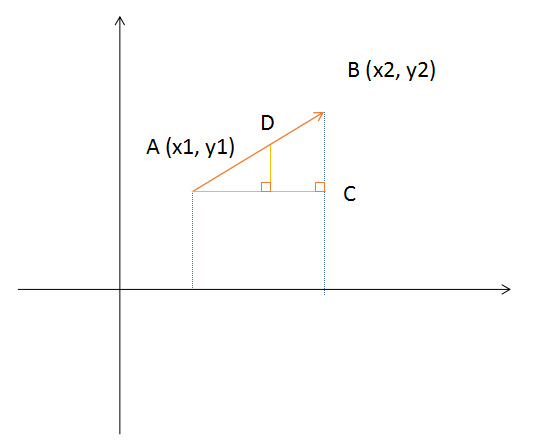 图 3 - 1如图(3-1),在一条直线AB上插入任意一个值,我们需要的是点D的坐标。如图所示过A、B点分别做x轴的垂线。分别交予x轴与点E、F。过A点做与BF的垂线,交于点C,连接AC。在AB上任意取一点D,过D点做与AC的垂线,交于点M。设D(x0, y0)则x0 - x1 = AM显然∠BAC = ∠DAMtan∠BAC = BC / ACtan∠DAM = DM / AM则 BC / AC = DM / AMAC = x2 - x1, BC = y2 - y1DM = (y2 - y1 / x2 - x1 )(x0 - x1)y0 = AE + DM = y1 + (y2 - y1 / x2 - x1 )(x0 - x1)即 y0 = y1 + (y2 - y1 / x2 - x1 )(x0 - x1)
图 3 - 1如图(3-1),在一条直线AB上插入任意一个值,我们需要的是点D的坐标。如图所示过A、B点分别做x轴的垂线。分别交予x轴与点E、F。过A点做与BF的垂线,交于点C,连接AC。在AB上任意取一点D,过D点做与AC的垂线,交于点M。设D(x0, y0)则x0 - x1 = AM显然∠BAC = ∠DAMtan∠BAC = BC / ACtan∠DAM = DM / AM则 BC / AC = DM / AMAC = x2 - x1, BC = y2 - y1DM = (y2 - y1 / x2 - x1 )(x0 - x1)y0 = AE + DM = y1 + (y2 - y1 / x2 - x1 )(x0 - x1)即 y0 = y1 + (y2 - y1 / x2 - x1 )(x0 - x1)  图 3 - 2在平面上任意取A点与B点,做向量_OA与向量_OB。连接AB,做向量_AB。在AB上任意取一点C,做向量_OC。则1. _OA + _AB = _OB, _OA + _AC = _OC因为点C在直线AB上,则_AC 与 _AB共线, 设_AC = t _AB则2. _OC = _OA + t_AB标准线性插值公式:lerp(a0, a1, t) = a0 + t△a △a = a1 - a0 ⑬设a0 = _OA, a1 = _OB 根据1与2可得_OC = a0 + t△a △a = a1 - a0 3.2 四元数插值——slerp
图 3 - 2在平面上任意取A点与B点,做向量_OA与向量_OB。连接AB,做向量_AB。在AB上任意取一点C,做向量_OC。则1. _OA + _AB = _OB, _OA + _AC = _OC因为点C在直线AB上,则_AC 与 _AB共线, 设_AC = t _AB则2. _OC = _OA + t_AB标准线性插值公式:lerp(a0, a1, t) = a0 + t△a △a = a1 - a0 ⑬设a0 = _OA, a1 = _OB 根据1与2可得_OC = a0 + t△a △a = a1 - a0 3.2 四元数插值——slerp  图 3 - 3在球形体中插值,显然轨迹是弧形的,如图(3-3)所示。显然点C在弧AB的运动过程中,线段OC的长度的不变的而普通的线性插值_OC的长度是会改变的, 如图(3-2)
图 3 - 3在球形体中插值,显然轨迹是弧形的,如图(3-3)所示。显然点C在弧AB的运动过程中,线段OC的长度的不变的而普通的线性插值_OC的长度是会改变的, 如图(3-2)  图 3 - 4sleap的基本思想是 沿4D球面上连接的两个四元数的弧插值(球面插值)把这种思想表现在平面上如图(3-4),设两个2D向量_OA与_OB,我们需要计算_OC,设w是_OA到_OB弧所截的角为了方便计算 设v0 = _OA, v1 = _OB, vt = _OC将vt表示成v0与v1的线性组合: vt = kovo + k1v1
图 3 - 4sleap的基本思想是 沿4D球面上连接的两个四元数的弧插值(球面插值)把这种思想表现在平面上如图(3-4),设两个2D向量_OA与_OB,我们需要计算_OC,设w是_OA到_OB弧所截的角为了方便计算 设v0 = _OA, v1 = _OB, vt = _OC将vt表示成v0与v1的线性组合: vt = kovo + k1v1  图 3 - 5过C点做OB的平行线,交OA与点M。分别过点B与点C做于OA的垂线,分别交线段OA于点E、M。易得△BOE与△CMF是相似三角形则 OB / BE = CM / CFOB = |v1|, BE = OB * sinw = |v1|sinwCM = k1|v1|, CF = OC*sintw = |vt|sintw = |v1|sintw (线段OC与OB长度相同,则|vt| = |v1|)代入可得: k1 = sintw / sinw ⒂
图 3 - 5过C点做OB的平行线,交OA与点M。分别过点B与点C做于OA的垂线,分别交线段OA于点E、M。易得△BOE与△CMF是相似三角形则 OB / BE = CM / CFOB = |v1|, BE = OB * sinw = |v1|sinwCM = k1|v1|, CF = OC*sintw = |vt|sintw = |v1|sintw (线段OC与OB长度相同,则|vt| = |v1|)代入可得: k1 = sintw / sinw ⒂  图 3 - 6 过C点做于OA的平行线,交OB于点E。过点E做OC的垂线,交OC于点F。易得_OE = _MC = k1v1, _EC = _OM = k0v0∠EOC = (1-t)w, ∠ECO = W线段EF = OE sin∠EOC = EC sin∠ECO则 k1|v1| sin((1-t)w) = k0|v0| sinw = k0|v1|sinw根据⒂可得: k0 = sin(1 - t)w / sinw ⒃将⒂⒃代入到 vt = kovo + k1v1可得vt = (sin(1 - t)w / sinw )vo + ( sintw / sinw)v1将同样的思想扩展到四元数,重写slerp可得:slerp(q0, q1, t) = (sin(1 - t)w / sinw )q0 + ( sintw / sinw)q1而w, 可以计算q1和q2的点积从而得出角度w:cosw = q1▪q2 / |q1||q2| 这样的作法会产生两个问题:
图 3 - 6 过C点做于OA的平行线,交OB于点E。过点E做OC的垂线,交OC于点F。易得_OE = _MC = k1v1, _EC = _OM = k0v0∠EOC = (1-t)w, ∠ECO = W线段EF = OE sin∠EOC = EC sin∠ECO则 k1|v1| sin((1-t)w) = k0|v0| sinw = k0|v1|sinw根据⒂可得: k0 = sin(1 - t)w / sinw ⒃将⒂⒃代入到 vt = kovo + k1v1可得vt = (sin(1 - t)w / sinw )vo + ( sintw / sinw)v1将同样的思想扩展到四元数,重写slerp可得:slerp(q0, q1, t) = (sin(1 - t)w / sinw )q0 + ( sintw / sinw)q1而w, 可以计算q1和q2的点积从而得出角度w:cosw = q1▪q2 / |q1||q2| 这样的作法会产生两个问题:  图 3 - 71. 可能会绕远路,将点A旋转到OB旋转轴,可以顺时针旋转也可以逆时针旋转。设∠BOA = w, 显然当w小于90度的时候,顺时针旋转所需要的路径较短,而当w大于90度的时候,逆时针旋转所需要的路径较短。首先我们需要确定w是否大于90度,可以使用:cosw = q1▪q2 / |q1||q2| 0 < w < 180因为 |q1||q2| > 0恒成立所以实际上需要计算的是q1▪q2 当q1▪q2 > 0的时候, cosw > 0 w < 90当q1▪q2 < 0的时候, cosw < 0 w > 90确定了角度之后,我们需要的是按顺时针还是逆时针旋转而四元数代表旋转轴的时候q = -q我们可以将其中一个四元数取反,总结:q1▪q2 > 0时, 旋转为q1q2q1▪q2 <= 0时, 旋转为(-q1)q2或(-q2) 2. 当w较小的时候,sinw ——> 0,sin(1 - t)w ——> 1则(sin(1 - t)w / sinw )q0 ——> ∞计算机没有真正的∞,所以我们需要确定一个sinw的范围,如当sinw < 0.0001的时候sinw = 0.0001。 4、 个人说明本文参考于《3D数学基础:图形与游戏开发》,文中内容属于个人(萌新)理解,可能会出现一些错误,欢迎大佬指正,本文仅供参考。
图 3 - 71. 可能会绕远路,将点A旋转到OB旋转轴,可以顺时针旋转也可以逆时针旋转。设∠BOA = w, 显然当w小于90度的时候,顺时针旋转所需要的路径较短,而当w大于90度的时候,逆时针旋转所需要的路径较短。首先我们需要确定w是否大于90度,可以使用:cosw = q1▪q2 / |q1||q2| 0 < w < 180因为 |q1||q2| > 0恒成立所以实际上需要计算的是q1▪q2 当q1▪q2 > 0的时候, cosw > 0 w < 90当q1▪q2 < 0的时候, cosw < 0 w > 90确定了角度之后,我们需要的是按顺时针还是逆时针旋转而四元数代表旋转轴的时候q = -q我们可以将其中一个四元数取反,总结:q1▪q2 > 0时, 旋转为q1q2q1▪q2 <= 0时, 旋转为(-q1)q2或(-q2) 2. 当w较小的时候,sinw ——> 0,sin(1 - t)w ——> 1则(sin(1 - t)w / sinw )q0 ——> ∞计算机没有真正的∞,所以我们需要确定一个sinw的范围,如当sinw < 0.0001的时候sinw = 0.0001。 4、 个人说明本文参考于《3D数学基础:图形与游戏开发》,文中内容属于个人(萌新)理解,可能会出现一些错误,欢迎大佬指正,本文仅供参考。