extend_gcd:
已知 a,b (a>=0,b>=0)
求一组解 (x,y) 使得 (x,y)满足
gcd(a,b) = ax+by
下面代码中d = gcd(a,b),顺便求出gcd
可以扩展成求等式 ax+by = c,但c必须是d的倍数才有解,即 (c%gcd(a,b))==0
注意求出的 x,y 可能为0或负数 =================================== 乘法逆元: a*b %n == 1 已知 a, n, 求b 就是乘法逆元 ===================================
中国剩余定理: 给定方程组: x%a[0] = m[0] x%a[1] = m[1] ··· x%a[n-1] = m[n-1] 求变量x 的值 m必须互质 当m不互质时用合并方程的做法: (合并方程的原因:当我们把n条方程合并成1条时就是extend能求的了,extend能求一条方程的解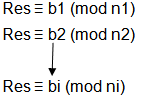
问题描述:给出bi,ni的值,且n1, n2, n3,…, ni两两之间不一定互质,求Res的值?
解:采用的是合并方程的做法。
这里将以合并第一第二个方程为例进行说明
由上图前2个方程得(设k1、k2为某一整数):
所以我们简化一下结论: 已知方程组(b1,b2,n1,n2是已知量): res%b1 = n1 res%b2 = n2 -> 合并两条方程得到: res % ( (n1*n2)/d ) = b1+n1*( K%(n2/d)) 其中K = (k1*(b2-b1)/d) % (n2/d);
其中d = gcd(n1,n2); 其中k1: k1*n1 - k2*n2 = b2-b1 k1,d 可以直接由extend_gcd得到 extend_gcd(n1,n2,d,k1,k2); (b2-b1)%d == 0 说明extend跑出的k1是一个解,否则说明不存在满足解的k1 注意求K时:为了得到最小非负整数K,所以用一个取模的技巧 K = (K%mod+mod)%mod; 例题及题解:点击打开链接 ================================== 若 a == b (mod n) 能推出下面2条等式 1: (a+c) == b+c (mod n) 2:ac == bc (mod n) (但 ac==bc(mod n) 不能推出 a==b(mod n))
注意求出的 x,y 可能为0或负数 =================================== 乘法逆元: a*b %n == 1 已知 a, n, 求b 就是乘法逆元 ===================================
中国剩余定理: 给定方程组: x%a[0] = m[0] x%a[1] = m[1] ··· x%a[n-1] = m[n-1] 求变量x 的值 m必须互质 当m不互质时用合并方程的做法: (合并方程的原因:当我们把n条方程合并成1条时就是extend能求的了,extend能求一条方程的解
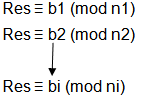
问题描述:给出bi,ni的值,且n1, n2, n3,…, ni两两之间不一定互质,求Res的值?
解:采用的是合并方程的做法。
这里将以合并第一第二个方程为例进行说明
由上图前2个方程得(设k1、k2为某一整数):

所以我们简化一下结论: 已知方程组(b1,b2,n1,n2是已知量): res%b1 = n1 res%b2 = n2 -> 合并两条方程得到: res % ( (n1*n2)/d ) = b1+n1*( K%(n2/d)) 其中K = (k1*(b2-b1)/d) % (n2/d);
其中d = gcd(n1,n2); 其中k1: k1*n1 - k2*n2 = b2-b1 k1,d 可以直接由extend_gcd得到 extend_gcd(n1,n2,d,k1,k2); (b2-b1)%d == 0 说明extend跑出的k1是一个解,否则说明不存在满足解的k1 注意求K时:为了得到最小非负整数K,所以用一个取模的技巧 K = (K%mod+mod)%mod; 例题及题解:点击打开链接 ================================== 若 a == b (mod n) 能推出下面2条等式 1: (a+c) == b+c (mod n) 2:ac == bc (mod n) (但 ac==bc(mod n) 不能推出 a==b(mod n))
#include
#include
#include
#include
#include
#include
#include
#include
#include