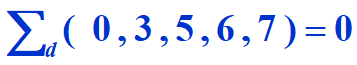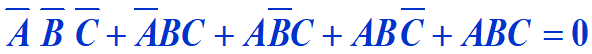class="markdown_views prism-tomorrow-night">
数字化时代
随着微电子技术的发展,‘0’/'1’二进制不再只与计算机相关,而是应用与数码相机 / MP4 / 数字电视 / 数控机床 / 数字通信 等领域
数字化的优点
数据压缩data compression + 纠正错误error correction
模拟信号


逻辑变量取值
0 and 1
逻辑基本运算
"与"运算
Y = A * B = A B
真值表
 "与门"逻辑符号
"与门"逻辑符号

"或"运算
Y= A + B
真值表
 "或门"逻辑符号
"或门"逻辑符号

"非"逻辑

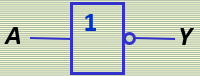
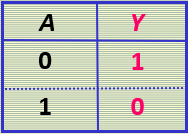 "非门"逻辑符号
"非门"逻辑符号
三种常用复合逻辑
图示
"与非"逻辑
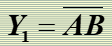
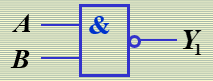 "或非"逻辑
"或非"逻辑
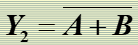
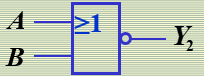 "与或非"逻辑
"与或非"逻辑
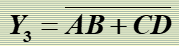
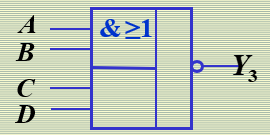 "异或"逻辑
"异或"逻辑
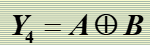
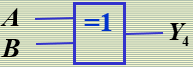
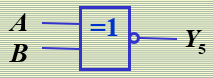
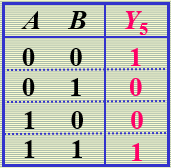
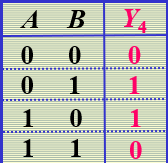 "异或非"逻辑
"异或非"逻辑
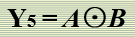
德摩根定律
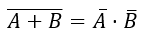
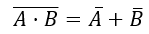

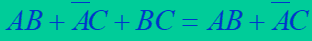
求逻辑函数的反函数
步骤1 : A变量与非A变量 互换
步骤2 : " 乘 " 与 " + " 互换
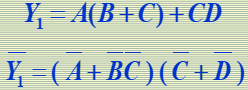
最小项:

 3个变量有222=8个最小项
3个变量有222=8个最小项
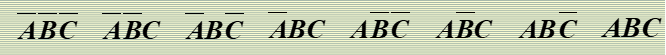 最小项编号
最小项编号

"与或"式 = 只由"于式"和"或式"组成
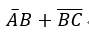
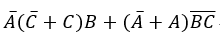 “最简与或式”
"标准与或式"的基础上进行的化简
"最简与或式"的结构
“最简与或式”
"标准与或式"的基础上进行的化简
"最简与或式"的结构
 标准式写法
标准式写法
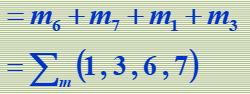
函数的公式化化简
形式
并项法
 吸收法
吸收法
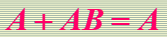 消去法
消去法
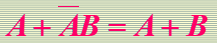 配项消项法
配项消项法

二个变量的卡诺图

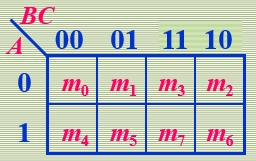 四个变量的卡诺图
四个变量的卡诺图
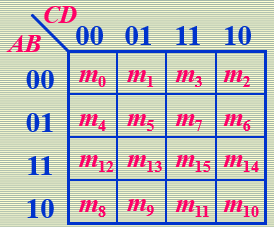 五变量的卡诺图
五变量的卡诺图
 六个变量的卡诺图
无法使用图形法进行化简
卡诺图的特点:
上下相邻与左右相邻都是逻辑相邻 / 单列与单行的头尾也是逻辑相邻 / 对折起来重合的位置也是逻辑相邻
逻辑相邻:
逻辑相邻的两个最小项目意味着只有一个变量是存在自身与它的反变量,其他变量都是相同的,所以可以消去该变量
相邻与相对的合并
六个变量的卡诺图
无法使用图形法进行化简
卡诺图的特点:
上下相邻与左右相邻都是逻辑相邻 / 单列与单行的头尾也是逻辑相邻 / 对折起来重合的位置也是逻辑相邻
逻辑相邻:
逻辑相邻的两个最小项目意味着只有一个变量是存在自身与它的反变量,其他变量都是相同的,所以可以消去该变量
相邻与相对的合并
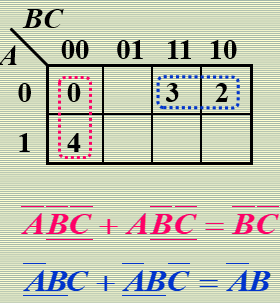
 四个相邻或四个相对4个变量可以消去2个变量
四个相邻或四个相对4个变量可以消去2个变量
 八个相邻一共四个变量可以消去三个三个变量
八个相邻一共四个变量可以消去三个三个变量
 总结:
总结:
 技巧:如何快速用消解因子
1:先读图(找相邻/相对的可以消解的方块) ==> 2:将每个方块编号竖着排列在草稿本 => 3:对比编号,保留相同的位置 ==> 再转化为最后的变量结果
技巧:如何快速用消解因子
1:先读图(找相邻/相对的可以消解的方块) ==> 2:将每个方块编号竖着排列在草稿本 => 3:对比编号,保留相同的位置 ==> 再转化为最后的变量结果
举例
A=1表示升 / B=1表示降 / C=1表示停
约束=不可能取的值
000 / 011 / 101 / 110 / 111
约束项=约束的字母写法
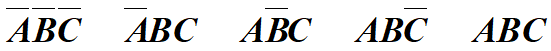 约束条件=所有约束项之和仍为0
约束条件=所有约束项之和仍为0
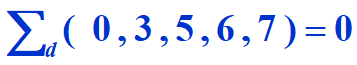
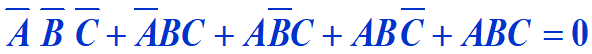
逻辑"最简与或式"函数与真值表与逻辑电路图之间的相互转化
- 处理模拟信号的电路 = 模拟电路(主要解决信号的失真问题)
- 处理数字信号的电路 = 数字电路(主要考虑信号的传输,存储,计数等问题)
- 与运算=并且=同时满足
- 卡诺图:体现逻辑相邻的方格图
- 最小项下标号的由来:任意一个最小项只有一个赋值能使该项成立,例:ABC有8种取值方式,但是只有( 1 , 1 , 1 ) 能使ABC == 1,所以 ABC ==m7 .
- 注意:与或式,"与式"与"或式"不能有嵌套的关系,但是可以嵌套"非式"的关系
- 为什么要对"标准与或式"化简为"最简与或式" 答:因为能大量简化硬件的门电路结构,达到相同的效果
数字化时代


逻辑代数的基本概念,公式,定理
 "与门"逻辑符号
"与门"逻辑符号

 "或门"逻辑符号
"或门"逻辑符号


 "非门"逻辑符号
"非门"逻辑符号

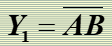
 "或非"逻辑
"或非"逻辑
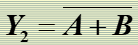
 "与或非"逻辑
"与或非"逻辑
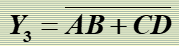
 "异或"逻辑
"异或"逻辑
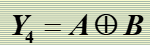

 "异或非"逻辑
"异或非"逻辑
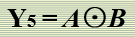


/**公式**/
与: 0*0=0 或: 1+1=1(注意)
0*1=0 1+0=1
1*1=1 0+0=0
A*1=A A+0=A
A*0=0 A+1=1(注意)
定理: A*B=B*A A+B=B+A
A*A=A A+A=A
(A*B)*C=A*B*C (A+B)+C=A+B+C
A(B+C)=AB+AC A+BC=(A+B)(A+C) //(注意)
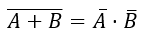
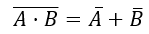

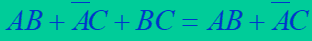
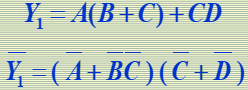
逻辑函数的公式化简与图像化简

 3个变量有222=8个最小项
3个变量有222=8个最小项
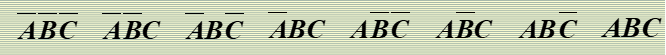 最小项编号
最小项编号

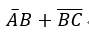
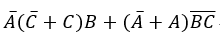 “最简与或式”
"标准与或式"的基础上进行的化简
"最简与或式"的结构
“最简与或式”
"标准与或式"的基础上进行的化简
"最简与或式"的结构
 标准式写法
标准式写法
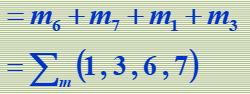
 吸收法
吸收法
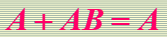 消去法
消去法
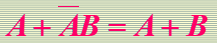 配项消项法
配项消项法

逻辑函数的图像化简法

 四个变量的卡诺图
四个变量的卡诺图
 五变量的卡诺图
五变量的卡诺图
 六个变量的卡诺图
无法使用图形法进行化简
卡诺图的特点:
上下相邻与左右相邻都是逻辑相邻 / 单列与单行的头尾也是逻辑相邻 / 对折起来重合的位置也是逻辑相邻
逻辑相邻:
逻辑相邻的两个最小项目意味着只有一个变量是存在自身与它的反变量,其他变量都是相同的,所以可以消去该变量
相邻与相对的合并
六个变量的卡诺图
无法使用图形法进行化简
卡诺图的特点:
上下相邻与左右相邻都是逻辑相邻 / 单列与单行的头尾也是逻辑相邻 / 对折起来重合的位置也是逻辑相邻
逻辑相邻:
逻辑相邻的两个最小项目意味着只有一个变量是存在自身与它的反变量,其他变量都是相同的,所以可以消去该变量
相邻与相对的合并

 四个相邻或四个相对4个变量可以消去2个变量
四个相邻或四个相对4个变量可以消去2个变量
 八个相邻一共四个变量可以消去三个三个变量
八个相邻一共四个变量可以消去三个三个变量
 总结:
总结:
 技巧:如何快速用消解因子
1:先读图(找相邻/相对的可以消解的方块) ==> 2:将每个方块编号竖着排列在草稿本 => 3:对比编号,保留相同的位置 ==> 再转化为最后的变量结果
技巧:如何快速用消解因子
1:先读图(找相邻/相对的可以消解的方块) ==> 2:将每个方块编号竖着排列在草稿本 => 3:对比编号,保留相同的位置 ==> 再转化为最后的变量结果
具有约束的逻辑函数的化简
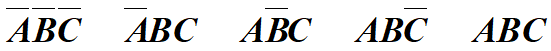 约束条件=所有约束项之和仍为0
约束条件=所有约束项之和仍为0