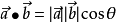基础：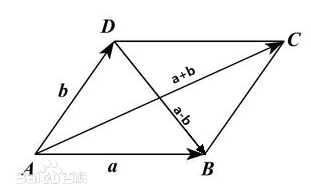
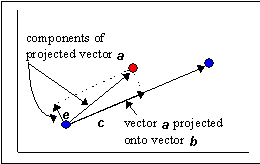
点乘法：向量c为向量a在向量b上的投影向量，求得向量e的模即可求得最终结果。向量a已知，并且e=a-c，则问题转化为求向量c。向量c的方向很容易确定，即b.normalized；而向量c的模|c|=|a|·cosθ，则求出cosθ即可。由向量的点乘很容易知道a·b = |a||b|cosθ，则最终问题得以解决。叉乘法：|axb|等于它们所张开的平行四边形的面积S。S除以|b|即等于点到直线的距离。
- 单位向量：模等于1的向量，一个非零向量除以它的模，可得所需单位向量。
- 向量的加减法：
- 向量的投影：设两个非零向量a与b的夹角为θ，则将|b|·cosθ 叫做向量b在向量a方向上的投影
- 向量的点乘：
- 向量的叉乘：
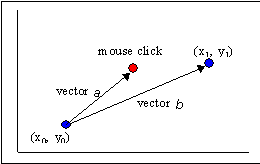
模长：示例：红 {MOD}的点为鼠标位置，蓝 {MOD}的点(x0,y0)，(x1,y1)为直线上的两个点，求红 {MOD}的点到直线的距离，即长度在数值上等于以向量a、b、夹角θ组成的平行四边形的面积。方向：与这两个向量所在的平面垂直，且遵守右手定则（或左手定则）。
将问题进行一下转化：如下图所示
{var%20f='http://v.t.sina.com.cn/share/share.php?appkey=1515056452',u=z||d.location,p=['&url=',e(u),'&title=',e(t||d.title),'&source=',e(r),'&sourceUrl=',e(l),'&content=',c||'gb2312','&pic=',e(p||'')].join('');function%20a(){if(!window.open([f,p].join(''),'mb',['toolbar=0,status=0,resizable=1,width=440,height=430,left=',(s.width-440)/2,',top=',(s.height-430)/2].join('')))u.href=[f,p].join('');};if(/Firefox/.test(navigator.userAgent))setTimeout(a,0);else%20a();})(screen,document,encodeURIComponent,'','','https://www.xiaopingtou.cn//data/attach/topic/topicKPo7gB.jpg', '推荐 lwlwl 的文章《使用向量的方法计算点到直线的距离》','https://www.xiaopingtou.net/article-57145.html','页面编码gb2312|utf-8默认gb2312'));){kind=link}
点乘法：向量c为向量a在向量b上的投影向量，求得向量e的模即可求得最终结果。向量a已知，并且e=a-c，则问题转化为求向量c。向量c的方向很容易确定，即b.normalized；而向量c的模|c|=|a|·cosθ，则求出cosθ即可。由向量的点乘很容易知道a·b = |a||b|cosθ，则最终问题得以解决。叉乘法：|axb|等于它们所张开的平行四边形的面积S。S除以|b|即等于点到直线的距离。