有限域和离散对数问题

这篇文章是ECC系列的第二篇 在上一篇文章中，我们看到了基于实数域的的椭圆曲线如何构成了群（Group），我们如下定义了群中的加法：P + Q + R = 0，我们分别用几何方法和代数方法计算了了椭圆曲线点的加法。
随后，我们有介绍了数乘（nP = P + P + P + … + P），然后找到了一个较为快速的计算nP的算法：double and add。 现在，我们要限制我们的椭圆曲线在有限域上（实数域不是有限域），而不是实数域，让我们来看看有哪些变化。 The field of integers modulo p 有限域，首先是一个拥有有限元素的几何。例如，一个简单的有限域就是以素数p为模数的数的集合（模P余数的集合，即模p剩余类环），常被写为Z/p，GF(P)，Fp，我们在后文会这么描述一个模P的有限域。 在域中，我们有2种二元运算，加法 和 乘法，两者运算都是封闭的、满足结合律、分配率。两个运算都是唯一的单位元。并且对于每一个元素，都有唯一的逆元。最后，乘法对加法满足分配率：x *( y + z) = x*y + x*z. 整数模p的集合，包括了从0~p-1的数，加法和乘法的运算都是模p的。下面是F23例子。 加法:(18 + 9)mod 23 = 4
减法:(7 - 14) mod 23 = 16
乘法:4 * 7 mod 23 = 5
加法逆元: x + 5 = 0 mod 23 => x= 18
乘法逆元: x *9 = 1 mod 23 => x= 18
（上面两个例子和原文中不一样，个人觉得原文中举例不恰当。
作为加法群，单位元为0，作为乘法群，单位元为1。
乘法逆元使用欧几里得拓展算法可求x，即 9x - 23y = 1，辗转相除即可求得x值x = -5，去其最小正整数则为18。
） 上文已说过，如果p是素数，则模p剩余类环是域。P是素数很重要，如果p不是素数，比如p=4，则集合Zp={0, 1, 2, 3}，显然2没有逆元。
(
2*1 mod 4 = 2
2*2 mod 4 = 0
2*3 mod 4 = 2
没有逆元
) 模p作用的除法运算 我们将要定义在Fp上的椭圆曲线，但是在这之前，我们需要弄清几点概念。
x/y代表什么？数论中，x/y表示 x* y^-1，即 x 乘上 y的逆元。所以除法运算分为两步：第一步求逆元，第二步计算乘法。
乘法逆元可以使用欧几里得拓展算法轻松的计算，这里不多讲欧几里得拓展算法的细节，只是贴出Python代码 def extended_euclidean_algorithm(a, b):
“””
Returns a three-tuple (gcd, x, y) such that
a * x + b * y == gcd, where gcd is the greatest
common divisor of a and b. This function implements the extended Euclidean algorithm and runs in O(log b) in the worst case. """ s, old_s = 0, 1 t, old_t = 1, 0 r, old_r = b, a while r != 0: quotient = old_r // r old_r, r = r, old_r - quotient * r old_s, s = s, old_s - quotient * s old_t, t = t, old_t - quotient * t return old_r, old_s, old_t def inverse_of(n, p):
“””
Returns the multiplicative inverse of
n modulo p. This function returns an integer m such that (n * m) % p == 1. """ gcd, x, y = extended_euclidean_algorithm(n, p) assert (n * x + p * y) % p == gcd if gcd != 1: # Either n is 0, or p is not a prime number. raise ValueError( '{} has no multiplicative inverse ' 'modulo {}'.format(n, p)) else: return x % p Fp上的椭圆曲线 现在，我们可以在Fp上来定义椭圆曲线，上篇文章中，椭圆曲线如下描述：
而现在变成了下面的描述：
当然，0依旧表示无限远的点，也即单位元；参数a、b在Fp上
上面四张图，分别是 曲线方程 Y^2≡x^3−7x+10(modp) 参数p取为19,97,127,487的几何图形。（显然，p越小，集合Fp中的元素越少，满足Fp的椭圆曲线的点也越少）
当然，我们也可以证明，在Fp上的椭圆曲线的点，构成阿贝尔群（交换群）。 点加 在实数域，我们定义了三个“aligned”的点相加结果为0，P + Q+ R = 0，当然，该定义在Fp上也适用。实数域上“aligned”就是共线，但是Fp上，我们需要重新定义“aligned”。 Fp上，如果(x, y)满足方程(ax + by+ c ) mod p = 0，则这些(x, y)是共线的. 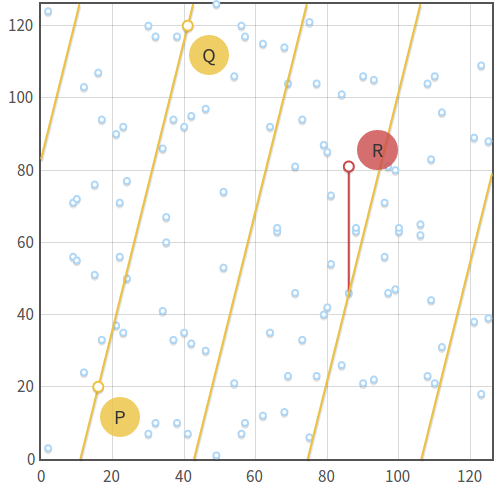上图中，是椭圆曲线方程y^2 = X^3 - x + 3 mod 127 的所有点。
点P(16,20), Q(41, 120)，则方程y = 4x + 83(mod 127) 和 椭圆曲线方程相交于点P。 当然，点的加法依旧保持了原有的性质：
(1):Q + 0 = 0 + Q = Q
(2):Q及其逆元-Q，实数域上他两关于X轴对称，但是在Fp上，-Q = (Xq, -Yq mod p)
(3):p + (-P) = 0 代数方法计算加法
计算点的等式和上篇文章中基本差不多，唯一的区别就是在等式中加上mod p.

其中，如果P不等于Q，则

如果P等于Q则
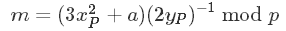和在实数域的椭圆曲线点加法差不多吧，这可不是巧合。这个等式可以用于任何的域，除了F2、F3不适用。 几何方法计算加法 我们不会定义几何方法，实际上，这样的话我们会碰到一些问题。比如，上篇文章中，我们说了要计算p + p，我们需要获得点p和椭圆曲线的切线，但是由于点非连续，切线就没有意义了。 椭圆曲线的阶
我们说过，椭圆曲线定义在有限域上，这也意味着，椭圆曲线上的点也是有限的。所以我们引出了一个问题：一个椭圆曲线到底有多少个点。 首先我们定义“椭圆曲线上点的个数”为 椭圆曲线的 阶 (order)。 当然，把x暴力的从0遍历到 p-1 肯定不是一个好方法，意味它需要p个步骤，如果p很大，那就非常慢。 幸运的是，有一个快速的方法计算椭圆曲线的阶。
https://en.wikipedia.org/wiki/Schoof%27s_algorithm 数乘和循环子群 在实数域中，乘法可以被定义成这样：
我们可以使用 dobule and add 算法来计算乘法，算法复杂度是O(logn)。
但是椭圆曲线上的乘法有一个非常有趣的性质。
假设 Y^2 = X^3 + 2x + 3 mod 97 和 其上的点P (3, 6)，我们来计算一下nP：
nP的取值只有5个不一样的点(0, P, 2P, 3P, 4P)，然后他们周期循环。明显的，椭圆曲线上的数乘和模运算类似： 0P = 0
1P = (3,6)
2P = (80, 10)
3P = (80, 87)
4P = (3, 91)
5P = 0
6P = (3, 6)
7P = (80, 10)
8P = (80, 87)
9P = (3, 91) 我们需要指出两件事，点P的倍数的结果只有出现5个点，其他的点从未出现；其次他们是周期出现的，所以我们可以这样描述： 对于任意的K，如下等式成立
5kP = 0
(5k + 1)P = P
(5k + 2)P = 2P
(5k + 3)P = 3P
(5k + 4)P = 4P 当然，上面的多个等式可以写成一个等式
kP = (K mod 5) P 显然，上面的5个点的集合，运算是封闭的。
当然，不仅仅P有这样的性质，其他点也有类似的性质。
即，P的加法构成了一个群S，由于S属于G，故S是G的子群。
循环子群是ECC的基础。 子群的阶 我们可以问自己，由P生成的子群的阶是什么？ 1：首先，我们已经定义了阶就是群中点的个数。在子群中也是这样的，但是我们可以换一种表达方式：子群的阶是最小能够使得nP=0的n。就像上文中给出的例子，n是5。
2：子群的阶和群的阶是有关系的。拉格朗日定理说明了，子群的阶是群的阶的因子。即如果N是群的阶，则其子群的阶n，则n|N。 上述向我们给出了一个找到子群的阶的方法
（1）计算群的阶N
（2）找出所有N的因子
（3）每个N的因子n，然后乘以P
（4）在3中，找出最小的n，使得满足nP = 0。则这个n是子群的阶。 例如，假设在F37上定义椭圆曲线 y^2 = X^3 - x + 3，显然群的阶可以轻松算出为N = 42，子群的阶是n 可能是 1,2,3,6,7,14,21,42。
设曲线上的点P(2, 3)，由于P 不等于0、2P不等于0……7P等于0，故P的阶是7。即由P生成的子群的阶是7。 注意，“最小的n”是非常重要的。如果随机的遍历0 ~ 42，则很有可能遍历到14,14P也是0，但是14不是P的阶。 另外一个例子，在F29上定义一个椭圆曲线：y^2 = x^3 - x + 1 ，则椭圆曲线的阶为N=37，由于37是素数，所以其因子只有1和37。如果子群的阶为1，则显然，该子群包含一个点，该点就是0.如果子群的阶是37，则该子群就是parent群。 找一个基点 在ECC算法种，我们希望找到一个阶数较大的子群。
通常我们会选择一个椭圆曲线，然后计算它的阶N，选择一个较大的因子n，然后找一个合适的基点。也就是说，我们不是首先找一个基点，然后计算它的阶，而是相反，我们先找到一个合适的阶，然后找以这个数为阶的子群的生成元。
怎么找呢？
首先，拉格朗日揭示，h = N/n是一个整数（当然，n是N的因子），h有一个自己的名字：cofactor of the subgroup。 首先，每个椭圆曲线上的点P，NP = 0，因为N是P的阶n的倍数。
我们可以写成这样 n(hP) = 0。
假设n是一个素数（下篇文章会讲到为什么），我们令G= hP，则G就是子群的生成元。 我们总结一下：
1：计算椭圆曲线的阶N。
2：选择一个数n当成子群的阶。n应该是N的素因数
3：计算h = N/n
4：随机选择一个点P
5：计算G = hP
6：如果G是0，到第4步。否则，我们找到了这个基点。 n必须是素数，若非如此，则nP = 0不一定表示n是P的阶，因为P的阶可能是n的一个因子。 离散对数 接下来我们需要考虑一个问题
如果我们知道了P和Q，Q是P的倍数，我们计算这个倍数k？ 这个问题就是基于椭圆曲线的离散对数问题，他被认为是很难解的问题。
目前为止没有找到在多项式时间(Polynomial time)内能够解决这个的方法，同样的，这个难题也没有数学上的严格证明。 这个难题也和其他密码学中的离散对数问题类似，例如DSA算法，DH密钥交换算法，ElGamal 算法，他们名字基本类似不是没有原因的，因为都是基于离散对数问题。只是上述例子中，使用了模幂运算，而不是我们椭圆曲线的数乘运算。
模幂运算的离散对数问题可以这么描述：
我们知道a 和 b是有这么一个等式关系 b = a^k mod p，给你一个a,b,p，让你求k。当然不管是模幂运算的DH还是椭圆曲线数乘的DH，他们的值都是离散的。因为值都取自于有限集合（子群），称之为对数，因为你要计算这个难题，需要对数运算。 ECC有趣的地方就是，它的离散对数问题，看起来比其他的离散对数问题难多了，这也意味着，在椭圆曲线算法中，我们可以使用更小的值k，来达到其他离散对数难题中同样的安全效果。