• 第二章答案

第二章答案

1. 异众比率(variation ratio)：用Vr表示，其定义为：Vr=∑fi−fm∑fi=1−fm∑fi，其中∑fi表示变量值的总频数，∑fm表示众数组的频数。异众比率主要用于衡量众数对一组数据的代表程度。异众比越大，说明非众数组的频数占总频数的比重越大，众数的代表性就越差；异众比越小，说明非众数组的频数占总频数的比重越小，众数的代表性就越好。异众比率主要适合测度分类数据的离散程度，当然，对于顺序数据与数值数据也可以进行计算。
2. 标准分数（standard score）:变量值与其平均数的差除以标准差后的值。设标准分数为z，则有z=xi−x¯s标准分数给出了一组数据中各数值的相对位置。实际上，z分数只是将原始数据进行了线性变换，它并没有改变一个数据在该组数据中的位置，也没有改变该组数据的分布形状。
3. 相对离散程度：离散系数（coefficient of variation）：一组数据的标准差与其相应的平均数之比称为离散系数，也称变异系数。为了消除变量值水平高低（即两个相同类型的属性其值的分布差别特别大，比如一个为几百万，而另一个为几万或几十万）和计量单位不同对离散程度测度值的影响，需要计算离散系数，其计算公式为：vx=sx¯离散系数的作用主要是用于比较不同样本的离散程度。离散系数越大，说明离散程度越大。离散系数越小，说明离散程度就越小（当平均数趋于零时，离散系数就趋于无穷大，此时需要按照实际情况进行解释）。

1. 该数的均值是多少？中位数是什么？
   该数的均值为29.963，中位数是25。
2. 该数据的众数是什么？讨论数据的模态（即二模、三模等）。
   该数据的众数为25和35，即该数据是一个双峰的分布，即二模。
3. 该数据的中列数是多少？
   该数据的中列数为(70+13)/2=41.5。
4. 你能粗略的找出该数据的第一个四分位数(Q1)和第三个四分位数(Q3)吗？
   第一个四分位数为：⌈274⌉=7处，Q1=20，第三个四分位数为：7∗3=21处，Q3=35。
5. 给出该数据的五数概括。
   根据以上，得到了最小观测值、Q1、Q2、Q3、最大观测值，所以画出其盒图如下：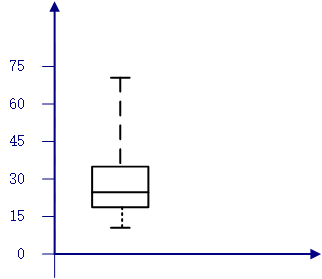
6. 分位数-分位数图与分位数图有什么区别？
   分位数图(quantile plot)是一种观察单变量数据分布的简单有效方法。首先它显示给定属性的所有数据的分布情况；其次，它绘出了分位数信息（即对于某序数或数值属性X，设xi(i=1,...,N)是按照递增排序的数据，使得x1是最小的观测值，xN是最大的观测值）。
   分位数-分位数图(q-q图)则是反映了同一 个属性的不同样本的数据分布情况，使得用户可以很方便的比较这两个样本之间的区别或者联系。

1. 解题思路：由于该题目并没有说明某一个年龄对应的人数有多少个，所以一种解题思路就是取每一个年龄区间的中位数乘以其人数，然后再除以总的人数从而计算所有数据的中位数。median=3×200+10×450+18×300+35×1500+65×700+95×44200+450+300+1500+700+44≃35

1. 标称属性
   标称属性的相异性可以根据不匹配率去计算：d(i,j)=p−mp其中，p为刻画对象的属性总数，m是匹配的数目（即i和j取值相同状态的属性数）
2. 非对称的二元属性
   非对称的二元相异性可以依据二元属性的列联表去计算，计算公式如下：
   d(i,j)=r+sq+r+s具体标号含义详解课本第71页。
3. 数值属性
   数值属性可以有闽可夫斯基距离(Minkowski distance)，它是欧几里得距离和曼哈顿距离的推广，定义如下：
   d(i,