{var%20f='http://v.t.sina.com.cn/share/share.php?appkey=1515056452',u=z||d.location,p=['&url=',e(u),'&title=',e(t||d.title),'&source=',e(r),'&sourceUrl=',e(l),'&content=',c||'gb2312','&pic=',e(p||'')].join('');function%20a(){if(!window.open([f,p].join(''),'mb',['toolbar=0,status=0,resizable=1,width=440,height=430,left=',(s.width-440)/2,',top=',(s.height-430)/2].join('')))u.href=[f,p].join('');};if(/Firefox/.test(navigator.userAgent))setTimeout(a,0);else%20a();})(screen,document,encodeURIComponent,'','','https://www.xiaopingtou.cn//data/attach/topic/topicKPo7gB.jpg', '推荐 粽子啊 的文章《Codeforces 801C Voltage Keepsake》','https://www.xiaopingtou.net/article-57400.html','页面编码gb2312|utf-8默认gb2312'));){kind=link}
原题传送
题意：n个设备同时使用，第i个设备每秒消耗ai个单位的电，开始时有bi个单位的电。有一个充电器，每秒充p个单位的电，每次只能充一个设备，充电时间可以为任意的实数，且假设不需要时间更换充电设备。问这n个设备中直到存在一个电量为0个单位的设备时最多能用多长时间。如果能用无限长的时间，输出-1。
一开始先把所有设备的a加起来，即a1+a2+……+an，把算出的结果与p比较，若p>= a1+a2+……+an，则能用无限长的时间，输出-1。 如果不能用无限长的时间，我们假设充电器充到了一个充电宝里，这个充电宝能充无限的电量，充电宝能充无限个设备，而当前充电宝的电量为pow。把所有设备在不充电时能用的时间算出来(这里假设第i个设备能用ti秒)再进行升序排序，然后让时间短的设备先充电，让这些设备能用更长的时间。这里设需要充电的设备为1~m，sum=a1+a2+……+am ，充电后让时间延长至tm+1（前提是有足够的电量维持，此时pow+(tm+1 -tm )*p >= (tm+1 -tm)*sum），如果不能让时间延长至tm+1,算出他们最多能延长到的时间（设为tmax），这个时间就是答案。 还有一种情况，就是电量足以延长至tn，此时就延长所有设备的使用时间至最大值，这个时间就是答案。关键是怎么求tmax呢？令x = tmax-tm, 则tmax= tm+x，故：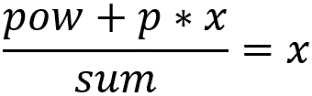
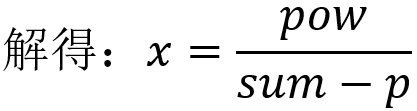
下面用数据来解释一下吧： 第一组数据： 2 1 2 2 2 1000 首先求：a1+a2+……+an=4，而p=1<4=a1+a2+……+an，因此不能用无限长的时间。 把所有设备在不充电时能用的时间算出来： 第一个设备能用2/2=1s，t1=1s, a1=2 第二个设备能用1000/2=500s，t2=500s, a2=2 排序后： t1=1s, a1=2 t2=500s, a2=2 此时充电宝电力为pow=t1*p=1 先充第1个设备(m=1)，此时sum=a1=2，由于pow + (t2 -t1) * p < (t2 -t1)*sum，所以不能让时间延长至t2，x=pow/(sum-p)=1/1=1s，故tmax= tm+x=1+1=2s 所以答案为：2
再看第二组数据： 1 100 1 1 首先求：a1+a2+……+an=1，而p=100>1=a1+a2+……+an，因此能用无限长的时间。输出-1 。
再看第三组数据： 3 5 4 3 5 2 6 1 首先求：a1+a2+……+an=15，而p=5<15=a1+a2+……+an，因此不能用无限长的时间。
把所有设备在不充电时能用的时间算出来： 第一个设备能用3/4=0.75s，t1=0.75s, a1=4 第二个设备能用2/5=0.4s，t2=0.4s, a2=5
第三个设备能用6/1=0.166666666666667s，t3=0.166666666666667s, a3=6
排序后： t1=0.166666666666667s, a1=6
t2=0.4s, a2=5
t3=0.75s, a3=4
此时充电宝电力为pow=t1*p=0.833333333333333 先充第1个设备(m=1)，此时sum=a1=6，由于pow + (t2 -t1) * p > (t2 -t1)*sum ，所以能让时间延长至t2 此时pow=pow（原来的电量）+(tm+1 -tm)*p（这段时间充的电量）- (tm+1 -tm)*sum（让设备1用的时间延长至t2所耗的电量） =pow+ (tm+1 -tm)*(sum-p) 故pow=0.833333333333333+（0.4-0.166666666666667）*（5-6）= 0.6 接着充1-2两个设备(m=2)，此时sum=a1+a2=11，由于pow + (t3 -t2) * p < (t3 -t2)*sum，所以不能让时间延长至t3 此时x=pow/(sum-p)=0.6/6=0.1s 故tmax= t2+x=0.4+0.1=0.5s
附上代码：
一开始先把所有设备的a加起来，即a1+a2+……+an，把算出的结果与p比较，若p>= a1+a2+……+an，则能用无限长的时间，输出-1。 如果不能用无限长的时间，我们假设充电器充到了一个充电宝里，这个充电宝能充无限的电量，充电宝能充无限个设备，而当前充电宝的电量为pow。把所有设备在不充电时能用的时间算出来(这里假设第i个设备能用ti秒)再进行升序排序，然后让时间短的设备先充电，让这些设备能用更长的时间。这里设需要充电的设备为1~m，sum=a1+a2+……+am ，充电后让时间延长至tm+1（前提是有足够的电量维持，此时pow+(tm+1 -tm )*p >= (tm+1 -tm)*sum），如果不能让时间延长至tm+1,算出他们最多能延长到的时间（设为tmax），这个时间就是答案。 还有一种情况，就是电量足以延长至tn，此时就延长所有设备的使用时间至最大值，这个时间就是答案。关键是怎么求tmax呢？令x = tmax-tm, 则tmax= tm+x，故：
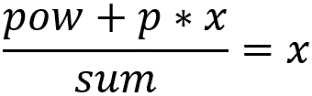
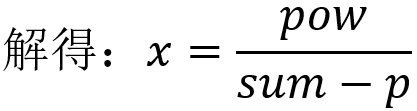
下面用数据来解释一下吧： 第一组数据： 2 1 2 2 2 1000 首先求：a1+a2+……+an=4，而p=1<4=a1+a2+……+an，因此不能用无限长的时间。 把所有设备在不充电时能用的时间算出来： 第一个设备能用2/2=1s，t1=1s, a1=2 第二个设备能用1000/2=500s，t2=500s, a2=2 排序后： t1=1s, a1=2 t2=500s, a2=2 此时充电宝电力为pow=t1*p=1 先充第1个设备(m=1)，此时sum=a1=2，由于pow + (t2 -t1) * p < (t2 -t1)*sum，所以不能让时间延长至t2，x=pow/(sum-p)=1/1=1s，故tmax= tm+x=1+1=2s 所以答案为：2
再看第二组数据： 1 100 1 1 首先求：a1+a2+……+an=1，而p=100>1=a1+a2+……+an，因此能用无限长的时间。输出-1 。
再看第三组数据： 3 5 4 3 5 2 6 1 首先求：a1+a2+……+an=15，而p=5<15=a1+a2+……+an，因此不能用无限长的时间。
把所有设备在不充电时能用的时间算出来： 第一个设备能用3/4=0.75s，t1=0.75s, a1=4 第二个设备能用2/5=0.4s，t2=0.4s, a2=5
第三个设备能用6/1=0.166666666666667s，t3=0.166666666666667s, a3=6
排序后： t1=0.166666666666667s, a1=6
t2=0.4s, a2=5
t3=0.75s, a3=4
此时充电宝电力为pow=t1*p=0.833333333333333 先充第1个设备(m=1)，此时sum=a1=6，由于pow + (t2 -t1) * p > (t2 -t1)*sum ，所以能让时间延长至t2 此时pow=pow（原来的电量）+(tm+1 -tm)*p（这段时间充的电量）- (tm+1 -tm)*sum（让设备1用的时间延长至t2所耗的电量） =pow+ (tm+1 -tm)*(sum-p) 故pow=0.833333333333333+（0.4-0.166666666666667）*（5-6）= 0.6 接着充1-2两个设备(m=2)，此时sum=a1+a2=11，由于pow + (t3 -t2) * p < (t3 -t2)*sum，所以不能让时间延长至t3 此时x=pow/(sum-p)=0.6/6=0.1s 故tmax= t2+x=0.4+0.1=0.5s
附上代码：
#include
using namespace std;
struct In{
long long a;
double t;
}s[100005];
bool cmp(In p, In q) {
return p.t < q.t;
}
int main() {
long long n, p, mid;
scanf("%lld%lld", &n, &p);
long long sum1 = 0;
for(long long i = 0; i < n; i++) {
scanf("%lld%lld", &s[i].a, &mid);
sum1 += s[i].a;
s[i].t = mid * 1.0 / s[i].a;
}
if(sum1 <= p)
printf("-1
");
else {
sort(s, s + n, cmp);
double time = s[0].t;
double pow = s[0].t * p;
double dis, x;
long long sum = s[0].a;
long long i = 1;
while(i < n) {
dis = s[i].t - time;
if(sum > p) {
x = pow / (sum - p);
if(x <= dis) {
printf("%.10f
", time + x);
break;
}
}
pow = pow + dis * (p - sum);
sum += s[i].a;
time = s[i].t;
i++;
}
if(i == n) {
x = pow / (sum - p);
printf("%.10f
", time + x);
}
}
return 0;
}