码一篇灰 {MOD}模型的博客

2019-04-14 18:24发布生成海报

站内文章 / 模拟电子

11872 0

非原创，转载出处 https://blog.csdn.net/WuchangI/article/details/79214882

- 一、灰 {MOD}模型GM(1,1)
- 二、灰 {MOD}Verhulst模型(即Logistic模型)

一、灰 {MOD}模型GM(1,1)

1. 问题

请以下表的数据为依据，预测2005-2014年长江的污水排放量(单位：亿吨)。

1995-2004年的长江污水排放量年份 1995 1996 1997 1998 1999 2000 2001 2002 2003 2004 污水量/亿吨 174 179 183 189 207 234 220.5 256 270 285

2. 分析

此问题为一个复杂的非线性系统，样本数据量少，但需要预测的时间较长，且污水排放量的变化规律是一个不确定的系统。如果使用神经网络算法很难取得理想的效果，故考虑采用GM预测来预测未来的污水排放量。

3. MATLAB实现源代码

GM(1,1).m

%建立符号变量a(发展系数)和b(灰作用量)
syms a b;
c = [a b]';

%原始数列 A
A = [174, 179, 183, 189, 207, 234, 220.5, 256, 270, 285];
n = length(A);

%对原始数列 A 做累加得到数列 B
B = cumsum(A);

%对数列 B 做紧邻均值生成
for i = 2:n
    C(i) = (B(i) + B(i - 1))/2; 
end
C(1) = [];

%构造数据矩阵 
B = [-C;ones(1,n-1)];
Y = A; Y(1) = []; Y = Y';

%使用最小二乘法计算参数 a(发展系数)和b(灰作用量)
c = inv(B*B')*B*Y;
c = c';
a = c(1); b = c(2);

%预测后续数据
F = []; F(1) = A(1);
for i = 2:(n+10)
    F(i) = (A(1)-b/a)/exp(a*(i-1))+ b/a;
end

%对数列 F 累减还原,得到预测出的数据
G = []; G(1) = A(1);
for i = 2:(n+10)
    G(i) = F(i) - F(i-1); %得到预测出来的数据
end

disp('预测数据为：');
G

%模型检验

H = G(1:10);
%计算残差序列
epsilon = A - H;

%法一：相对残差Q检验
%计算相对误差序列
delta = abs(epsilon./A);
%计算相对误差Q
disp('相对残差Q检验：')
Q = mean(delta)

%法二：方差比C检验
disp('方差比C检验：')
C = std(epsilon, 1)/std(A, 1)

%法三：小误差概率P检验
S1 = std(A, 1);
tmp = find(abs(epsilon - mean(epsilon))< 0.6745 * S1);
disp('小误差概率P检验：')
P = length(tmp)/n

%绘制曲线图
t1 = 1995:2004;
t2 = 1995:2014;

plot(t1, A,'ro'); hold on;
plot(t2, G, 'g-');
xlabel('年份'); ylabel('污水量/亿吨');
legend('实际污水排放量','预测污水排放量');
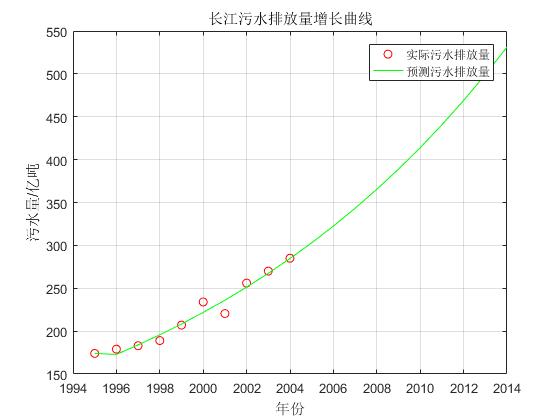
title('长江污水排放量增长曲线');
grid on;

运行结果：

预测数据为： G = 1 至 14 列 174.0000 172.8090 183.9355 195.7785 208.3839 221.8010 236.0820 251.2825 267.4616 284.6825 303.0122 322.5221 343.2881 365.3912 15 至 20 列 388.9175 413.9585 440.6118 468.9812 499.1772 531.3174 相对残差Q检验： Q = 0.0234 方差比C检验： C = 0.1870 小误差概率P检验： P = 1

4. MATLAB绘制的曲线图

二、灰 {MOD}Verhulst模型(即Logistic模型)

1. 问题

将一定量的大肠杆菌菌种接种在液体培养基中，在一定条件下进行培养，观察其生长繁殖规律。细菌悬液的浓度与混浊度成正比，故可用分光亮度计测定细菌悬液的光密度来推知菌液的浓度。每隔5h记录OD600的值，得到下表。请你预测大肠杆菌的数量。

时间点均匀采样/5h 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 细菌培养液吸光度/OD600 0.025 0.023 0.029 0.044 0.084 0.164 0.332 0.521 0.97 1.6 2.45 3.11 3.57 3.76 3.96 4 4.46 4.4 4.49 4.76 5.01

2. 分析

此问题涉及生物的生长和繁殖规律，其曲线一般呈S型或变异S型，故考虑使用GM Verhulst模型来预测。

3. MATLAB实现源代码

（以下程序预测到时间点41）

GM_Verhulst.m

%建立符号变量a(发展系数)和b(灰作用量)
syms a b;
c = [a b]';

%原始数列 A
A = [0.025, 0.023, 0.029, 0.044, 0.084, 0.164, 0.332, 0.521, 0.97, 1.6, 2.45, 3.11, 3.57, 3.76, 3.96, 4, 4.46, 4.4, 4.49, 4.76, 5.01];
n = length(A);

%对原始数列 A 做累减得到数列 B
for i = 2:n
    H(i) = A(i) - A(i - 1);
end
H(1) = [];


%对原始数列 A 做紧邻均值生成
for i = 2:n
    C(i) = (A(i) + A(i-1))/2;
end
C(1) = [];

%构造数据矩阵 
D = [-C; C.^2];
Y = H; Y = Y';

%使用最小二乘法计算参数 a(发展系数)和b(灰作用量)
c = inv(D*D')*D*Y;
c = c';
a = c(1); b = c(2);

%得到预测出的数据
F = []; F(1) = A(1);
for i = 2:(n+n)
    F(i) = (a*A(1))/(b*A(1)+(a - b*A(1))*exp(a*(i-1)));
end

disp('预测数据为：');
F

%绘制曲线图
t1 = 0:n-1; 
t2 = 0:2*n-1;
plot(t1, A, 'ro'); hold on;
plot(t2, F);
xlabel('时间点均匀采样/5h'); ylabel('细菌培养液吸光度/OD600');
legend('实际数量','预测数量');
title('大肠杆菌培养S形增长曲线');
grid on;

运行结果：

预测数据为： F = 1 至 14 列 0.0250 0.0416 0.0691 0.1143 0.1880 0.3059 0.4900 0.7658 1.1551 1.6603 2.2492 2.8555 3.4051 3.8485 15 至 28 列 4.1738 4.3963 4.5412 4.6326 4.6891 4.7236 4.7445 4.7571 4.7647 4.7692 4.7720 4.7736 4.7746 4.7752 29 至 42 列 4.7755 4.7757 4.7759 4.7759 4.7760 4.7760 4.7760 4.7760 4.7760 4.7760 4.7760 4.7760 4.7760 4.7760

4. MATLAB绘制的曲线图

码一篇灰 {MOD}模型的博客

一、灰 {MOD}模型GM(1,1)

1. 问题

2. 分析

3. MATLAB实现源代码

4. MATLAB绘制的曲线图

二、灰 {MOD}Verhulst模型(即Logistic模型)

1. 问题

2. 分析

3. MATLAB实现源代码

4. MATLAB绘制的曲线图

Ta的文章更多 >>

热门文章

码一篇灰 {MOD}模型的博客

一、 灰 {MOD}模型GM(1,1)

1. 问题

2. 分析

3. MATLAB实现源代码

4. MATLAB绘制的曲线图

二、 灰 {MOD}Verhulst模型(即Logistic模型)

1. 问题

2. 分析

3. MATLAB实现源代码

4. MATLAB绘制的曲线图

Ta的文章 更多 >>

热门文章

举报内容

检举类型

检举原因

检举说明(必填)

打开微信“扫一扫”，打开网页后点击屏幕右上角分享按钮

一、灰 {MOD}模型GM(1,1)

二、灰 {MOD}Verhulst模型(即Logistic模型)

Ta的文章更多 >>