中国剩余定理(CRT)的表述如下
设正整数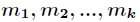 两两互素,则同余方程组
两两互素,则同余方程组
 有整数解。并且在模
有整数解。并且在模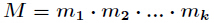 下的解是唯一的,解为
下的解是唯一的,解为
 其中
其中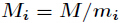 ,而
,而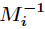 为
为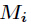 模
模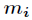 的逆元。
代码:
的逆元。
代码:
题目:http://poj.org/problem?id=1006 题意:人自出生起就有体力,情感和智力三个生理周期,分别为23,28和33天。一个周期内有一天为峰值,在这一 天,人在对应的方面(体力,情感或智力)表现最好。通常这三个周期的峰值不会是同一天。现在给出三个日 期,分别对应于体力,情感,智力出现峰值的日期。然后再给出一个起始日期,要求从这一天开始,算出最少 再过多少天后三个峰值同时出现。 代码:
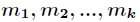 两两互素,则同余方程组
两两互素,则同余方程组
 有整数解。并且在模
有整数解。并且在模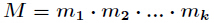 下的解是唯一的,解为
下的解是唯一的,解为
 其中
其中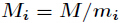 ,而
,而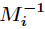 为
为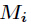 模
模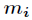 的逆元。
代码:
的逆元。
代码:
int CRT(int a[],int m[],int n)
{
int M = 1;
int ans = 0;
for(int i=1; i<=n; i++)
M *= m[i];
for(int i=1; i<=n; i++)
{
int x, y;
int Mi = M / m[i];
extend_Euclid(Mi, m[i], x, y);
ans = (ans + Mi * x * a[i]) % M;
}
if(ans < 0) ans += M;
return ans;
} 题目:http://poj.org/problem?id=1006 题意:人自出生起就有体力,情感和智力三个生理周期,分别为23,28和33天。一个周期内有一天为峰值,在这一 天,人在对应的方面(体力,情感或智力)表现最好。通常这三个周期的峰值不会是同一天。现在给出三个日 期,分别对应于体力,情感,智力出现峰值的日期。然后再给出一个起始日期,要求从这一天开始,算出最少 再过多少天后三个峰值同时出现。 代码:
#include
#include
#include
using namespace std;
int a[4], m[4];
void extend_Euclid(int a, int b, int &x, int &y)
{
if(b == 0)
{
x = 1;
y = 0;
return;
}
extend_Euclid(b, a % b, x, y);
int tmp = x;
x = y;
y = tmp - (a / b) * y;
}
int CRT(int a[],int m[],int n)
{
int M = 1;
int ans = 0;
for(int i=1; i<=n; i++)
M *= m[i];
for(int i=1; i<=n; i++)
{
int x, y;
int Mi = M / m[i];
extend_Euclid(Mi, m[i], x, y);
ans = (ans + Mi * x * a[i]) % M;
}
if(ans < 0) ans += M;
return ans;
}
int main()
{
int p, e, i, d, t = 1;
while(cin>>p>>e>>i>>d)
{
if(p == -1 && e == -1 && i == -1 && d == -1)
break;
a[1] = p;
a[2] = e;
a[3] = i;
m[1] = 23;
m[2] = 28;
m[3] = 33;
int ans = CRT(a, m, 3);
if(ans <= d)
ans += 21252;
cout<<"Case "<
普通的中国剩余定理要求所有的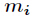 互素,那么如果不互素呢,怎么求解同余方程组?
这种情况就采用两两合并的思想,假设要合并如下两个方程
互素,那么如果不互素呢,怎么求解同余方程组?
这种情况就采用两两合并的思想,假设要合并如下两个方程
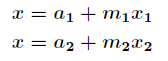 那么得到
那么得到
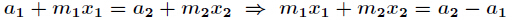 在利用扩展欧几里得算法解出
在利用扩展欧几里得算法解出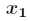 的最小正整数解,再带入
的最小正整数解,再带入
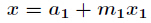 得到
得到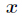 后合并为一个方程的结果为
后合并为一个方程的结果为
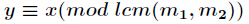 这样一直合并下去,最终可以求得同余方程组的解。
题目:http://poj.org/problem?id=2891
代码:
这样一直合并下去,最终可以求得同余方程组的解。
题目:http://poj.org/problem?id=2891
代码:
#include
#include
#include
using namespace std;
typedef long long LL;
const int N = 1005;
LL a[N], m[N];
LL gcd(LL a,LL b)
{
return b? gcd(b, a % b) : a;
}
void extend_Euclid(LL a, LL b, LL &x, LL &y)
{
if(b == 0)
{
x = 1;
y = 0;
return;
}
extend_Euclid(b, a % b, x, y);
LL tmp = x;
x = y;
y = tmp - (a / b) * y;
}
LL Inv(LL a, LL b)
{
LL d = gcd(a, b);
if(d != 1) return -1;
LL x, y;
extend_Euclid(a, b, x, y);
return (x % b + b) % b;
}
bool merge(LL a1, LL m1, LL a2, LL m2, LL &a3, LL &m3)
{
LL d = gcd(m1, m2);
LL c = a2 - a1;
if(c % d) return false;
c = (c % m2 + m2) % m2;
m1 /= d;
m2 /= d;
c /= d;
c *= Inv(m1, m2);
c %= m2;
c *= m1 * d;
c += a1;
m3 = m1 * m2 * d;
a3 = (c % m3 + m3) % m3;
return true;
}
LL CRT(LL a[], LL m[], int n)
{
LL a1 = a[1];
LL m1 = m[1];
for(int i=2; i<=n; i++)
{
LL a2 = a[i];
LL m2 = m[i];
LL m3, a3;
if(!merge(a1, m1, a2, m2, a3, m3))
return -1;
a1 = a3;
m1 = m3;
}
return (a1 % m1 + m1) % m1;
}
int main()
{
int n;
while(scanf("%d",&n)!=EOF)
{
for(int i=1; i<=n; i++)
scanf("%I64d%I64d",&m[i], &a[i]);
LL ans = CRT(a, m, n);
printf("%I64d
",ans);
}
return 0;
}
题目:http://acm.hdu.edu.cn/showproblem.php?pid=1573
分析:这个题由于数据范围小,那么直接可以通过枚举在这 个数的最小公倍数范围内的所有数,找到最小的正整
数解,然后后面的所有解都可以通过这个得到。
代码:
个数的最小公倍数范围内的所有数,找到最小的正整
数解,然后后面的所有解都可以通过这个得到。
代码:
#include
#include
#include
using namespace std;
const int N = 25;
int a[N], b[N];
int gcd(int a, int b)
{
return b ? gcd(b, a % b) : a;
}
int main()
{
int T;
cin>>T;
while(T--)
{
int n, m;
cin>>n>>m;
for(int i=0; i>a[i];
for(int i=0; i>b[i];
int lcm = 1;
for(int i=0; i