模型矩阵在webgl中表示 模型的缩放 旋转 平移的所以模型矩阵包含了 旋转矩阵:
缩放矩阵:
平移矩阵:
下面给出一份演示:
变量mM在上面的列子中表示模型矩阵
在学习之前应该先了解一下矩阵相乘的概念: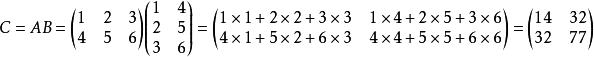
可以看到是行乘以列得到新的行和列
webgl中我们采用一维数组表示矩阵.那么问题来了 这个一维数组的前四个元素是表示列还是行啦?在webgl中前四个元素表示列
设模型矩阵的位置关系是这样的[0,1,2,3,4,5,6,7,8,9,10,11,12,13,14,15]
下面来逐一介绍各个函数:
rotateX 沿着X轴旋转的旋转矩阵其实就是沿着X轴旋转的矩阵乘以 模型矩阵最后得到一个新的矩阵因为webgl中前四个元素表示列所以我们用X轴旋转矩阵乘以模型矩阵的前四个元素就表示行乘以列了最终得到mM[0] =c*mM[1] - s*mM[2];因为webgl中前四个元素表示列所以mM[1]就不是第一行的元素了 mM[4]才是第一行的第二个元素 所以得到 mM[5] = c*mM[5] - s*mM[6];
还是同上面的理由可以得到mM[9] = c*mM[9] - s*mM[10];
rotateX旋转的方法就到这里介绍完毕了 rotateY和rotateZ都可以经过上面的原理进行推理得到结果
下面介绍moveX方法moveX方法其实是平移矩阵乘以模型矩阵然后得到一个新的矩阵根据上面平移矩阵的信息可以知道我们如果以X轴移动那么就有这样的矩阵[ 1,0,0,x,
0,1,0,0, 0,0,1,0,
0,0,0,1
]根据矩阵相乘的原理和webgl数组前四个元素表示列的原理可以知道
moveY 方法:moveY其实是矩阵[ 1,0,0,0,
0,1,0,y, 0,0,1,0,
0,0,0,1
]乘以模型矩阵得到结果以此类推可以知道moveZ的结果了吧
下面介绍scaleFun的原理缩放函数其实是缩放矩阵乘以模型矩阵然后得到一个新的矩阵[ x,0,0,0, 0,y,0,0,
0,0,z,0,
0,0,0,1
]为什么缩放矩阵X Y Z都是在一个方法里面执行的拉 是因为楼主在写的时候 写了scaleX 和scaleY ,scaleZ 但是发现模型变形了所以就将缩放矩阵放到一起 就得到上面的结果 原来缩放要一起缩放
下面说下为什么在执行了方法过后 即mM数组改变了 模型为什么会改变是因为楼主在演示的最后加一个requestAnimationFrame方法 让模型一直在更新 并把mM数组赋值到着 {MOD}器语言的mat变量里面

缩放矩阵:

平移矩阵:

下面给出一份演示:
上面的演示演示了 模型矩阵的一些使用我们知道模型矩阵*vec4这个表示顶点的信息变量mM在上面的列子中表示模型矩阵
在学习之前应该先了解一下矩阵相乘的概念:
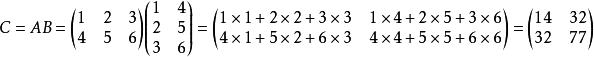
可以看到是行乘以列得到新的行和列
webgl中我们采用一维数组表示矩阵.那么问题来了 这个一维数组的前四个元素是表示列还是行啦?在webgl中前四个元素表示列
设模型矩阵的位置关系是这样的[0,1,2,3,4,5,6,7,8,9,10,11,12,13,14,15]
下面来逐一介绍各个函数:
rotateX 沿着X轴旋转的旋转矩阵其实就是沿着X轴旋转的矩阵乘以 模型矩阵最后得到一个新的矩阵因为webgl中前四个元素表示列所以我们用X轴旋转矩阵乘以模型矩阵的前四个元素就表示行乘以列了最终得到mM[0] =c*mM[1] - s*mM[2];因为webgl中前四个元素表示列所以mM[1]就不是第一行的元素了 mM[4]才是第一行的第二个元素 所以得到 mM[5] = c*mM[5] - s*mM[6];
还是同上面的理由可以得到mM[9] = c*mM[9] - s*mM[10];
rotateX旋转的方法就到这里介绍完毕了 rotateY和rotateZ都可以经过上面的原理进行推理得到结果
下面介绍moveX方法moveX方法其实是平移矩阵乘以模型矩阵然后得到一个新的矩阵根据上面平移矩阵的信息可以知道我们如果以X轴移动那么就有这样的矩阵[ 1,0,0,x,
0,1,0,0, 0,0,1,0,
0,0,0,1
]根据矩阵相乘的原理和webgl数组前四个元素表示列的原理可以知道
mM[0]=mM[0]+distance*mM[3];
mM[4]=mM[4]+distance*mM[7];
mM[8]=mM[8]+distance*mM[11];
mM[12]=mM[12]+distance*mM[15];矩阵相乘的结果moveY 方法:moveY其实是矩阵[ 1,0,0,0,
0,1,0,y, 0,0,1,0,
0,0,0,1
]乘以模型矩阵得到结果以此类推可以知道moveZ的结果了吧
下面介绍scaleFun的原理缩放函数其实是缩放矩阵乘以模型矩阵然后得到一个新的矩阵[ x,0,0,0, 0,y,0,0,
0,0,z,0,
0,0,0,1
]为什么缩放矩阵X Y Z都是在一个方法里面执行的拉 是因为楼主在写的时候 写了scaleX 和scaleY ,scaleZ 但是发现模型变形了所以就将缩放矩阵放到一起 就得到上面的结果 原来缩放要一起缩放
下面说下为什么在执行了方法过后 即mM数组改变了 模型为什么会改变是因为楼主在演示的最后加一个requestAnimationFrame方法 让模型一直在更新 并把mM数组赋值到着 {MOD}器语言的mat变量里面