题目描述:
时间限制:10000ms
单点时限:1000ms
内存限制:256MB
例如: f(3214567) = 3 - 2 + 1 - 4 + 5 - 6 + 7 = 4
给定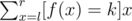
Output 611668829
Input 404491953 1587197241 1
Output 323937411
Input 60296763086567224 193422344885593844 10
Output 608746132 Input 100 121 -1
Output 120
样例输入 100 121 0 样例输出 231 解题思路: 这道题确实花了我好几天的时间来做。。首先,根据题目的意思,我尝试列举几个样例来得到一般规律,但处处因为各种原因(比如说当在某一位发生进位时。。),导致分析过程异常复杂,而且情况也多种多样,最后不得已,只好放弃找规律这条路。理所当然地,一般规律找不到,就只有暴力来解决,下面是代码:
当然了,这个代码是超时的,当它在我后面的调试中起到很重要的作用!(输出结果,用excel来处理,看看与自己代码输出是否一致) 现在来仔细分析这个代码的复杂度,可以粗略地认为它的时间复杂度为O(n),n为输入的值,可以看到n可以达到10^20的数量级,这确实是很难被接受的,不得已,在网上搜了下,发现这道题是用数位dp来做的,由于之前没怎么接触过,所以就找了道题做了下,做完之后,再来看这道题,就基本有思路了,所以就尝试开始做,这里我采用的是非递归方法,所以会比递归的dfs来做看起来会复杂点,这在之前已经讨论过了,基本思路如下: dpSum[i][j] 表示长度为i,交错和为j的数的和(注意,这里的数可以以0开头,否则就会少算一些值,例如当确定了最高位是1后,其余i-1位可以以0开头) dpCnt[i][j] 表示长度为i, 交错和是j的数的个数 由于交错和可以是负数,所以为其加上100,保证其为正数,状态转移方程为:(在程序中要注意溢出问题,这里为了便于理解,就省去了取模操作) dpSum[i][j] += dpSum[i-1][200-(j-k)] + k * sz[i] * dpCnt[i-1][200-(j-k)] 其中k取0到9,表示第i位可能的取值,200-(j-k)表示当前的交错和减去第i位的值再取反,sz[n]表示位数为n的最小的数(这里将其作为基底),即当n为2时,sz[n]为10, dpCnt[i][j] += dpCnt[i][200-(j-k)]; 初始状态是:dpCnt[0][0] = 1(这一点很重要),然后将长度为1的值都初始化就可以了。 求完dp数组后,就可以求具体的值了,这里用了个cal函数long long cal(long long n, int target) 表示求0到n-1的交错和为k的数的和: 首先先求出位数少于n的位数的结果, 然后求位数等于n的位数的数的和: res += dpSum[i-1][200-(target-k)] + (n-n%sz[i+1]+k*sz[i]) * dpCnt[i-1][200-(target-k)] ;
其中 (n-n%sz[i+1]+k*sz[i]) 求出的是该数的比i高的位,和以k作为第i位的数,例如1234567,i = 5,k = 2则这里表示1220000。 整体代码如下,
当然,这道题也可以用递归来做: 其中,主要注意dp[i][j]保存的是不考虑上下界,且可以以0开头的i位数,其交错和是j的数的和与个数;
描述
给定一个数 x,设它十进制展从高位到低位上的数位依次是 a0, a1, ..., an - 1,定义交错和函数: f(x) = a0 - a1 + a2 - ... + ( - 1)n - 1an - 1例如: f(3214567) = 3 - 2 + 1 - 4 + 5 - 6 + 7 = 4
给定
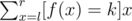
输入
输入数据仅一行包含三个整数,l, r, k(0 ≤ l ≤ r ≤ 1018, |k| ≤ 100)。输出
输出一行一个整数表示结果,考虑到答案可能很大,输出结果模 109 + 7。提示
对于样例 ,满足条件的数有 110 和 121,所以结果是 231 = 110 + 121。 更多样例: Input 4344 3214567 3Output 611668829
Input 404491953 1587197241 1
Output 323937411
Input 60296763086567224 193422344885593844 10
Output 608746132 Input 100 121 -1
Output 120
样例输入 100 121 0 样例输出 231 解题思路: 这道题确实花了我好几天的时间来做。。首先,根据题目的意思,我尝试列举几个样例来得到一般规律,但处处因为各种原因(比如说当在某一位发生进位时。。),导致分析过程异常复杂,而且情况也多种多样,最后不得已,只好放弃找规律这条路。理所当然地,一般规律找不到,就只有暴力来解决,下面是代码:
#include
#include
#include
using namespace std;
int MOD = 1e9+7;
/*int cross_sum(long long t){
int res = 0;
strstream ss;
ss << t;
string num;
ss >> num;
int flag = 1;
for(int i = 0; i < num.size(); i++){
res += flag * (num[i] - '0');
flag = -flag;
}
return res;
}*/
int cross_sum(long long t){
int res = 0, flag = 1;
while(t > 0){
res += flag * (t % 10);
t = t/10;
flag = -flag;
}
if(flag > 0)
res = -res;
return res;
}
int main(){
//freopen("t.txt", "r", stdin);
long long left, right;
int k;
scanf("%lld%lld%d", &left, &right, &k);
long long res = 0, base = left;
for(; base <= right; base++){
if(cross_sum(base) == k){
res = (res + base) % MOD;
}
}
printf("%lld
", res);
return 0;
}
当然了,这个代码是超时的,当它在我后面的调试中起到很重要的作用!(输出结果,用excel来处理,看看与自己代码输出是否一致) 现在来仔细分析这个代码的复杂度,可以粗略地认为它的时间复杂度为O(n),n为输入的值,可以看到n可以达到10^20的数量级,这确实是很难被接受的,不得已,在网上搜了下,发现这道题是用数位dp来做的,由于之前没怎么接触过,所以就找了道题做了下,做完之后,再来看这道题,就基本有思路了,所以就尝试开始做,这里我采用的是非递归方法,所以会比递归的dfs来做看起来会复杂点,这在之前已经讨论过了,基本思路如下: dpSum[i][j] 表示长度为i,交错和为j的数的和(注意,这里的数可以以0开头,否则就会少算一些值,例如当确定了最高位是1后,其余i-1位可以以0开头) dpCnt[i][j] 表示长度为i, 交错和是j的数的个数 由于交错和可以是负数,所以为其加上100,保证其为正数,状态转移方程为:(在程序中要注意溢出问题,这里为了便于理解,就省去了取模操作) dpSum[i][j] += dpSum[i-1][200-(j-k)] + k * sz[i] * dpCnt[i-1][200-(j-k)] 其中k取0到9,表示第i位可能的取值,200-(j-k)表示当前的交错和减去第i位的值再取反,sz[n]表示位数为n的最小的数(这里将其作为基底),即当n为2时,sz[n]为10, dpCnt[i][j] += dpCnt[i][200-(j-k)]; 初始状态是:dpCnt[0][0] = 1(这一点很重要),然后将长度为1的值都初始化就可以了。 求完dp数组后,就可以求具体的值了,这里用了个cal函数long long cal(long long n, int target) 表示求0到n-1的交错和为k的数的和: 首先先求出位数少于n的位数的结果, 然后求位数等于n的位数的数的和: res += dpSum[i-1][200-(target-k)] + (n-n%sz[i+1]+k*sz[i]) * dpCnt[i-1][200-(target-k)] ;
其中 (n-n%sz[i+1]+k*sz[i]) 求出的是该数的比i高的位,和以k作为第i位的数,例如1234567,i = 5,k = 2则这里表示1220000。 整体代码如下,
#include
#include
#include
using namespace std;
const int N = 22, MAX = 209, MOD = 1e9+7;
long long dpSum[N][MAX], dpCnt[N][MAX], sz[N] = {0,1};
void init(){
memset(dpSum, 0, sizeof(dpSum));
memset(dpCnt, 0, sizeof(dpCnt));
for(int i = 2; i < N; i++){
sz[i] = sz[i-1] * 10;
}
dpCnt[0][100] = 1;
for(int i = 0; i <= 9; i++){
dpSum[1][100+i] = i;
dpCnt[1][100+i] = 1;
}
for(int i = 2; i < N; i++){
for(int j = 0; j <= 200; j++){
for(int k = 0; k <= 9; k++){
dpSum[i][j] += (dpSum[i-1][200-(j - k)]
+ k * sz[i] % MOD * dpCnt[i-1][200-(j - k)])%MOD;
dpSum[i][j] %= MOD;
dpCnt[i][j] += dpCnt[i-1][200-(j - k)];
dpCnt[i][j] %= MOD;
}
}
}
}
long long cal(long long n, int target){
if(n == -1)
return 0;
int numArray[N], len = 0;
long long tmp = n;
while(tmp){
numArray[++len] = tmp % 10;
tmp /= 10;
}
long long res = 0;
//先求出满足条件的位数小于n的数字的和
for(int i = 1; i < len; i++){
for(int k = 1; k <= 9; k++){
res += ( dpSum[i-1][200-(target-k)]
+ k * sz[i] % MOD * dpCnt[i-1][200-(target-k)] % MOD ) % MOD;
res %= MOD;
}
}
//求位数等于n的位数的满足条件的数字和
for(int i = len; i > 0; i--){
int k = (i == len);
for(; k < numArray[i];k++){
res += (dpSum[i-1][200-(target-k)]
+ (n-n%sz[i+1]+k*sz[i]) % MOD * dpCnt[i-1][200-(target-k)] % MOD ) % MOD;
res %= MOD;
}
target = 200 - (target - numArray[i]);
}
return res;
}
int main(){
//freopen("t.txt", "r", stdin);
init();
long long left, right;
int k;
scanf("%lld%lld%d", &left, &right, &k);
long long res = cal(right+1, k+100) - cal(left, k+100);
if(res < 0)
res += MOD;
res %= MOD;
printf("%lld
", res);
return 0;
}
当然,这道题也可以用递归来做: 其中,主要注意dp[i][j]保存的是不考虑上下界,且可以以0开头的i位数,其交错和是j的数的和与个数;
node dfs(int pos, int target, int hasCeiling, int len)返回的是在长度为len,从0到pos位,交错和为target的数的和与个数
#include
#include
#include
using namespace std;
const int N = 22, MAX = 209, MOD = 1e9+7;
long long base[N] = {0,1};
int numArray[N];
struct node{
long long sum, cnt;
node():sum(-1), cnt(-1){}
};
node dp[N][MAX];
node dfs(int pos, int target, int hasCeiling, int len){
node res;
res.sum = res.cnt = 0;
if(pos == 0){
if(target == 100)
res.cnt = 1;
return res;
}
//注意dp中保存的是没有上下限限制,且开头可以为0的数
if(!hasCeiling && len != pos && dp[pos][target].cnt != -1)
return dp[pos][target];
int head = (len == pos);
int tail = hasCeiling ? numArray[pos] : 9;
for(int i = head; i <= tail; i++){
node tmp = dfs(pos-1, 200-(target-i), hasCeiling && i==numArray[pos], len);
if(tmp.cnt > 0){
res.cnt += tmp.cnt;
res.cnt %= MOD;
res.sum += tmp.sum;
res.sum %= MOD;
res.sum += (tmp.cnt * i * base[pos]) % MOD;
res.sum %= MOD;
}
}
if(!hasCeiling && len != pos){
dp[pos][target] = res;
}
return res;
}
long long cal(long long n, int k){
if(n == -1)
return 0;
int len = 0;
while(n){
numArray[++len] = n % 10;
n /= 10;
}
long long ans = 0;
node tmp;
for(int i = 1; i <= len; i++){
tmp = dfs(i, k, i == len, i);
ans += tmp.sum;
ans %= MOD;
}
return ans;
}
int main(){
//freopen("t.txt", "r", stdin);
for(int i = 2; i < N; i++)
base[i] = base[i-1] * 10 % MOD;
long long left, right;
int k;
scanf("%lld%lld%d", &left, &right, &k);
/*
cout << cal(right, k+100) << endl;
cout << cal(left-1, k+100) << endl;
*/
printf("%lld
", (cal(right, k+100) - cal(left-1, k+100) + MOD) % MOD );
return 0;
}