class="markdown_views prism-tomorrow-night">
2)调用模型进行实时监测
1.从电力计量自动化系统、营销系统有选择性地抽取部分大用户用电负荷、终端报警及违约窃电处罚信息等原始数据。
2.剔除白名单用户,即不可能存在漏电的用户。描述性和探索性分析正常用户和窃漏电用户的用电特征。
3.处理样本缺失值,通过经验构建特征指标,形成专家数据集
4.构建窃漏电用户识别模型
5.模型落地,在线监测用户用电负荷及终端报警,调用模型实现实时诊断。
6.通过对诊断结果的评估,优化或者重构模型


2.周期分析:
正常用电电量探索分析(平稳)

窃漏电用电电量探索分析(明显下降)

剔除白名单用户,这里把这些用户归为非居民类别
剔除节假日用电数据,根据业务经验节假日用电量明显偏低(大部分用户为企业用户)
2.缺失值处理
如果直接将缺失值剔除,会严重影响供出电量的计算结果,从而导致日线损率误差很大,故本案例采用拉格朗日插值法对缺失值填补。
拉格朗日插补可以选取缺失值前后5个数据或者和邻近缺失值之间的所有数据,组成一组,使用如下公式:

需要通过新的评价指标来表征窃漏电用户的行为规律,故根据业务经验和专业理论引出三个评价指标:电量趋势下降指标、线损指标、告警类指标
电量趋势下降指标:取统计当天及前后五天共11天的数据,通过线性拟合计算斜率,如果当天的斜率小于前一天的,则计数加1,可以据此计算敏感时期内的总计数。
线损指标:线损率具体查看相关电学知识,取当天及前五天线损均值,当天及后五天线损均值比较,如果增长率大于1%,则记为1,否则为0
告警类指标:取自终端报警次数总和

2.数据清洗及转换:通过作图在时间维度上查看前后5天内的电量均值变化趋势;计算电量下降趋势指标;计算线损指标
3.数据划分:划分训练样本和测试样本,方便比对模型的有效性
4.神经网络建模:运用较为简单的BP神经网络建立分类模型
5.构建CART决策树模型
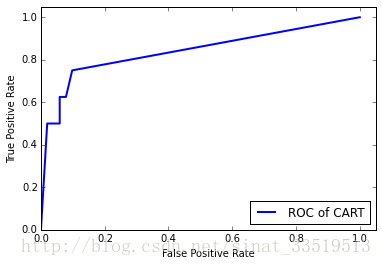
6.模型评价:利用ROC曲线在测试集上评价模型
1.挖掘目标
1)归纳出窃漏电用户的关键特征,构建窃漏电用户的识别模型;2)调用模型进行实时监测
2 分析方法与过程
要剔除不可能存在漏电的大用户,如银行、税务、学校、工商。用电负荷随着时间的变化才有价值,而终端报警存在误报和漏报,而这些数据都能够帮助总结用户窃漏电的行为规律,即通过预处理提炼出描述用户窃漏电特征的相关指标,最终得到建模使用的专家样本数据集,然后开始建模等工作。主要步骤如下:1.从电力计量自动化系统、营销系统有选择性地抽取部分大用户用电负荷、终端报警及违约窃电处罚信息等原始数据。
2.剔除白名单用户,即不可能存在漏电的用户。描述性和探索性分析正常用户和窃漏电用户的用电特征。
3.处理样本缺失值,通过经验构建特征指标,形成专家数据集
4.构建窃漏电用户识别模型
5.模型落地,在线监测用户用电负荷及终端报警,调用模型实现实时诊断。
6.通过对诊断结果的评估,优化或者重构模型

3数据探索分析
1.分布分析
2.周期分析:
正常用电电量探索分析(平稳)

窃漏电用电电量探索分析(明显下降)

4数据预处理
1.数据清洗:剔除白名单用户,这里把这些用户归为非居民类别
剔除节假日用电数据,根据业务经验节假日用电量明显偏低(大部分用户为企业用户)
2.缺失值处理
如果直接将缺失值剔除,会严重影响供出电量的计算结果,从而导致日线损率误差很大,故本案例采用拉格朗日插值法对缺失值填补。
拉格朗日插补可以选取缺失值前后5个数据或者和邻近缺失值之间的所有数据,组成一组,使用如下公式:

# -*- coding: utf-8 -*-
"""
Created on Thu May 31 10:29:34 2018
@author: lixu
"""
# 拉格朗日插值
import pandas as pd
from scipy.interpolate import lagrange
inputfile = 'eeeee/chapter6/test/data/missing_data.xls'
outputfile = 'eeeee/chapter6/test/data/missing_data_processed.xls'
data = pd.read_excel(inputfile, header=None)
print data
# 自定义插值函数
# s为列向量,n为被插值的位置,k为取前后的数据个数,默认5
def ployinterp_column(s, n, k=5):
y = s[list(range(n-k, n)) + list(range(n+1, n+1+k))]
y = y[y.notnull()]
return lagrange(y.index, list(y))(n)
# 逐个元素判断是否需要插值
for i in data.columns:
for j in range(len(data)):
if (data[i].isnull())[j]:
data[i][j] = ployinterp_column(data[i], j)
data.to_excel(outputfile, header=None, index=False)
print data
"""
原始数据
0 1 2
0 235.8333 324.0343 478.3231
1 236.2708 325.6379 515.4564
2 238.0521 328.0897 517.0909
3 235.9063 NaN 514.8900
4 236.7604 268.8324 NaN
5 NaN 404.0480 486.0912
6 237.4167 391.2652 516.2330
7 238.6563 380.8241 NaN
8 237.6042 388.0230 435.3508
9 238.0313 206.4349 487.6750
10 235.0729 NaN NaN
11 235.5313 400.0787 660.2347
12 NaN 411.2069 621.2346
13 234.4688 395.2343 611.3408
14 235.5000 344.8221 643.0863
15 235.6354 385.6432 642.3482
16 234.5521 401.6234 NaN
17 236.0000 409.6489 602.9347
18 235.2396 416.8795 589.3457
19 235.4896 NaN 556.3452
20 236.9688 NaN 538.3470
插值后
0 1 2
0 235.833300 324.034300 478.323100
1 236.270800 325.637900 515.456400
2 238.052100 328.089700 517.090900
3 235.906300 203.462116 514.890000
4 236.760400 268.832400 493.352591
5 237.151181 404.048000 486.091200
6 237.416700 391.265200 516.233000
7 238.656300 380.824100 493.342382
8 237.604200 388.023000 435.350800
9 238.031300 206.434900 487.675000
10 235.072900 237.348072 609.193564
11 235.531300 400.078700 660.234700
12 235.314951 411.206900 621.234600
13 234.468800 395.234300 611.340800
14 235.500000 344.822100 643.086300
15 235.635400 385.643200 642.348200
16 234.552100 401.623400 618.197198
17 236.000000 409.648900 602.934700
18 235.239600 416.879500 589.345700
19 235.489600 420.748600 556.345200
20 236.968800 408.963200 538.347000
"""
3.数据变换 需要通过新的评价指标来表征窃漏电用户的行为规律,故根据业务经验和专业理论引出三个评价指标:电量趋势下降指标、线损指标、告警类指标
电量趋势下降指标:取统计当天及前后五天共11天的数据,通过线性拟合计算斜率,如果当天的斜率小于前一天的,则计数加1,可以据此计算敏感时期内的总计数。
线损指标:线损率具体查看相关电学知识,取当天及前五天线损均值,当天及后五天线损均值比较,如果增长率大于1%,则记为1,否则为0
告警类指标:取自终端报警次数总和

5模型构建
数据预处理
# 数据划分
from random import shuffle#打乱数据
datafile = 'eeeee/chapter6/test/data/model.xls'
data = pd.read_excel(datafile).as_matrix()
shuffle(data)
p = 0.8
train = data[:int(len(data)*p), :]
test = data[int(len(data)*p), :]
LM神经网络
from keras.models import Sequential
from keras.layers.core import Dense, Activation
netfile = 'eeeee/chapter6/test/data/net.model'
net = Sequential()
net.add(Dense(3, 10))
net.add(Activation('relu'))
net.add(Dense(10, 1))
net.add(Activation('sigmoid'))
net.compile(loss='binary_crossentropy', optimizer='adam', class_mode='binary')
net.fit(train[:, :3], train[:, 3], nb_epoch=1000, batch_size=1)
net.save_weights(netfile)
predict_result = net.predict_classes(train[:,:3]).reshape(len(train))
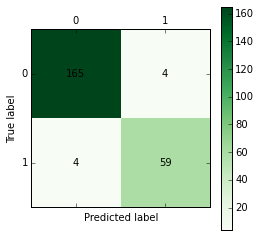
def cm_plot(y, yp):
from sklearn.metrics import confusion_matrix #导入混淆矩阵函数
cm = confusion_matrix(y, yp) #混淆矩阵
import matplotlib.pyplot as plt #导入作图库
plt.matshow(cm, cmap=plt.cm.Greens) #画混淆矩阵图,配 {MOD}风格使用cm.Greens,更多风格请参考官网。
plt.colorbar() #颜 {MOD}标签
for x in range(len(cm)): #数据标签
for y in range(len(cm)):
plt.annotate(cm[x,y], xy=(x, y), horizontalalignment='center', verticalalignment='center')
plt.ylabel('True label') #坐标轴标签
plt.xlabel('Predicted label') #坐标轴标签
return plt
cm_plot(train[:,3], predict_result).show()
CART决策树
from sklearn.tree import DecisionTreeClassifier
tree = DecisionTreeClassifier() #建立决策树模型
#对模型进行训练
tree.fit(train[:,:3], train[:,3])
cm_plot(test[:,3], tree.predict(test[:,:3])).show()

ROC曲线
from sklearn.metrics import roc_curve
import matplotlib.pyplot as plt
#fpr即上文提到的假正例率,tpr即上文提到过的真正例率,分别为ROC曲线的横纵坐标,而predic_proba是预测每个分类的概率
fpr, tpr, thresholds = roc_curve(data_test[:,3], tree.predict_proba(data_test[:,:3])[:,1], pos_label=1)
#作出ROC曲线
plt.plot(fpr, tpr, linewidth=2, label = 'ROC of CART', color = 'blue')
#x轴标签
plt.xlabel('False Positive Rate')
#y轴标签
plt.ylabel('True Positive Rate')
#y轴范围
plt.ylim(0,1.05)
#x轴范围
plt.xlim(0,1.05)
#图例
plt.legend(loc=4)
plt.show()

本案例共包含五个知识点
1.拉格朗日插值法:使用拉格朗日填补法填补缺失值2.数据清洗及转换:通过作图在时间维度上查看前后5天内的电量均值变化趋势;计算电量下降趋势指标;计算线损指标
3.数据划分:划分训练样本和测试样本,方便比对模型的有效性
4.神经网络建模:运用较为简单的BP神经网络建立分类模型
5.构建CART决策树模型
6.模型评价:利用ROC曲线在测试集上评价模型