原文http://blog.csdn.net/jinshengtao/article/details/26278725 前些日子一直在忙答辩的事情，毕业后去了华为，图像处理什么的都派不上用场了。打算分3-4篇文章，把我研究生阶段学过的常用算法为大家和4107的师弟师妹们分享下。本次介绍混合高斯背景建模算法，还是老样子，首先介绍理论部分，然后给出代码，最后实验贴图。 一、理论 混合高斯背景建模是基于像素样本统计信息的背景表示方法，利用像素在较长时间内大量样本值的概率密度等统计信息(如模式数量、每个模式的均值和标准差)表示背景，然后使用统计差分(如3σ原则)进行目标像素判断，可以对复杂动态背景进行建模，计算量较大。 在混合高斯背景模型中，认为像素之间的颜 {MOD}信息互不相关，对各像素点的处理都是相互独立的。对于视频图像中的每一个像素点，其值在序列图像中的变化可看作是不断产生像素值的随机过程，即用高斯分布来描述每个像素点的颜 {MOD}呈现规律【单模态(单峰)，多模态(多峰)】。 对于多峰高斯分布模型，图像的每一个像素点按不同权值的多个高斯分布的叠加来建模，每种高斯分布对应一个可能产生像素点所呈现颜 {MOD}的状态，各个高斯分布的权值和分布参数随时间更新。当处理彩 {MOD}图像时，假定图像像素点R、G、B三 {MOD}通道相互独立并具有相同的方差。对于随机变量X的观测数据集{x1,x2,…,xN}，xt=(rt,gt,bt)为t时刻像素的样本，则单个采样点xt其服从的混合高斯分布概率密度函数：

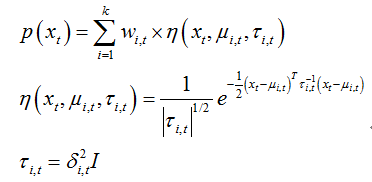
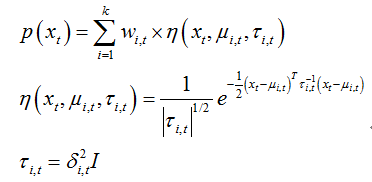
其中k为分布模式总数，η(xt,μi,t, τi,t)为t时刻第i个高斯分布，μi,t为其均值，τi,t为其协方差矩阵，δi,t为方差，I为三维单位矩阵，ωi,t为t时刻第i个高斯分布的权重。 详细算法流程：


二、代码实现 // my_mixgaussians.cpp : 定义控制台应用程序的入口点。 // #include "stdafx.h" #include "cv.h" #include "highgui.h" int _tmain(int argc, _TCHAR* argv[]) { CvCapture *capture=cvCreateFileCapture("test.avi"); IplImage *mframe,*current,*frg,*test; int *fg,*bg_bw,*rank_ind; double *w,*mean,*sd,*u_diff,*rank; int C,M,sd_init,i,j,k,m,rand_temp=0,rank_ind_temp=0,min_index=0,x=0,y=0,counter_frame=0; double D,alph,thresh,p,temp; CvRNG state; int match,height,width; mframe=cvQueryFrame(capture); frg = cvCreateImage(cvSize(mframe->width,mframe->height),IPL_DEPTH_8U,1); current = cvCreateImage(cvSize(mframe->width,mframe->height),IPL_DEPTH_8U,1); test = cvCreateImage(cvSize(mframe->width,mframe->height),IPL_DEPTH_8U,1); C = 4; //number of gaussian components (typically 3-5) M = 4; //number of background components sd_init = 6; //initial standard deviation (for new components) var = 36 in paper alph = 0.01; //learning rate (between 0 and 1) (from paper 0.01) D = 2.5; //positive deviation threshold thresh = 0.25; //foreground threshold (0.25 or 0.75 in paper) p = alph/(1/C); //initial p variable (used to update mean and sd) height=current->height;width=current->widthStep; fg = (int *)malloc(sizeof(int)*width*height); //foreground array bg_bw = (int *)malloc(sizeof(int)*width*height); //background array rank = (double *)malloc(sizeof(double)*1*C); //rank of components (w/sd) w = (double *)malloc(sizeof(double)*width*height*C); //weights array mean = (double *)malloc(sizeof(double)*width*height*C); //pixel means sd = (double *)malloc(sizeof(double)*width*height*C); //pixel standard deviations u_diff = (double *)malloc(sizeof(double)*width*height*C); //difference of each pixel from mean for (i=0;iimageData[i*width+j]-mean[i*width*C+j*C+m]); } } } //update gaussian components for each pixel for (i=0;iimageData[i*width+j]; sd[i*width*C+j*C+k] =sqrt((1-p)*(sd[i*width*C+j*C+k]*sd[i*width*C+j*C+k]) + p*(pow((uchar)current->imageData[i*width+j] - mean[i*width*C+j*C+k],2))); }else{ w[i*width*C+j*C+k] = (1-alph)*w[i*width*C+j*C+k]; // weight slighly decreases } temp += w[i*width*C+j*C+k]; } for(k=0;kimageData[i*width+j] = (uchar)bg_bw[i*width+j]; //if no components match, create new component if (match == 0) { mean[i*width*C+j*C+min_index] = (uchar)current->imageData[i*width+j]; //printf("%d ",(uchar)bg->imageData[i*width+j]); sd[i*width*C+j*C+min_index] = sd_init; } for (k=0;k rank[m]) { //swap max values rand_temp = rank[m]; rank[m] = rank[k]; rank[k] = rand_temp; //swap max index values rank_ind_temp = rank_ind[m]; rank_ind[m] = rank_ind[k]; rank_ind[k] = rank_ind_temp; } } } //calculate foreground match = 0;k = 0; //frg->imageData[i*width+j]=0; while ((match == 0)&&(k= thresh) if (abs(u_diff[i*width*C+j*C+rank_ind[k]]) <= D*sd[i*width*C+j*C+rank_ind[k]]){ frg->imageData[i*width+j] = 0; match = 1; } else frg->imageData[i*width+j] = (uchar)current->imageData[i*width+j]; k = k+1; } } } mframe = cvQueryFrame(capture); cvShowImage("fore",frg); cvShowImage("back",test); char s=cvWaitKey(33); if(s==27) break; free(rank_ind); } free(fg);free(w);free(mean);free(sd);free(u_diff);free(rank); cvNamedWindow("back",0); cvNamedWindow("fore",0); cvReleaseCapture(&capture); cvDestroyWindow("fore"); cvDestroyWindow("back"); return 0; }