四.中国剩余定理 ( 孙子定理 / CRT )
1.描述:
设正整数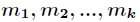 两两互素,则同余方程组
两两互素,则同余方程组
 有整数解。并且在模
有整数解。并且在模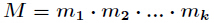 下的解是唯一的,解为
下的解是唯一的,解为
 其中
其中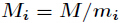 ,而
,而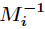 为
为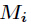 模
模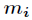 的逆元。
的逆元。
2.代码实现:
(1)互质://求M%A=a,M%B=b,...中的M,其中A,B,C...互质
int CRT(int a[],int m[],int n){
int M = 1;
int ans = 0;
for(int i=1; i<=n; i++)
M *= m[i];
for(int i=1; i<=n; i++){
int x, y;
int Mi = M / m[i];
ex_gcd(Mi, m[i], x, y);
ans = (ans + Mi * x * a[i]) % M;
}
if(ans < 0)
ans += M;
return ans;
}
(2)非互质:
一般的中国剩余定理要求mi两两互质,但是保证互质条件太苛刻了,若mi并不满足两两互质时,就要采用两两合并的思想,假设要合并如下两个方程 x=a1+m1*x1
x=a2+m2*x2 得到
a1+m1*x1 = a2+m2*x2 → m1*x1+m2*x2 = a2-a1 再通过扩展欧几里得算法解出x1的最小正整数解,代入
x=a1+m1*x1 得到x后合并为一个方程的结果为
y ≡ x(mod lcm(m1,m2)) 这样一直合并下去,最终可以求得同余方程组的解。 代码:
bool merge(LL a1, LL m1, LL a2, LL m2, LL &a3, LL &m3) {
LL d = gcd(m1, m2);
LL c = a2 - a1;
if(c % d) return false;
c = (c % m2 + m2) % m2;
m1 /= d;
m2 /= d;
c /= d;
c *= Inv(m1, m2);//Inv为乘法逆元,数论常用内容——欧几里得算法与扩展欧几里得算法
c %= m2;
c *= m1 * d;
c += a1;
m3 = m1 * m2 * d;
a3 = (c % m3 + m3) % m3;
return true;
}
LL CRT(LL a[], LL m[], int n) {
LL a1 = a[1];
LL m1 = m[1];
for(int i=2; i<=n; i++) {
LL a2 = a[i];
LL m2 = m[i];
LL m3, a3;
if(!merge(a1, m1, a2, m2, a3, m3))
return -1;
a1 = a3;
m1 = m3;
}
return (a1 % m1 + m1) % m1;
}
3.例题:
(1) POJ 1006 题意: 人自出生起就有体力,情感和智力三个生理周期,分别为23,28和33天。一个周期内有一天为峰值,在这一天,人在对应的方面(体力,情感或智力)表现最好。通常这三个周期的峰值不会是同一天。现在给出三个日期,分别对应于体力,情感,智力出现峰值的日期。然后再给出一个起始日期,要求从这一天开始,算出最少再过多少天后三个峰值同时出现。 代码:#include
#include
#include
#include
#include
#include
#include
#include
#include
#include
#include
using namespace std;
#define eps 1e-10
#define INF 0x3f3f3f3f
typedef long long LL;
void ex_gcd(LL a, LL b, LL &x, LL &y, LL &d)
{
if (!b)
{
d = a, x = 1, y = 0;
}
else
{
ex_gcd(b, a % b, y, x, d);
y -= x * (a / b);
}
}
LL inv(LL a,LL b)
{
LL d, x, y;
ex_gcd(a, b, x, y, d);
return d == 1 ? (x % b + b) % b : -1;
}
LL CRT(LL *t,LL *m,int n)
{
LL M=1,ans=0;
for(int i=0; i>t[0]>>t[1]>>t[2]>>z&&(~t[0]||~t[1]||~t[2]||~z))
{
LL days;
cout<<"Case 1: the next triple peak occurs in ";
days=(CRT(t,m,3)-z+MOD)%MOD;
if(!days)
days+=MOD;
cout<