由相同的玻 {MOD}子系集组成的力学系统等效于由一组振子组成的力学系统---这两个系统恰恰是从两种不同观点来看待的同一个系统,每一个独立的玻 {MOD}子态伴随着一个振子.这里我们有了量子力学最基本的结果果之一,它使光的波动理论与微粒理论的统一得以实现。
所以如果模拟了振子系统也就相当于模拟了玻 {MOD}子系统,也就是模拟了波粒二象性。
假设神经网络的作用相当于振子动力系统,那么被分类对象就是振子,神经网络就构成一个弹簧,所以神经网络就可以用下面的公式表达
 下面就做实验验证是否有可能,
下面就做实验验证是否有可能,
 如图中C所示,物体ma和mb相当于被分类对象,假如被分类对象minst0是ma,minst5是mb,则图C可以得出方程
如图中C所示,物体ma和mb相当于被分类对象,假如被分类对象minst0是ma,minst5是mb,则图C可以得出方程
 而图C和图D是等价的
而图C和图D是等价的
 再假设两个网络E和F引入第三方参照物X,在E中让minst0和X分类,在F中让minst5和x分类。
则有方程
再假设两个网络E和F引入第三方参照物X,在E中让minst0和X分类,在F中让minst5和x分类。
则有方程

 现在让这个网络的结构是有1个3*3的卷积核,49*30*2的节点数,将minst的图片缩小到9*9,这个网络简写作
d2(minst0,5)81-con(3*3)49-30-2-(2*k) ,k∈(0,1)
意思是用带有一个3*3卷积核,结构是49*30*2的网络让0向1,0收敛;让5向0,1收敛,二分类minst0,5的网络。
ω05的具体测量过程是
具体进样顺序
δ=0.1
初始化权重
迭代次数
minst 0-1
1
判断是否达到收敛
minst 5-1
2
判断是否达到收敛
梯度下降
minst 0-2
3
判断是否达到收敛
minst 5-2
4
判断是否达到收敛
梯度下降
……
minst 0-4999
9997
判断是否达到收敛
minst 5-4999
9998
判断是否达到收敛
梯度下降
……
如果4999图片内没有达到收敛标准再次从头循环
minst 0-1
9999
判断是否达到收敛
minst 5-1
10000
判断是否达到收敛
梯度下降
……
每当网路达到收敛标准记录迭代次数和对应的准确率测试结果
将这一过程重复199次
δ=0.01
…
δ=1e-7
收敛条件是
if (Math.abs(f2[0]-y[0])< δ && Math.abs(f2[1]-y[1])< δ )
根据前面大量的实验任何一个网络对应一个δ都有一个特征的迭代次数n,与之对应的就有一条n(δ)曲线,让n等于公式里的ω
用同样的办法做另外的两个网络
d2(minstx,0)81-con(3*3)49-30-2-(2*k) ,k∈(0,1)
意思是用同样的网络分类minst的0和一张x图片,让0向1,0收敛,让x向0,1收敛
d2(minstx,5)81-con(3*3)49-30-2-(2*k) ,k∈(0,1)
意思是用同样的网络分类minst的5和一张x图片,让x向1,0收敛,让5向0,1收敛
现在让这个网络的结构是有1个3*3的卷积核,49*30*2的节点数,将minst的图片缩小到9*9,这个网络简写作
d2(minst0,5)81-con(3*3)49-30-2-(2*k) ,k∈(0,1)
意思是用带有一个3*3卷积核,结构是49*30*2的网络让0向1,0收敛;让5向0,1收敛,二分类minst0,5的网络。
ω05的具体测量过程是
具体进样顺序
δ=0.1
初始化权重
迭代次数
minst 0-1
1
判断是否达到收敛
minst 5-1
2
判断是否达到收敛
梯度下降
minst 0-2
3
判断是否达到收敛
minst 5-2
4
判断是否达到收敛
梯度下降
……
minst 0-4999
9997
判断是否达到收敛
minst 5-4999
9998
判断是否达到收敛
梯度下降
……
如果4999图片内没有达到收敛标准再次从头循环
minst 0-1
9999
判断是否达到收敛
minst 5-1
10000
判断是否达到收敛
梯度下降
……
每当网路达到收敛标准记录迭代次数和对应的准确率测试结果
将这一过程重复199次
δ=0.01
…
δ=1e-7
收敛条件是
if (Math.abs(f2[0]-y[0])< δ && Math.abs(f2[1]-y[1])< δ )
根据前面大量的实验任何一个网络对应一个δ都有一个特征的迭代次数n,与之对应的就有一条n(δ)曲线,让n等于公式里的ω
用同样的办法做另外的两个网络
d2(minstx,0)81-con(3*3)49-30-2-(2*k) ,k∈(0,1)
意思是用同样的网络分类minst的0和一张x图片,让0向1,0收敛,让x向0,1收敛
d2(minstx,5)81-con(3*3)49-30-2-(2*k) ,k∈(0,1)
意思是用同样的网络分类minst的5和一张x图片,让x向1,0收敛,让5向0,1收敛
 相当于让三个对象两两分类,让各自成为另外两个的参照物。
ω05,ωx0,ωx5都可以通过实验测出来,k可以约掉。所以ω0,ω5,ωx都可以计算出来,具体数据
δ
实测ω05
实测ωx0
实测ωx5
计算ωx
计算ω0
计算ω5
0.1
3508.41206
2472.38693
3323.90955
2405.18568
2545.55529
11070.994
0.01
4482.32161
3167.76382
4332.09045
3113.37833
3225.10272
17139.5484
0.001
6103.9397
4400.33668
5487.79899
4151.90956
4699.45802
10911.0006
1.00E-04
8919.69849
6164.71859
7451.38693
5611.71821
6921.8395
15310.0051
9.00E-05
9349.0201
6342.79899
7405.58794
5621.06102
7440.43971
14405.7759
8.00E-05
9539.44221
6398.79899
7552.99497
5682.96375
7477.91464
15627.1984
7.00E-05
10203.4322
6637.88442
7724.74372
5788.11728
8021.23091
16511.343
6.00E-05
9851.55276
6804.88945
7680.52261
5950.32629
8179.43801
13291.6796
5.00E-05
10868.8342
7217
8680.79397
6454.36378
8335.01776
19857.1576
4.00E-05
11182.1005
7507.39196
8660.1608
6582.52029
8977.85924
16693.7807
3.00E-05
12931.1709
7946.28643
9033.28643
6724.97923
10226.2497
20419.9466
2.00E-05
14625.3216
8857.38191
10089.8794
7475.60284
11471.6203
23895.9251
1.00E-05
20225.7739
10095.7136
11588.8643
8216.42308
14418.9448
112416.706
9.00E-06
21326.7688
10820.3769
11692.2714
8556.92031
17087.2773
32070.2844
8.00E-06
23468.9447
10830.608
12298.2613
8664.223
16376.1186
#NUM!
7.00E-06
24229.2161
11451.1809
12493.6382
9006.03169
18496.5046
45459.6581
6.00E-06
27358.9749
11989.7337
12861.1256
9258.46656
21097.3907
48491.3931
5.00E-06
31394.1859
12050.6683
13186.9146
9275.91094
21565.6545
#NUM!
4.00E-06
36071.5075
13025.0905
15299.7286
10315.3927
20451.1335
#NUM!
3.00E-06
43770.6281
14325.3719
15631.196
10882.6205
27712.5188
#NUM!
2.00E-06
53362.9598
15382.9698
17096.2412
11707.2494
29415.371
#NUM!
1.00E-06
76472.8291
19339.2412
21160.8241
14530.965
40438.7682
#NUM!
9.00E-07
86231.8492
20197.5528
20843.5578
14714.4894
59331.1441
#NUM!
8.00E-07
91895.4472
19328.6583
20997.8492
14394.3721
43558.2461
#NUM!
7.00E-07
94373.5528
21669.5729
21982.2714
15642.6219
76152.8888
138511.699
6.00E-07
101428.583
23628.8191
24435.0251
17229.2827
68447.7713
#NUM!
5.00E-07
95963.7688
24159.4422
24493.1256
17483.1843
80334.2167
126770.12
4.00E-07
112533.327
24202.1357
27362.5528
18368.2731
47110.8355
#NUM!
3.00E-07
120549.251
30488.2161
30380.2714
21871.4863
127875.017
114353.599
2.00E-07
135646.754
35339.0101
32491.4573
24299.0927
#NUM!
70560.5981
1.00E-07
159863.347
41935.7035
43337.4673
30686.5925
115224.791
583311.258
比较计算出来的ω0,ω5的曲线
相当于让三个对象两两分类,让各自成为另外两个的参照物。
ω05,ωx0,ωx5都可以通过实验测出来,k可以约掉。所以ω0,ω5,ωx都可以计算出来,具体数据
δ
实测ω05
实测ωx0
实测ωx5
计算ωx
计算ω0
计算ω5
0.1
3508.41206
2472.38693
3323.90955
2405.18568
2545.55529
11070.994
0.01
4482.32161
3167.76382
4332.09045
3113.37833
3225.10272
17139.5484
0.001
6103.9397
4400.33668
5487.79899
4151.90956
4699.45802
10911.0006
1.00E-04
8919.69849
6164.71859
7451.38693
5611.71821
6921.8395
15310.0051
9.00E-05
9349.0201
6342.79899
7405.58794
5621.06102
7440.43971
14405.7759
8.00E-05
9539.44221
6398.79899
7552.99497
5682.96375
7477.91464
15627.1984
7.00E-05
10203.4322
6637.88442
7724.74372
5788.11728
8021.23091
16511.343
6.00E-05
9851.55276
6804.88945
7680.52261
5950.32629
8179.43801
13291.6796
5.00E-05
10868.8342
7217
8680.79397
6454.36378
8335.01776
19857.1576
4.00E-05
11182.1005
7507.39196
8660.1608
6582.52029
8977.85924
16693.7807
3.00E-05
12931.1709
7946.28643
9033.28643
6724.97923
10226.2497
20419.9466
2.00E-05
14625.3216
8857.38191
10089.8794
7475.60284
11471.6203
23895.9251
1.00E-05
20225.7739
10095.7136
11588.8643
8216.42308
14418.9448
112416.706
9.00E-06
21326.7688
10820.3769
11692.2714
8556.92031
17087.2773
32070.2844
8.00E-06
23468.9447
10830.608
12298.2613
8664.223
16376.1186
#NUM!
7.00E-06
24229.2161
11451.1809
12493.6382
9006.03169
18496.5046
45459.6581
6.00E-06
27358.9749
11989.7337
12861.1256
9258.46656
21097.3907
48491.3931
5.00E-06
31394.1859
12050.6683
13186.9146
9275.91094
21565.6545
#NUM!
4.00E-06
36071.5075
13025.0905
15299.7286
10315.3927
20451.1335
#NUM!
3.00E-06
43770.6281
14325.3719
15631.196
10882.6205
27712.5188
#NUM!
2.00E-06
53362.9598
15382.9698
17096.2412
11707.2494
29415.371
#NUM!
1.00E-06
76472.8291
19339.2412
21160.8241
14530.965
40438.7682
#NUM!
9.00E-07
86231.8492
20197.5528
20843.5578
14714.4894
59331.1441
#NUM!
8.00E-07
91895.4472
19328.6583
20997.8492
14394.3721
43558.2461
#NUM!
7.00E-07
94373.5528
21669.5729
21982.2714
15642.6219
76152.8888
138511.699
6.00E-07
101428.583
23628.8191
24435.0251
17229.2827
68447.7713
#NUM!
5.00E-07
95963.7688
24159.4422
24493.1256
17483.1843
80334.2167
126770.12
4.00E-07
112533.327
24202.1357
27362.5528
18368.2731
47110.8355
#NUM!
3.00E-07
120549.251
30488.2161
30380.2714
21871.4863
127875.017
114353.599
2.00E-07
135646.754
35339.0101
32491.4573
24299.0927
#NUM!
70560.5981
1.00E-07
159863.347
41935.7035
43337.4673
30686.5925
115224.791
583311.258
比较计算出来的ω0,ω5的曲线
 这两条曲线是明显分开的,所以可以将它们分类,也表明神经网络的迭代次数是由参与分类的对象的特征频率合成的。
所以网络d2(minst0,5)81-con(3*3)49-30-2-(2*k) ,k∈(0,1)
的迭代次数n的精确表达式为
这两条曲线是明显分开的,所以可以将它们分类,也表明神经网络的迭代次数是由参与分类的对象的特征频率合成的。
所以网络d2(minst0,5)81-con(3*3)49-30-2-(2*k) ,k∈(0,1)
的迭代次数n的精确表达式为
 质量m0,m5,mx0,mx5,m05也可以计算出来
δ
mx
m0
m5
mxo
mx5
m05
0.1
1
0.892755
0.047198
1.892755
1.047198
0.939953
0.01
1
0.931916
0.032996
1.931916
1.032996
0.964912
0.001
1
0.780549
0.144799
1.780549
1.144799
0.925348
1.00E-04
1
0.657277
0.134351
1.657277
1.134351
0.791628
9.00E-05
1
0.570741
0.152252
1.570741
1.152252
0.722994
8.00E-05
1
0.577549
0.132248
1.577549
1.132248
0.709796
7.00E-05
1
0.520706
0.122888
1.520706
1.122888
0.643594
6.00E-05
1
0.529218
0.200411
1.529218
1.200411
0.729629
5.00E-05
1
0.599644
0.105651
1.599644
1.105651
0.705295
4.00E-05
1
0.537575
0.15548
1.537575
1.15548
0.693055
3.00E-05
1
0.432463
0.108461
1.432463
1.108461
0.540924
2.00E-05
1
0.424662
0.097869
1.424662
1.097869
0.52253
1.00E-05
1
0.324712
0.005342
1.324712
1.005342
0.330054
9.00E-06
1
0.250778
0.071192
1.250778
1.071192
0.32197
8.00E-06
1
0.279922
#NUM!
1.279922
#NUM!
#NUM!
7.00E-06
1
0.237076
0.039248
1.237076
1.039248
0.276324
6.00E-06
1
0.192584
0.036454
1.192584
1.036454
0.229038
5.00E-06
1
0.185007
#NUM!
1.185007
#NUM!
#NUM!
4.00E-06
1
0.254412
#NUM!
1.254412
#NUM!
#NUM!
3.00E-06
1
0.154211
#NUM!
1.154211
#NUM!
#NUM!
2.00E-06
1
0.158402
#NUM!
1.158402
#NUM!
#NUM!
1.00E-06
1
0.12912
#NUM!
1.12912
#NUM!
#NUM!
9.00E-07
1
0.061507
#NUM!
1.061507
#NUM!
#NUM!
8.00E-07
1
0.109206
#NUM!
1.109206
#NUM!
#NUM!
7.00E-07
1
0.042194
0.012754
1.042194
1.012754
0.054948
6.00E-07
1
0.06336
#NUM!
1.06336
#NUM!
#NUM!
5.00E-07
1
0.047363
0.01902
1.047363
1.01902
0.066383
4.00E-07
1
0.152018
#NUM!
1.152018
#NUM!
#NUM!
3.00E-07
1
0.029254
0.036581
1.029254
1.036581
0.065835
2.00E-07
1
#NUM!
0.118592
#NUM!
1.118592
#NUM!
1.00E-07
1
0.070926
0.002768
1.070926
1.002768
0.073694
质量m0,m5,mx0,mx5,m05也可以计算出来
δ
mx
m0
m5
mxo
mx5
m05
0.1
1
0.892755
0.047198
1.892755
1.047198
0.939953
0.01
1
0.931916
0.032996
1.931916
1.032996
0.964912
0.001
1
0.780549
0.144799
1.780549
1.144799
0.925348
1.00E-04
1
0.657277
0.134351
1.657277
1.134351
0.791628
9.00E-05
1
0.570741
0.152252
1.570741
1.152252
0.722994
8.00E-05
1
0.577549
0.132248
1.577549
1.132248
0.709796
7.00E-05
1
0.520706
0.122888
1.520706
1.122888
0.643594
6.00E-05
1
0.529218
0.200411
1.529218
1.200411
0.729629
5.00E-05
1
0.599644
0.105651
1.599644
1.105651
0.705295
4.00E-05
1
0.537575
0.15548
1.537575
1.15548
0.693055
3.00E-05
1
0.432463
0.108461
1.432463
1.108461
0.540924
2.00E-05
1
0.424662
0.097869
1.424662
1.097869
0.52253
1.00E-05
1
0.324712
0.005342
1.324712
1.005342
0.330054
9.00E-06
1
0.250778
0.071192
1.250778
1.071192
0.32197
8.00E-06
1
0.279922
#NUM!
1.279922
#NUM!
#NUM!
7.00E-06
1
0.237076
0.039248
1.237076
1.039248
0.276324
6.00E-06
1
0.192584
0.036454
1.192584
1.036454
0.229038
5.00E-06
1
0.185007
#NUM!
1.185007
#NUM!
#NUM!
4.00E-06
1
0.254412
#NUM!
1.254412
#NUM!
#NUM!
3.00E-06
1
0.154211
#NUM!
1.154211
#NUM!
#NUM!
2.00E-06
1
0.158402
#NUM!
1.158402
#NUM!
#NUM!
1.00E-06
1
0.12912
#NUM!
1.12912
#NUM!
#NUM!
9.00E-07
1
0.061507
#NUM!
1.061507
#NUM!
#NUM!
8.00E-07
1
0.109206
#NUM!
1.109206
#NUM!
#NUM!
7.00E-07
1
0.042194
0.012754
1.042194
1.012754
0.054948
6.00E-07
1
0.06336
#NUM!
1.06336
#NUM!
#NUM!
5.00E-07
1
0.047363
0.01902
1.047363
1.01902
0.066383
4.00E-07
1
0.152018
#NUM!
1.152018
#NUM!
#NUM!
3.00E-07
1
0.029254
0.036581
1.029254
1.036581
0.065835
2.00E-07
1
#NUM!
0.118592
#NUM!
1.118592
#NUM!
1.00E-07
1
0.070926
0.002768
1.070926
1.002768
0.073694
 minst0和minst5的质量m0和m5也是分开的。
如果让mx恒为1,则当δ=0.1时,图片集0的质量是0.892755,图片集5的质量是0.047198。
所以将神经网络理解成是一个振子动力系统在数学上是可能的,那这个系统与波粒二象性有什么关系?
minst0和minst5的质量m0和m5也是分开的。
如果让mx恒为1,则当δ=0.1时,图片集0的质量是0.892755,图片集5的质量是0.047198。
所以将神经网络理解成是一个振子动力系统在数学上是可能的,那这个系统与波粒二象性有什么关系?
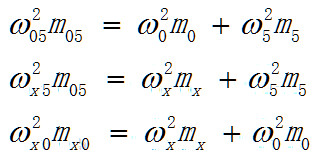 比如看这 3个方程,可以猜测如果3个被分类对象中少了任何一个,则方程仅剩下一个比如
比如看这 3个方程,可以猜测如果3个被分类对象中少了任何一个,则方程仅剩下一个比如
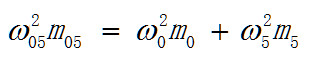 对应这个方程的解这6个未知数可能属于全体实数集,
对应这个方程的解这6个未知数可能属于全体实数集,
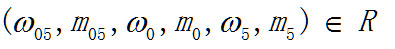 这种状态就像波,分布在整个空间又几乎不在任何地方。
而当加入第三个分类对象的时候,网络构成了方程组,解就变成唯一的,同时具有了确定的质量,如果将第三个分类对象理解成是测量行为本身,则可以解释成是测量行为使波坍缩到一点,由波变成了粒子。
实验数据
学习率 0.1
权重初始化方式
Random rand1 =new Random();
int ti1=rand1.nextInt(98)+1;
int xx=1;
if(ti1%2==0)
{ xx=-1;}
tw[a][b]=xx*((double)ti1/x);
第一层第二层和卷积核的权重的初始化的x分别为1000,1000,200
d2(minst0,5)81-con(3*3)49-30-2-(2*k) ,k∈(0,1)
的数据在《共振耦合二分类0,5神经网络迭代次数和准确率估算表达式》2019-1-24已经给出了
d2(minstx,0)81-con(3*3)49-30-2-(2*k) ,k∈(0,1)的数据已经在《神经网络与并联的弹簧》2019-2-2中给出了
d2(minstx,5)81-con(3*3)49-30-2-(2*k) ,k∈(0,1)的数据
x5
f2[0]
f2[1]
迭代次数n
平均准确率p-ave
δ
耗时ms/次
耗时ms/199次
耗时 min/199
最大准确率p-max
0.500523
0.500821271
18.0201005
0.5044614
0.5
619.0050251
123182
2.053033
0.71741453
0.389638
0.610526296
2313.20603
0.5242774
0.4
992.879397
197598
3.2933
0.790598291
0.284278
0.715427717
2694.241206
0.5197784
0.3
1057.954774
210533
3.508883
0.766025641
0.180895
0.819382042
2796.231156
0.515521
0.2
1072.899497
213507
3.55845
0.770299145
0.083688
0.916218803
3323.909548
0.5206696
0.1
1159.316583
230704
3.845067
0.773504274
0.00744
0.992577781
4332.090452
0.5062036
0.01
1493.884422
297283
4.954717
0.785790598
7.30E-04
0.999270412
5487.798995
0.5115589
0.001
2001.663317
398331
6.63885
0.713675214
6.50E-05
0.999934855
7451.386935
0.5039433
1.00E-04
2400.668342
477749
7.962483
0.682692308
5.82E-05
0.999941752
7405.58794
0.5015328
9.00E-05
2409.105528
479412
7.9902
0.641559829
5.27E-05
0.999947399
7552.994975
0.5055888
8.00E-05
2429.100503
483407
8.056783
0.650641026
4.65E-05
0.999953413
7724.743719
0.4991705
7.00E-05
2117.396985
421378
7.022967
0.69017094
3.97E-05
0.999960261
7680.522613
0.5014522
6.00E-05
2427.552764
483083
8.051383
0.691773504
3.30E-05
0.999967048
8680.79397
0.5036642
5.00E-05
2628.030151
522994
8.716567
0.744123932
2.63E-05
0.99997375
8660.160804
0.505511
4.00E-05
2634.20603
524207
8.736783
0.780448718
1.98E-05
0.999980146
9033.286432
0.5046117
3.00E-05
2719.296482
541140
9.019
0.634615385
1.31E-05
0.999986908
10089.8794
0.5041232
2.00E-05
2933.361809
583739
9.728983
0.719017094
6.67E-06
0.999993342
11588.86432
0.5008858
1.00E-05
3240.175879
644825
10.74708
0.594551282
6.21E-06
0.999993796
11692.27136
0.4990551
9.00E-06
3260.477387
648835
10.81392
0.789529915
5.28E-06
0.999994727
12298.26131
0.504295
8.00E-06
3380.964824
672812
11.21353
0.670405983
4.89E-06
0.99999511
12493.63819
0.5036454
7.00E-06
3455.201005
687590
11.45983
0.708867521
3.88E-06
0.999996116
12861.12563
0.503342
6.00E-06
3503.849246
697273
11.62122
0.680555556
3.40E-06
0.999996605
13186.91457
0.5014281
5.00E-06
3572.115578
710854
11.84757
0.68482906
2.74E-06
0.999997256
15299.72864
0.4974767
4.00E-06
3695.798995
735471
12.25785
0.706196581
1.95E-06
0.999998048
15631.19598
0.50142
3.00E-06
4089.135678
813743
13.56238
0.662393162
1.35E-06
0.999998647
17096.24121
0.5003302
2.00E-06
4386.512563
872921
14.54868
0.723290598
7.07E-07
0.999999294
21160.82412
0.4904974
1.00E-06
5203.472362
1035525
17.25875
0.65758547
6.14E-07
0.999999386
20843.55779
0.5033447
9.00E-07
5137.778894
1022418
17.0403
0.704059829
5.49E-07
0.99999945
20997.84925
0.4993772
8.00E-07
5154.949749
1025835
17.09725
0.677350427
4.79E-07
0.999999521
21982.27136
0.5002819
7.00E-07
5355.653266
1065806
17.76343
0.64957265
4.19E-07
0.999999581
24435.02513
0.4953077
6.00E-07
5869.919598
1168114
19.46857
0.652777778
3.40E-07
0.99999966
24493.12563
0.4882935
5.00E-07
5871.81407
1168491
19.47485
0.638354701
2.72E-07
0.999999727
27362.55276
0.4927979
4.00E-07
6503.80402
1294263
21.57105
0.647970085
2.13E-07
0.999999787
30380.27136
0.4942689
3.00E-07
6695.165829
1332342
22.2057
0.647970085
1.43E-07
0.999999857
32491.45729
0.4974042
2.00E-07
7507.125628
1493922
24.8987
0.698183761
7.16E-08
0.999999928
43337.46734
0.4909752
1.00E-07
9691.366834
1928589
32.14315
0.667200855
f2[0] f2[1] 迭代次数n 平均准确率p-ave δ 耗时ms/次
这种状态就像波,分布在整个空间又几乎不在任何地方。
而当加入第三个分类对象的时候,网络构成了方程组,解就变成唯一的,同时具有了确定的质量,如果将第三个分类对象理解成是测量行为本身,则可以解释成是测量行为使波坍缩到一点,由波变成了粒子。
实验数据
学习率 0.1
权重初始化方式
Random rand1 =new Random();
int ti1=rand1.nextInt(98)+1;
int xx=1;
if(ti1%2==0)
{ xx=-1;}
tw[a][b]=xx*((double)ti1/x);
第一层第二层和卷积核的权重的初始化的x分别为1000,1000,200
d2(minst0,5)81-con(3*3)49-30-2-(2*k) ,k∈(0,1)
的数据在《共振耦合二分类0,5神经网络迭代次数和准确率估算表达式》2019-1-24已经给出了
d2(minstx,0)81-con(3*3)49-30-2-(2*k) ,k∈(0,1)的数据已经在《神经网络与并联的弹簧》2019-2-2中给出了
d2(minstx,5)81-con(3*3)49-30-2-(2*k) ,k∈(0,1)的数据
x5
f2[0]
f2[1]
迭代次数n
平均准确率p-ave
δ
耗时ms/次
耗时ms/199次
耗时 min/199
最大准确率p-max
0.500523
0.500821271
18.0201005
0.5044614
0.5
619.0050251
123182
2.053033
0.71741453
0.389638
0.610526296
2313.20603
0.5242774
0.4
992.879397
197598
3.2933
0.790598291
0.284278
0.715427717
2694.241206
0.5197784
0.3
1057.954774
210533
3.508883
0.766025641
0.180895
0.819382042
2796.231156
0.515521
0.2
1072.899497
213507
3.55845
0.770299145
0.083688
0.916218803
3323.909548
0.5206696
0.1
1159.316583
230704
3.845067
0.773504274
0.00744
0.992577781
4332.090452
0.5062036
0.01
1493.884422
297283
4.954717
0.785790598
7.30E-04
0.999270412
5487.798995
0.5115589
0.001
2001.663317
398331
6.63885
0.713675214
6.50E-05
0.999934855
7451.386935
0.5039433
1.00E-04
2400.668342
477749
7.962483
0.682692308
5.82E-05
0.999941752
7405.58794
0.5015328
9.00E-05
2409.105528
479412
7.9902
0.641559829
5.27E-05
0.999947399
7552.994975
0.5055888
8.00E-05
2429.100503
483407
8.056783
0.650641026
4.65E-05
0.999953413
7724.743719
0.4991705
7.00E-05
2117.396985
421378
7.022967
0.69017094
3.97E-05
0.999960261
7680.522613
0.5014522
6.00E-05
2427.552764
483083
8.051383
0.691773504
3.30E-05
0.999967048
8680.79397
0.5036642
5.00E-05
2628.030151
522994
8.716567
0.744123932
2.63E-05
0.99997375
8660.160804
0.505511
4.00E-05
2634.20603
524207
8.736783
0.780448718
1.98E-05
0.999980146
9033.286432
0.5046117
3.00E-05
2719.296482
541140
9.019
0.634615385
1.31E-05
0.999986908
10089.8794
0.5041232
2.00E-05
2933.361809
583739
9.728983
0.719017094
6.67E-06
0.999993342
11588.86432
0.5008858
1.00E-05
3240.175879
644825
10.74708
0.594551282
6.21E-06
0.999993796
11692.27136
0.4990551
9.00E-06
3260.477387
648835
10.81392
0.789529915
5.28E-06
0.999994727
12298.26131
0.504295
8.00E-06
3380.964824
672812
11.21353
0.670405983
4.89E-06
0.99999511
12493.63819
0.5036454
7.00E-06
3455.201005
687590
11.45983
0.708867521
3.88E-06
0.999996116
12861.12563
0.503342
6.00E-06
3503.849246
697273
11.62122
0.680555556
3.40E-06
0.999996605
13186.91457
0.5014281
5.00E-06
3572.115578
710854
11.84757
0.68482906
2.74E-06
0.999997256
15299.72864
0.4974767
4.00E-06
3695.798995
735471
12.25785
0.706196581
1.95E-06
0.999998048
15631.19598
0.50142
3.00E-06
4089.135678
813743
13.56238
0.662393162
1.35E-06
0.999998647
17096.24121
0.5003302
2.00E-06
4386.512563
872921
14.54868
0.723290598
7.07E-07
0.999999294
21160.82412
0.4904974
1.00E-06
5203.472362
1035525
17.25875
0.65758547
6.14E-07
0.999999386
20843.55779
0.5033447
9.00E-07
5137.778894
1022418
17.0403
0.704059829
5.49E-07
0.99999945
20997.84925
0.4993772
8.00E-07
5154.949749
1025835
17.09725
0.677350427
4.79E-07
0.999999521
21982.27136
0.5002819
7.00E-07
5355.653266
1065806
17.76343
0.64957265
4.19E-07
0.999999581
24435.02513
0.4953077
6.00E-07
5869.919598
1168114
19.46857
0.652777778
3.40E-07
0.99999966
24493.12563
0.4882935
5.00E-07
5871.81407
1168491
19.47485
0.638354701
2.72E-07
0.999999727
27362.55276
0.4927979
4.00E-07
6503.80402
1294263
21.57105
0.647970085
2.13E-07
0.999999787
30380.27136
0.4942689
3.00E-07
6695.165829
1332342
22.2057
0.647970085
1.43E-07
0.999999857
32491.45729
0.4974042
2.00E-07
7507.125628
1493922
24.8987
0.698183761
7.16E-08
0.999999928
43337.46734
0.4909752
1.00E-07
9691.366834
1928589
32.14315
0.667200855
f2[0] f2[1] 迭代次数n 平均准确率p-ave δ 耗时ms/次
0.468200365 0.530903512 2 0.476495726 0.5 1423
0.498897295 0.500553235 32 0.540064103 0.5 736
0.497988522 0.500266399 40 0.472222222 0.5 704
0.437232597 0.505406109 2 0.476495726 0.5 673
0.499074493 0.50005661 38 0.450320513 0.5 658
0.491607777 0.539615398 2 0.476495726 0.5 641
0.49966528 0.500178772 34 0.563034188 0.5 657
0.498825797 0.500267978 36 0.465277778 0.5 660
0.499586943 0.579232755 2 0.476495726 0.5 609
0.499805306 0.500262273 50 0.542735043 0.5 627
0.550587527 0.492391858 1 0.523504274 0.5 610
0.494475659 0.53181447 2 0.476495726 0.5 626
0.499455292 0.501160016 42 0.408119658 0.5 642
0.499991638 0.501293813 42 0.438034188 0.5 626
0.501193324 0.499913881 21 0.523504274 0.5 610
0.500000563 0.498896864 31 0.523504274 0.5 627
0.498638626 0.501204415 42 0.503205128 0.5 610
0.499627355 0.500968078 42 0.509081197 0.5 615
0.499972285 0.500301157 46 0.409188034 0.5 626
0.478716818 0.562916511 2 0.476495726 0.5 626
0.46637963 0.514216773 2 0.476495726 0.5 610
0.528095228 0.462601235 1 0.523504274 0.5 595
0.552414594 0.462272422 1 0.523504274 0.5 616
0.484999193 0.565478321 2 0.476495726 0.5 596
0.561031885 0.446968998 1 0.523504274 0.5 625
0.498917913 0.500439205 48 0.458867521 0.5 627
0.50186706 0.499933549 45 0.523504274 0.5 610
0.490942119 0.500232783 20 0.476495726 0.5 643
0.499706075 0.500601114 50 0.527777778 0.5 609
0.504788447 0.444891274 1 0.523504274 0.5 629
0.528116804 0.49535951 1 0.523504274 0.5 594
0.500631307 0.437637336 1 0.523504274 0.5 594
0.485861389 0.500468922 2 0.476495726 0.5 626
0.500034039 0.499215484 45 0.523504274 0.5 611
0.481597593 0.513566638 2 0.476495726 0.5 595
0.546684364 0.460662179 1 0.523504274 0.5 596
0.427656623 0.501290409 2 0.476495726 0.5 641
0.500013641 0.498300445 25 0.523504274 0.5 630
0.494358168 0.586759784 2 0.476495726 0.5 593
0.498752041 0.500019909 32 0.474893162 0.5 627
0.465080755 0.535760162 2 0.476495726 0.5 596
0.498437675 0.500153719 40 0.440705128 0.5 626
0.509339747 0.443358025 1 0.523504274 0.5 595
0.499517264 0.500085465 38 0.692307692 0.5 658
0.503373836 0.422931804 1 0.523504274 0.5 595
0.49924036 0.500102719 38 0.487713675 0.5 606
0.540044656 0.471330099 1 0.523504274 0.5 625
0.499193466 0.500136424 32 0.555555556 0.5 596
0.499392312 0.500113865 42 0.495726496 0.5 609
0.498284729 0.500247629 38 0.474893162 0.5 610
0.498536976 0.500248217 32 0.516559829 0.5 595
0.519832396 0.341695103 1 0.523504274 0.5 611
0.495053607 0.512316261 2 0.476495726 0.5 615
0.555819635 0.44495388 1 0.523504274 0.5 631
0.50023755 0.497268475 35 0.523504274 0.5 593
0.467068797 0.544269912 2 0.476495726 0.5 627
0.499860123 0.500462618 42 0.689102564 0.5 610
0.438525757 0.502412946 2 0.476495726 0.5 611
0.506765702 0.489856114 1 0.523504274 0.5 595
0.500096629 0.499319922 39 0.523504274 0.5 610
0.467951665 0.504153244 2 0.476495726 0.5 595
0.500844151 0.499939068 37 0.523504274 0.5 626
0.500165501 0.499950768 49 0.523504274 0.5 610
0.500023194 0.484195596 11 0.523504274 0.5 612
0.477524261 0.539072898 2 0.476495726 0.5 593
0.430651292 0.569709149 2 0.476495726 0.5 643
0.493826459 0.50058657 12 0.476495726 0.5 594
0.496560692 0.619549356 2 0.476495726 0.5 642
0.500996564 0.499807973 43 0.523504274 0.5 626
0.499830708 0.502113543 36 0.528311966 0.5 611
0.541587129 0.445700761 1 0.523504274 0.5 625
0.484821875 0.552434259 2 0.476495726 0.5 627
0.498382775 0.500123454 38 0.476495726 0.5 594
0.499697447 0.501192399 22 0.665064103 0.5 612
0.500000879 0.496865675 7 0.523504274 0.5 609
0.396518345 0.528364487 2 0.476495726 0.5 611
0.500905519 0.499984344 49 0.523504274 0.5 613
0.533783103 0.493113919 1 0.523504274 0.5 626
0.422039255 0.5157101 2 0.476495726 0.5 595
0.500223606 0.499985766 53 0.523504274 0.5 626
0.482630765 0.512511172 2 0.476495726 0.5 595
0.4958738 0.533412573 2 0.476495726 0.5 619
0.469548916 0.526160058 2 0.476495726 0.5 594
0.499957166 0.50082783 36 0.586004274 0.5 627
0.500085619 0.498128468 35 0.523504274 0.5 609
0.505473439 0.499862017 27 0.523504274 0.5 636
0.518537863 0.474958201 1 0.523504274 0.5 595
0.500138202 0.497014116 33 0.523504274 0.5 610
0.440135436 0.502806165 2 0.476495726 0.5 610
0.498985154 0.500095394 34 0.646367521 0.5 611
0.499709497 0.500595476 32 0.392094017 0.5 610
0.499565383 0.515875415 16 0.476495726 0.5 634
0.508116511 0.499807103 19 0.523504274 0.5 609
0.501108699 0.499670834 45 0.523504274 0.5 611
0.497743368 0.501201279 42 0.37232906 0.5 626
0.499950226 0.501174459 24 0.502136752 0.5 623
0.487468322 0.552558608 2 0.476495726 0.5 594
0.499723253 0.50046502 54 0.563568376 0.5 611
0.499056815 0.500068197 38 0.47542735 0.5 641
0.474629425 0.537499898 2 0.476495726 0.5 602
0.517885236 0.495555642 1 0.523504274 0.5 625
0.555453424 0.447395086 1 0.523504274 0.5 611
0.512438168 0.444012841 1 0.523504274 0.5 609
0.499444236 0.501612687 28 0.477029915 0.5 605
0.523130969 0.474908342 1 0.523504274 0.5 610
0.609663789 0.486410054 1 0.523504274 0.5 642
0.544417919 0.481337208 1 0.523504274 0.5 610
0.546596269 0.473307821 1 0.523504274 0.5 612
0.501212088 0.499924083 39 0.523504274 0.5 609
0.500076624 0.49908603 45 0.523504274 0.5 624
0.45549264 0.590992582 2 0.476495726 0.5 594
0.503460046 0.439281837 1 0.523504274 0.5 595
0.577631607 0.408933223 1 0.523504274 0.5 611
0.498671227 0.50055147 38 0.394764957 0.5 595
0.510412561 0.498658303 1 0.523504274 0.5 610
0.554032471 0.480157349 1 0.523504274 0.5 626
0.500062636 0.497357465 29 0.523504274 0.5 610
0.499980653 0.506124871 8 0.476495726 0.5 643
0.523414441 0.484791526 1 0.523504274 0.5 594
0.521390362 0.464069692 1 0.523504274 0.5 642
0.518347063 0.481811319 1 0.523504274 0.5 609
0.500001079 0.499580518 69 0.523504274 0.5 647
0.5493714 0.496427077 1 0.523504274 0.5 642
0.540174901 0.465029723 1 0.523504274 0.5 594
0.496762378 0.500483536 30 0.476495726 0.5 658
0.495773686 0.51032115 2 0.476495726 0.5 600
0.499698417 0.500936902 36 0.463141026 0.5 594
0.49927937 0.502292713 24 0.491987179 0.5 627
0.435058307 0.572944807 2 0.476495726 0.5 609
0.471506519 0.50200185 2 0.476495726 0.5 596
0.499844534 0.500974137 28 0.400106838 0.5 595
0.499340318 0.501292686 42 0.556623932 0.5 641
0.500037941 0.498220198 29 0.523504274 0.5 603
0.499244277 0.500478461 36 0.520299145 0.5 610
0.500413585 0.499995355 49 0.523504274 0.5 610
0.552680549 0.495484551 1 0.523504274 0.5 612
0.539538098 0.465679239 1 0.523504274 0.5 594
0.499982953 0.502281309 26 0.576923077 0.5 595
0.499805412 0.502448365 26 0.477029915 0.5 610
0.557187377 0.457195475 1 0.523504274 0.5 595
0.49802532 0.500036183 38 0.565705128 0.5 611
0.458930932 0.526736413 2 0.476495726 0.5 610
0.497862992 0.500031155 12 0.556089744 0.5 647
0.498022827 0.550335469 2 0.476495726 0.5 610
0.449271993 0.517858917 2 0.476495726 0.5 595
0.515925205 0.489319126 1 0.523504274 0.5 621
0.488229584 0.506422349 2 0.476495726 0.5 593
0.503586716 0.499953497 29 0.523504274 0.5 612
0.518154097 0.499853069 1 0.523504274 0.5 594
0.472937364 0.541953113 2 0.476495726 0.5 594
0.500098887 0.499417732 47 0.523504274 0.5 611
0.499763684 0.504589887 12 0.476495726 0.5 626
0.495148964 0.522812243 2 0.476495726 0.5 594
0.45408476
 下面就做实验验证是否有可能,
下面就做实验验证是否有可能,
 如图中C所示,物体ma和mb相当于被分类对象,假如被分类对象minst0是ma,minst5是mb,则图C可以得出方程
如图中C所示,物体ma和mb相当于被分类对象,假如被分类对象minst0是ma,minst5是mb,则图C可以得出方程
 而图C和图D是等价的
而图C和图D是等价的
 再假设两个网络E和F引入第三方参照物X,在E中让minst0和X分类,在F中让minst5和x分类。
则有方程
再假设两个网络E和F引入第三方参照物X,在E中让minst0和X分类,在F中让minst5和x分类。
则有方程

 现在让这个网络的结构是有1个3*3的卷积核,49*30*2的节点数,将minst的图片缩小到9*9,这个网络简写作
d2(minst0,5)81-con(3*3)49-30-2-(2*k) ,k∈(0,1)
意思是用带有一个3*3卷积核,结构是49*30*2的网络让0向1,0收敛;让5向0,1收敛,二分类minst0,5的网络。
ω05的具体测量过程是
具体进样顺序
δ=0.1
初始化权重
迭代次数
minst 0-1
1
判断是否达到收敛
minst 5-1
2
判断是否达到收敛
梯度下降
minst 0-2
3
判断是否达到收敛
minst 5-2
4
判断是否达到收敛
梯度下降
……
minst 0-4999
9997
判断是否达到收敛
minst 5-4999
9998
判断是否达到收敛
梯度下降
……
如果4999图片内没有达到收敛标准再次从头循环
minst 0-1
9999
判断是否达到收敛
minst 5-1
10000
判断是否达到收敛
梯度下降
……
每当网路达到收敛标准记录迭代次数和对应的准确率测试结果
将这一过程重复199次
δ=0.01
…
δ=1e-7
收敛条件是
if (Math.abs(f2[0]-y[0])< δ && Math.abs(f2[1]-y[1])< δ )
根据前面大量的实验任何一个网络对应一个δ都有一个特征的迭代次数n,与之对应的就有一条n(δ)曲线,让n等于公式里的ω
用同样的办法做另外的两个网络
d2(minstx,0)81-con(3*3)49-30-2-(2*k) ,k∈(0,1)
意思是用同样的网络分类minst的0和一张x图片,让0向1,0收敛,让x向0,1收敛
d2(minstx,5)81-con(3*3)49-30-2-(2*k) ,k∈(0,1)
意思是用同样的网络分类minst的5和一张x图片,让x向1,0收敛,让5向0,1收敛
现在让这个网络的结构是有1个3*3的卷积核,49*30*2的节点数,将minst的图片缩小到9*9,这个网络简写作
d2(minst0,5)81-con(3*3)49-30-2-(2*k) ,k∈(0,1)
意思是用带有一个3*3卷积核,结构是49*30*2的网络让0向1,0收敛;让5向0,1收敛,二分类minst0,5的网络。
ω05的具体测量过程是
具体进样顺序
δ=0.1
初始化权重
迭代次数
minst 0-1
1
判断是否达到收敛
minst 5-1
2
判断是否达到收敛
梯度下降
minst 0-2
3
判断是否达到收敛
minst 5-2
4
判断是否达到收敛
梯度下降
……
minst 0-4999
9997
判断是否达到收敛
minst 5-4999
9998
判断是否达到收敛
梯度下降
……
如果4999图片内没有达到收敛标准再次从头循环
minst 0-1
9999
判断是否达到收敛
minst 5-1
10000
判断是否达到收敛
梯度下降
……
每当网路达到收敛标准记录迭代次数和对应的准确率测试结果
将这一过程重复199次
δ=0.01
…
δ=1e-7
收敛条件是
if (Math.abs(f2[0]-y[0])< δ && Math.abs(f2[1]-y[1])< δ )
根据前面大量的实验任何一个网络对应一个δ都有一个特征的迭代次数n,与之对应的就有一条n(δ)曲线,让n等于公式里的ω
用同样的办法做另外的两个网络
d2(minstx,0)81-con(3*3)49-30-2-(2*k) ,k∈(0,1)
意思是用同样的网络分类minst的0和一张x图片,让0向1,0收敛,让x向0,1收敛
d2(minstx,5)81-con(3*3)49-30-2-(2*k) ,k∈(0,1)
意思是用同样的网络分类minst的5和一张x图片,让x向1,0收敛,让5向0,1收敛
 相当于让三个对象两两分类,让各自成为另外两个的参照物。
ω05,ωx0,ωx5都可以通过实验测出来,k可以约掉。所以ω0,ω5,ωx都可以计算出来,具体数据
δ
实测ω05
实测ωx0
实测ωx5
计算ωx
计算ω0
计算ω5
0.1
3508.41206
2472.38693
3323.90955
2405.18568
2545.55529
11070.994
0.01
4482.32161
3167.76382
4332.09045
3113.37833
3225.10272
17139.5484
0.001
6103.9397
4400.33668
5487.79899
4151.90956
4699.45802
10911.0006
1.00E-04
8919.69849
6164.71859
7451.38693
5611.71821
6921.8395
15310.0051
9.00E-05
9349.0201
6342.79899
7405.58794
5621.06102
7440.43971
14405.7759
8.00E-05
9539.44221
6398.79899
7552.99497
5682.96375
7477.91464
15627.1984
7.00E-05
10203.4322
6637.88442
7724.74372
5788.11728
8021.23091
16511.343
6.00E-05
9851.55276
6804.88945
7680.52261
5950.32629
8179.43801
13291.6796
5.00E-05
10868.8342
7217
8680.79397
6454.36378
8335.01776
19857.1576
4.00E-05
11182.1005
7507.39196
8660.1608
6582.52029
8977.85924
16693.7807
3.00E-05
12931.1709
7946.28643
9033.28643
6724.97923
10226.2497
20419.9466
2.00E-05
14625.3216
8857.38191
10089.8794
7475.60284
11471.6203
23895.9251
1.00E-05
20225.7739
10095.7136
11588.8643
8216.42308
14418.9448
112416.706
9.00E-06
21326.7688
10820.3769
11692.2714
8556.92031
17087.2773
32070.2844
8.00E-06
23468.9447
10830.608
12298.2613
8664.223
16376.1186
#NUM!
7.00E-06
24229.2161
11451.1809
12493.6382
9006.03169
18496.5046
45459.6581
6.00E-06
27358.9749
11989.7337
12861.1256
9258.46656
21097.3907
48491.3931
5.00E-06
31394.1859
12050.6683
13186.9146
9275.91094
21565.6545
#NUM!
4.00E-06
36071.5075
13025.0905
15299.7286
10315.3927
20451.1335
#NUM!
3.00E-06
43770.6281
14325.3719
15631.196
10882.6205
27712.5188
#NUM!
2.00E-06
53362.9598
15382.9698
17096.2412
11707.2494
29415.371
#NUM!
1.00E-06
76472.8291
19339.2412
21160.8241
14530.965
40438.7682
#NUM!
9.00E-07
86231.8492
20197.5528
20843.5578
14714.4894
59331.1441
#NUM!
8.00E-07
91895.4472
19328.6583
20997.8492
14394.3721
43558.2461
#NUM!
7.00E-07
94373.5528
21669.5729
21982.2714
15642.6219
76152.8888
138511.699
6.00E-07
101428.583
23628.8191
24435.0251
17229.2827
68447.7713
#NUM!
5.00E-07
95963.7688
24159.4422
24493.1256
17483.1843
80334.2167
126770.12
4.00E-07
112533.327
24202.1357
27362.5528
18368.2731
47110.8355
#NUM!
3.00E-07
120549.251
30488.2161
30380.2714
21871.4863
127875.017
114353.599
2.00E-07
135646.754
35339.0101
32491.4573
24299.0927
#NUM!
70560.5981
1.00E-07
159863.347
41935.7035
43337.4673
30686.5925
115224.791
583311.258
比较计算出来的ω0,ω5的曲线
相当于让三个对象两两分类,让各自成为另外两个的参照物。
ω05,ωx0,ωx5都可以通过实验测出来,k可以约掉。所以ω0,ω5,ωx都可以计算出来,具体数据
δ
实测ω05
实测ωx0
实测ωx5
计算ωx
计算ω0
计算ω5
0.1
3508.41206
2472.38693
3323.90955
2405.18568
2545.55529
11070.994
0.01
4482.32161
3167.76382
4332.09045
3113.37833
3225.10272
17139.5484
0.001
6103.9397
4400.33668
5487.79899
4151.90956
4699.45802
10911.0006
1.00E-04
8919.69849
6164.71859
7451.38693
5611.71821
6921.8395
15310.0051
9.00E-05
9349.0201
6342.79899
7405.58794
5621.06102
7440.43971
14405.7759
8.00E-05
9539.44221
6398.79899
7552.99497
5682.96375
7477.91464
15627.1984
7.00E-05
10203.4322
6637.88442
7724.74372
5788.11728
8021.23091
16511.343
6.00E-05
9851.55276
6804.88945
7680.52261
5950.32629
8179.43801
13291.6796
5.00E-05
10868.8342
7217
8680.79397
6454.36378
8335.01776
19857.1576
4.00E-05
11182.1005
7507.39196
8660.1608
6582.52029
8977.85924
16693.7807
3.00E-05
12931.1709
7946.28643
9033.28643
6724.97923
10226.2497
20419.9466
2.00E-05
14625.3216
8857.38191
10089.8794
7475.60284
11471.6203
23895.9251
1.00E-05
20225.7739
10095.7136
11588.8643
8216.42308
14418.9448
112416.706
9.00E-06
21326.7688
10820.3769
11692.2714
8556.92031
17087.2773
32070.2844
8.00E-06
23468.9447
10830.608
12298.2613
8664.223
16376.1186
#NUM!
7.00E-06
24229.2161
11451.1809
12493.6382
9006.03169
18496.5046
45459.6581
6.00E-06
27358.9749
11989.7337
12861.1256
9258.46656
21097.3907
48491.3931
5.00E-06
31394.1859
12050.6683
13186.9146
9275.91094
21565.6545
#NUM!
4.00E-06
36071.5075
13025.0905
15299.7286
10315.3927
20451.1335
#NUM!
3.00E-06
43770.6281
14325.3719
15631.196
10882.6205
27712.5188
#NUM!
2.00E-06
53362.9598
15382.9698
17096.2412
11707.2494
29415.371
#NUM!
1.00E-06
76472.8291
19339.2412
21160.8241
14530.965
40438.7682
#NUM!
9.00E-07
86231.8492
20197.5528
20843.5578
14714.4894
59331.1441
#NUM!
8.00E-07
91895.4472
19328.6583
20997.8492
14394.3721
43558.2461
#NUM!
7.00E-07
94373.5528
21669.5729
21982.2714
15642.6219
76152.8888
138511.699
6.00E-07
101428.583
23628.8191
24435.0251
17229.2827
68447.7713
#NUM!
5.00E-07
95963.7688
24159.4422
24493.1256
17483.1843
80334.2167
126770.12
4.00E-07
112533.327
24202.1357
27362.5528
18368.2731
47110.8355
#NUM!
3.00E-07
120549.251
30488.2161
30380.2714
21871.4863
127875.017
114353.599
2.00E-07
135646.754
35339.0101
32491.4573
24299.0927
#NUM!
70560.5981
1.00E-07
159863.347
41935.7035
43337.4673
30686.5925
115224.791
583311.258
比较计算出来的ω0,ω5的曲线
 这两条曲线是明显分开的,所以可以将它们分类,也表明神经网络的迭代次数是由参与分类的对象的特征频率合成的。
所以网络d2(minst0,5)81-con(3*3)49-30-2-(2*k) ,k∈(0,1)
的迭代次数n的精确表达式为
这两条曲线是明显分开的,所以可以将它们分类,也表明神经网络的迭代次数是由参与分类的对象的特征频率合成的。
所以网络d2(minst0,5)81-con(3*3)49-30-2-(2*k) ,k∈(0,1)
的迭代次数n的精确表达式为
 质量m0,m5,mx0,mx5,m05也可以计算出来
δ
mx
m0
m5
mxo
mx5
m05
0.1
1
0.892755
0.047198
1.892755
1.047198
0.939953
0.01
1
0.931916
0.032996
1.931916
1.032996
0.964912
0.001
1
0.780549
0.144799
1.780549
1.144799
0.925348
1.00E-04
1
0.657277
0.134351
1.657277
1.134351
0.791628
9.00E-05
1
0.570741
0.152252
1.570741
1.152252
0.722994
8.00E-05
1
0.577549
0.132248
1.577549
1.132248
0.709796
7.00E-05
1
0.520706
0.122888
1.520706
1.122888
0.643594
6.00E-05
1
0.529218
0.200411
1.529218
1.200411
0.729629
5.00E-05
1
0.599644
0.105651
1.599644
1.105651
0.705295
4.00E-05
1
0.537575
0.15548
1.537575
1.15548
0.693055
3.00E-05
1
0.432463
0.108461
1.432463
1.108461
0.540924
2.00E-05
1
0.424662
0.097869
1.424662
1.097869
0.52253
1.00E-05
1
0.324712
0.005342
1.324712
1.005342
0.330054
9.00E-06
1
0.250778
0.071192
1.250778
1.071192
0.32197
8.00E-06
1
0.279922
#NUM!
1.279922
#NUM!
#NUM!
7.00E-06
1
0.237076
0.039248
1.237076
1.039248
0.276324
6.00E-06
1
0.192584
0.036454
1.192584
1.036454
0.229038
5.00E-06
1
0.185007
#NUM!
1.185007
#NUM!
#NUM!
4.00E-06
1
0.254412
#NUM!
1.254412
#NUM!
#NUM!
3.00E-06
1
0.154211
#NUM!
1.154211
#NUM!
#NUM!
2.00E-06
1
0.158402
#NUM!
1.158402
#NUM!
#NUM!
1.00E-06
1
0.12912
#NUM!
1.12912
#NUM!
#NUM!
9.00E-07
1
0.061507
#NUM!
1.061507
#NUM!
#NUM!
8.00E-07
1
0.109206
#NUM!
1.109206
#NUM!
#NUM!
7.00E-07
1
0.042194
0.012754
1.042194
1.012754
0.054948
6.00E-07
1
0.06336
#NUM!
1.06336
#NUM!
#NUM!
5.00E-07
1
0.047363
0.01902
1.047363
1.01902
0.066383
4.00E-07
1
0.152018
#NUM!
1.152018
#NUM!
#NUM!
3.00E-07
1
0.029254
0.036581
1.029254
1.036581
0.065835
2.00E-07
1
#NUM!
0.118592
#NUM!
1.118592
#NUM!
1.00E-07
1
0.070926
0.002768
1.070926
1.002768
0.073694
质量m0,m5,mx0,mx5,m05也可以计算出来
δ
mx
m0
m5
mxo
mx5
m05
0.1
1
0.892755
0.047198
1.892755
1.047198
0.939953
0.01
1
0.931916
0.032996
1.931916
1.032996
0.964912
0.001
1
0.780549
0.144799
1.780549
1.144799
0.925348
1.00E-04
1
0.657277
0.134351
1.657277
1.134351
0.791628
9.00E-05
1
0.570741
0.152252
1.570741
1.152252
0.722994
8.00E-05
1
0.577549
0.132248
1.577549
1.132248
0.709796
7.00E-05
1
0.520706
0.122888
1.520706
1.122888
0.643594
6.00E-05
1
0.529218
0.200411
1.529218
1.200411
0.729629
5.00E-05
1
0.599644
0.105651
1.599644
1.105651
0.705295
4.00E-05
1
0.537575
0.15548
1.537575
1.15548
0.693055
3.00E-05
1
0.432463
0.108461
1.432463
1.108461
0.540924
2.00E-05
1
0.424662
0.097869
1.424662
1.097869
0.52253
1.00E-05
1
0.324712
0.005342
1.324712
1.005342
0.330054
9.00E-06
1
0.250778
0.071192
1.250778
1.071192
0.32197
8.00E-06
1
0.279922
#NUM!
1.279922
#NUM!
#NUM!
7.00E-06
1
0.237076
0.039248
1.237076
1.039248
0.276324
6.00E-06
1
0.192584
0.036454
1.192584
1.036454
0.229038
5.00E-06
1
0.185007
#NUM!
1.185007
#NUM!
#NUM!
4.00E-06
1
0.254412
#NUM!
1.254412
#NUM!
#NUM!
3.00E-06
1
0.154211
#NUM!
1.154211
#NUM!
#NUM!
2.00E-06
1
0.158402
#NUM!
1.158402
#NUM!
#NUM!
1.00E-06
1
0.12912
#NUM!
1.12912
#NUM!
#NUM!
9.00E-07
1
0.061507
#NUM!
1.061507
#NUM!
#NUM!
8.00E-07
1
0.109206
#NUM!
1.109206
#NUM!
#NUM!
7.00E-07
1
0.042194
0.012754
1.042194
1.012754
0.054948
6.00E-07
1
0.06336
#NUM!
1.06336
#NUM!
#NUM!
5.00E-07
1
0.047363
0.01902
1.047363
1.01902
0.066383
4.00E-07
1
0.152018
#NUM!
1.152018
#NUM!
#NUM!
3.00E-07
1
0.029254
0.036581
1.029254
1.036581
0.065835
2.00E-07
1
#NUM!
0.118592
#NUM!
1.118592
#NUM!
1.00E-07
1
0.070926
0.002768
1.070926
1.002768
0.073694
 minst0和minst5的质量m0和m5也是分开的。
如果让mx恒为1,则当δ=0.1时,图片集0的质量是0.892755,图片集5的质量是0.047198。
所以将神经网络理解成是一个振子动力系统在数学上是可能的,那这个系统与波粒二象性有什么关系?
minst0和minst5的质量m0和m5也是分开的。
如果让mx恒为1,则当δ=0.1时,图片集0的质量是0.892755,图片集5的质量是0.047198。
所以将神经网络理解成是一个振子动力系统在数学上是可能的,那这个系统与波粒二象性有什么关系?
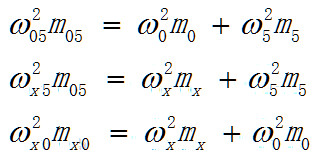 比如看这 3个方程,可以猜测如果3个被分类对象中少了任何一个,则方程仅剩下一个比如
比如看这 3个方程,可以猜测如果3个被分类对象中少了任何一个,则方程仅剩下一个比如
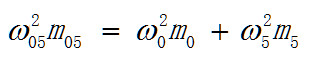 对应这个方程的解这6个未知数可能属于全体实数集,
对应这个方程的解这6个未知数可能属于全体实数集,
0.468200365 0.530903512 2 0.476495726 0.5 1423
0.498897295 0.500553235 32 0.540064103 0.5 736
0.497988522 0.500266399 40 0.472222222 0.5 704
0.437232597 0.505406109 2 0.476495726 0.5 673
0.499074493 0.50005661 38 0.450320513 0.5 658
0.491607777 0.539615398 2 0.476495726 0.5 641
0.49966528 0.500178772 34 0.563034188 0.5 657
0.498825797 0.500267978 36 0.465277778 0.5 660
0.499586943 0.579232755 2 0.476495726 0.5 609
0.499805306 0.500262273 50 0.542735043 0.5 627
0.550587527 0.492391858 1 0.523504274 0.5 610
0.494475659 0.53181447 2 0.476495726 0.5 626
0.499455292 0.501160016 42 0.408119658 0.5 642
0.499991638 0.501293813 42 0.438034188 0.5 626
0.501193324 0.499913881 21 0.523504274 0.5 610
0.500000563 0.498896864 31 0.523504274 0.5 627
0.498638626 0.501204415 42 0.503205128 0.5 610
0.499627355 0.500968078 42 0.509081197 0.5 615
0.499972285 0.500301157 46 0.409188034 0.5 626
0.478716818 0.562916511 2 0.476495726 0.5 626
0.46637963 0.514216773 2 0.476495726 0.5 610
0.528095228 0.462601235 1 0.523504274 0.5 595
0.552414594 0.462272422 1 0.523504274 0.5 616
0.484999193 0.565478321 2 0.476495726 0.5 596
0.561031885 0.446968998 1 0.523504274 0.5 625
0.498917913 0.500439205 48 0.458867521 0.5 627
0.50186706 0.499933549 45 0.523504274 0.5 610
0.490942119 0.500232783 20 0.476495726 0.5 643
0.499706075 0.500601114 50 0.527777778 0.5 609
0.504788447 0.444891274 1 0.523504274 0.5 629
0.528116804 0.49535951 1 0.523504274 0.5 594
0.500631307 0.437637336 1 0.523504274 0.5 594
0.485861389 0.500468922 2 0.476495726 0.5 626
0.500034039 0.499215484 45 0.523504274 0.5 611
0.481597593 0.513566638 2 0.476495726 0.5 595
0.546684364 0.460662179 1 0.523504274 0.5 596
0.427656623 0.501290409 2 0.476495726 0.5 641
0.500013641 0.498300445 25 0.523504274 0.5 630
0.494358168 0.586759784 2 0.476495726 0.5 593
0.498752041 0.500019909 32 0.474893162 0.5 627
0.465080755 0.535760162 2 0.476495726 0.5 596
0.498437675 0.500153719 40 0.440705128 0.5 626
0.509339747 0.443358025 1 0.523504274 0.5 595
0.499517264 0.500085465 38 0.692307692 0.5 658
0.503373836 0.422931804 1 0.523504274 0.5 595
0.49924036 0.500102719 38 0.487713675 0.5 606
0.540044656 0.471330099 1 0.523504274 0.5 625
0.499193466 0.500136424 32 0.555555556 0.5 596
0.499392312 0.500113865 42 0.495726496 0.5 609
0.498284729 0.500247629 38 0.474893162 0.5 610
0.498536976 0.500248217 32 0.516559829 0.5 595
0.519832396 0.341695103 1 0.523504274 0.5 611
0.495053607 0.512316261 2 0.476495726 0.5 615
0.555819635 0.44495388 1 0.523504274 0.5 631
0.50023755 0.497268475 35 0.523504274 0.5 593
0.467068797 0.544269912 2 0.476495726 0.5 627
0.499860123 0.500462618 42 0.689102564 0.5 610
0.438525757 0.502412946 2 0.476495726 0.5 611
0.506765702 0.489856114 1 0.523504274 0.5 595
0.500096629 0.499319922 39 0.523504274 0.5 610
0.467951665 0.504153244 2 0.476495726 0.5 595
0.500844151 0.499939068 37 0.523504274 0.5 626
0.500165501 0.499950768 49 0.523504274 0.5 610
0.500023194 0.484195596 11 0.523504274 0.5 612
0.477524261 0.539072898 2 0.476495726 0.5 593
0.430651292 0.569709149 2 0.476495726 0.5 643
0.493826459 0.50058657 12 0.476495726 0.5 594
0.496560692 0.619549356 2 0.476495726 0.5 642
0.500996564 0.499807973 43 0.523504274 0.5 626
0.499830708 0.502113543 36 0.528311966 0.5 611
0.541587129 0.445700761 1 0.523504274 0.5 625
0.484821875 0.552434259 2 0.476495726 0.5 627
0.498382775 0.500123454 38 0.476495726 0.5 594
0.499697447 0.501192399 22 0.665064103 0.5 612
0.500000879 0.496865675 7 0.523504274 0.5 609
0.396518345 0.528364487 2 0.476495726 0.5 611
0.500905519 0.499984344 49 0.523504274 0.5 613
0.533783103 0.493113919 1 0.523504274 0.5 626
0.422039255 0.5157101 2 0.476495726 0.5 595
0.500223606 0.499985766 53 0.523504274 0.5 626
0.482630765 0.512511172 2 0.476495726 0.5 595
0.4958738 0.533412573 2 0.476495726 0.5 619
0.469548916 0.526160058 2 0.476495726 0.5 594
0.499957166 0.50082783 36 0.586004274 0.5 627
0.500085619 0.498128468 35 0.523504274 0.5 609
0.505473439 0.499862017 27 0.523504274 0.5 636
0.518537863 0.474958201 1 0.523504274 0.5 595
0.500138202 0.497014116 33 0.523504274 0.5 610
0.440135436 0.502806165 2 0.476495726 0.5 610
0.498985154 0.500095394 34 0.646367521 0.5 611
0.499709497 0.500595476 32 0.392094017 0.5 610
0.499565383 0.515875415 16 0.476495726 0.5 634
0.508116511 0.499807103 19 0.523504274 0.5 609
0.501108699 0.499670834 45 0.523504274 0.5 611
0.497743368 0.501201279 42 0.37232906 0.5 626
0.499950226 0.501174459 24 0.502136752 0.5 623
0.487468322 0.552558608 2 0.476495726 0.5 594
0.499723253 0.50046502 54 0.563568376 0.5 611
0.499056815 0.500068197 38 0.47542735 0.5 641
0.474629425 0.537499898 2 0.476495726 0.5 602
0.517885236 0.495555642 1 0.523504274 0.5 625
0.555453424 0.447395086 1 0.523504274 0.5 611
0.512438168 0.444012841 1 0.523504274 0.5 609
0.499444236 0.501612687 28 0.477029915 0.5 605
0.523130969 0.474908342 1 0.523504274 0.5 610
0.609663789 0.486410054 1 0.523504274 0.5 642
0.544417919 0.481337208 1 0.523504274 0.5 610
0.546596269 0.473307821 1 0.523504274 0.5 612
0.501212088 0.499924083 39 0.523504274 0.5 609
0.500076624 0.49908603 45 0.523504274 0.5 624
0.45549264 0.590992582 2 0.476495726 0.5 594
0.503460046 0.439281837 1 0.523504274 0.5 595
0.577631607 0.408933223 1 0.523504274 0.5 611
0.498671227 0.50055147 38 0.394764957 0.5 595
0.510412561 0.498658303 1 0.523504274 0.5 610
0.554032471 0.480157349 1 0.523504274 0.5 626
0.500062636 0.497357465 29 0.523504274 0.5 610
0.499980653 0.506124871 8 0.476495726 0.5 643
0.523414441 0.484791526 1 0.523504274 0.5 594
0.521390362 0.464069692 1 0.523504274 0.5 642
0.518347063 0.481811319 1 0.523504274 0.5 609
0.500001079 0.499580518 69 0.523504274 0.5 647
0.5493714 0.496427077 1 0.523504274 0.5 642
0.540174901 0.465029723 1 0.523504274 0.5 594
0.496762378 0.500483536 30 0.476495726 0.5 658
0.495773686 0.51032115 2 0.476495726 0.5 600
0.499698417 0.500936902 36 0.463141026 0.5 594
0.49927937 0.502292713 24 0.491987179 0.5 627
0.435058307 0.572944807 2 0.476495726 0.5 609
0.471506519 0.50200185 2 0.476495726 0.5 596
0.499844534 0.500974137 28 0.400106838 0.5 595
0.499340318 0.501292686 42 0.556623932 0.5 641
0.500037941 0.498220198 29 0.523504274 0.5 603
0.499244277 0.500478461 36 0.520299145 0.5 610
0.500413585 0.499995355 49 0.523504274 0.5 610
0.552680549 0.495484551 1 0.523504274 0.5 612
0.539538098 0.465679239 1 0.523504274 0.5 594
0.499982953 0.502281309 26 0.576923077 0.5 595
0.499805412 0.502448365 26 0.477029915 0.5 610
0.557187377 0.457195475 1 0.523504274 0.5 595
0.49802532 0.500036183 38 0.565705128 0.5 611
0.458930932 0.526736413 2 0.476495726 0.5 610
0.497862992 0.500031155 12 0.556089744 0.5 647
0.498022827 0.550335469 2 0.476495726 0.5 610
0.449271993 0.517858917 2 0.476495726 0.5 595
0.515925205 0.489319126 1 0.523504274 0.5 621
0.488229584 0.506422349 2 0.476495726 0.5 593
0.503586716 0.499953497 29 0.523504274 0.5 612
0.518154097 0.499853069 1 0.523504274 0.5 594
0.472937364 0.541953113 2 0.476495726 0.5 594
0.500098887 0.499417732 47 0.523504274 0.5 611
0.499763684 0.504589887 12 0.476495726 0.5 626
0.495148964 0.522812243 2 0.476495726 0.5 594
0.45408476