RSA算法简单原理介绍（节选于网络） 假设Alice想要通过一个不可靠的媒体接收Bob的一条私人讯息。她可以用以下的方式来产生一个公钥和一个私钥：

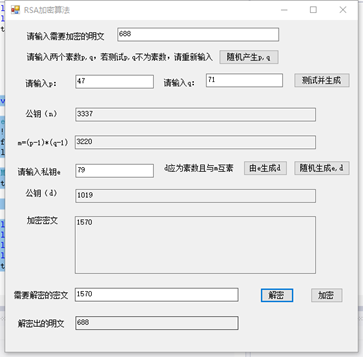
1. 随意选择两个大的质数p和q，p不等于q，计算N=pq。
2. 根据欧拉函数，求得r = (p-1)(q-1)
3. 选择一个小于 r 的整数 e，求得 e 关于模 r 的模反元素，命名为d。（模反元素存在，当且仅当e与r互质）
4. 将 p 和 q 的记录销毁。

(N,e)是公钥，(N,d)是私钥。Alice将她的公钥(N,e)传给Bob，而将她的私钥(N,d)藏起来。

加密消息

　　假设Bob想给Alice送一个消息m，他知道Alice产生的N和e。他使用起先与Alice约好的格式将m转换为一个小于N的整数n，比如他可以将每一个字转换为这个字的Unicode码，然后将这些数字连在一起组成一个数字。假如他的信息非常长的话，他可以将这个信息分为几段，然后将每一段转换为n。用下面这个公式他可以将n加密为c：

　　ne ≡ c (mod N) 计算c并不复杂。Bob算出c后就可以将它传递给Alice。

解密消息

Alice得到Bob的消息c后就可以利用她的密钥d来解码。她可以用以下这个公式来将c转换为n： 　　cd ≡ n (mod N) 得到n后，她可以将原来的信息m重新复原。 解码的原理是： 　　cd ≡ n e·d(mod N) 以及ed ≡ 1 (mod p-1)和ed ≡ 1 (mod q-1)。由费马小定理可证明（因为p和q是质数） 　　n e·d ≡ n (mod p) 　　和 　n e·d ≡ n (mod q) 这说明（因为p和q是不同的质数，所以p和q互质） 　　n e·d ≡ n (mod pq) 1 using System; 2 using System.Collections.Generic; 3 using System.ComponentModel; 4 using System.Data; 5 using System.Drawing; 6 using System.Linq; 7 using System.Text; 8 using System.Threading.Tasks; 9 using System.Windows.Forms; 10 11 namespace RSA 12 { 13 public partial class Form1 : Form 14 { 15 public Form1() 16 { 17 InitializeComponent(); 18 } 19 20 //**************************************** 21 //验证输入的p,q是否为素数，并计算n与m 22 //**************************************** 23 private void button1_Click(object sender, EventArgs e) 24 { 25 long p, q; 26 //获取p,q的值 27 p = long.Parse(textBox1.Text); 28 q = long.Parse(textBox2.Text); 29 30 //判断p，q是否为素数，若为真进行计算，则否弹出提示 31 if (isPrim(p) && isPrim(q)) 32 { 33 long n = p * q; 34 long m = (p - 1) * (q - 1); 35 textBox3.Text = n.ToString(); 36 textBox4.Text = m.ToString(); 37 } 38 else 39 { 40 MessageBox.Show("请按要求,重新输入p,q"); 41 textBox1.Clear(); 42 textBox2.Clear(); 43 textBox3.Clear(); 44 textBox1.Focus(); 45 } 46 47 48 } 49 50 //**************************************** 51 //用随机数生成素数pq，并计算n与m 52 //**************************************** 53 54 private void button5_Click(object sender, EventArgs e) 55 { 56 //生成随机数工具 57 Random random = new Random(); 58 long p, q; 59 60 //设置判断标志 61 Boolean flag = false; 62 while (!flag) 63 { 64 p = random.Next(595530); 65 q = random.Next(585530); 66 67 //若生成的两个随机数都为素数，设定更新标志，并进行显示 68 if (isPrim(p) && isPrim(q)) 69 { 70 flag = true; 71 textBox1.Text = p.ToString(); 72 textBox2.Text = q.ToString(); 73 textBox3.Clear(); 74 textBox4.Clear(); 75 } 76 77 } 78 } 79 80 //**************************************** 81 //验证输入的d是否为素数， 并计算公钥d 82 //**************************************** 83 private void button2_Click(object sender, EventArgs e) 84 { 85 //获取d,m的值 86 long d = long.Parse(textBox5.Text); 87 long m = long.Parse(textBox4.Text); 88 89 //判断输入的d是否符合条件 90 if (d > 1 && d < m && gcd(d, m) == 1 && isPrim(d)) 91 { 92 //使用逆元函数，计算d,m的逆元 93 long result = niyuan(d, m); 94 textBox6.Text = result.ToString(); 95 } 96 else 97 { 98 MessageBox.Show("输入的 e 不符合要求，请按要求,重新输入公钥 e ！"); 99 textBox5.Clear(); 100 textBox5.Focus(); 101 102 } 103 } 104 105 //**************************************** 106 //随机生成私钥d，并计算出公钥e 107 //**************************************** 108 private void button6_Click(object sender, EventArgs e) 109 { 110 long d = 0; 111 112 //获取m的值，用以计算e 113 long m = long.Parse(textBox4.Text); 114 115 //生成随机数工具，并设置随机是否完成标志 116 Random radom = new Random(); 117 Boolean flag = false; 118 while(!flag) 119 { 120 d = radom.Next(655300); 121 if (d > 1 && d < m && gcd(d, m) == 1 && isPrim(d)) 122 { 123 flag = true; 124 } 125 } 126 127 //利用逆元函数计算公钥 128 long result = niyuan(d, m); 129 130 textBox5.Text = d.ToString(); 131 textBox6.Text = result.ToString(); 132 133 } 134 135 //**************************************** 136 //利用公钥n和私钥e，加密明文 137 //**************************************** 138 private void button4_Click(object sender, EventArgs e) 139 { 140 //设置标志，判断是否已经输入明文 141 Boolean flag = false; 142 if (!string.IsNullOrWhiteSpace(textBox7.Text)) 143 flag = true; 144 145 if(flag == false) 146 { 147 MessageBox.Show("加密前,请先输入明文！"); 148 textBox7.Focus(); 149 } 150 else 151 { 152 long n = long.Parse(textBox3.Text); 153 long m = long.Parse(textBox7.Text); 154 long E = long.Parse(textBox5.Text); 155 156 //利用快速指数模运算函数生成密文 157 long C = getMod(E, m, n); 158 textBox8.Text = C.ToString(); 159 } 160 161 } 162 163 //**************************************** 164 //利用公钥n和公钥d，解密密文 165 //**************************************** 166 private void button3_Click(object sender, EventArgs e) 167 { 168 //设置标志，判断是否已经输入密文 169 Boolean flag = false; 170 if (!string.IsNullOrWhiteSpace(textBox9.Text)) 171 flag = true; 172 if(flag == false) 173 { 174 MessageBox.Show("解密前，请先输入密文！"); 175 textBox9.Focus(); 176 } 177 else 178 { 179 long C = long.Parse(textBox9.Text); 180 long n = long.Parse(textBox3.Text); 181 long d = long.Parse(textBox6.Text); 182 183 //利用快速指数模运算函数解密密文 184 long M = getMod(d, C, n); 185 textBox10.Text = M.ToString(); 186 } 187 188 } 189 190 //**************************************** 191 //输入一个数，以6为步进单元判断其是否为素数 192 //**************************************** 193 private bool isPrim(long num) 194 { 195 //两个较小数另外处理 196 if (num == 2 || num == 3) 197 return true; 198 //不在6的倍数两侧的一定不是质数 199 if (num % 6 != 1 && num % 6 != 5) 200 return false; 201 long tmp = (long)Math.Sqrt(num); 202 //在6的倍数两侧的也可能不是质数 203 for (long i = 5; i <= tmp; i += 6) 204 if (num % i == 0 || num % (i + 2) == 0) 205 return false; 206 //排除所有，剩余的是质数 207 return true; 208 } 209 210 //**************************************** 211 //采用递归的形式，判断两个数是否互质 212 //**************************************** 213 private long gcd(long x, long y) 214 { 215 return y != 0 ? gcd(y, x % y) : x; 216 } 217 218 //**************************************** 219 //利用欧几里得算法计算m，d的逆元 220 //**************************************** 221 private long niyuan(long number1, long number3) 222 { 223 long x1 = 1, x2 = 0, x3 = number3, y1 = 0, y2 = 1, y3 = number1; 224 long q; 225 long number4 = 0; 226 long t1, t2, t3; 227 while (y3 != 0) 228 { 229 if (y3 == 1) 230 { 231 number4 = y2; 232 break; 233 } 234 else 235 { 236 q = (x3 / y3); 237 t1 = x1 - q * y1; 238 t2 = x2 - q * y2; 239 t3 = x3 - q * y3; 240 x1 = y1; x2 = y2; x3 = y3; 241 y1 = t1; y2 = t2; y3 = t3; 242 } 243 } 244 if (number4 < 0) 245 number4 = number4 + number3; 246 return number4; 247 } 248 249 //**************************************** 250 //利用快速指数模运算，计算m^e mod n 251 //**************************************** 252 private long getMod(long a, long b, long c) 253 { 254 //指数 e --> a 底数 m --> b 模数 n --> c 255 long number3 = 1; 256 while (a != 0) 257 { 258 if (a % 2 == 1) 259 { 260 a = a - 1; 261 number3 = (number3 * b) % c; 262 } 263 else 264 { 265 a = (a / 2); 266 b = (b * b) % c; 267 } 268 } 269 return number3; 270 271 } 272 } 273 }