codeforces 487C Prefix Product Sequence (模逆元＋构造)

2019-04-14 20:05发布

站内文章 / 模拟电子
16713 0 1085

C. Prefix Product Sequence time limit per test 1 second memory limit per test 256 megabytes
Consider a sequence [a1, a2, ... , an]. Define its prefix product sequence . Now given n, find a permutation of[1, 2, ..., n], such that its prefix product sequence is a permutation of[0, 1, ..., n - 1]. Input The only input line contains an integer n (1 ≤ n ≤ 105). Output In the first output line, print "YES" if such sequence exists, or print "NO" if no such sequence exists. If any solution exists, you should output n more lines. i-th line contains only an integerai. The elements of the sequence should be different positive integers no larger thann. If there are multiple solutions, you are allowed to print any of them. Sample test(s) Input 7 Output YES 1 4 3 6 5 2 7 Input 6 Output NO Note For the second sample, there are no valid sequences.
题目链接：http://codeforces.com/problemset/problem/487/C
题目大意：构造一个1~n的排列  使得n个前缀积对n取余是一个0~n-1的排列
题目分析：好题，首先我们通过简单的分析可以得到n肯定是最后一个数，因为如果n在前面，前缀积肯定不止1个是n的倍数，也就是说对n取模至少有两个0，显然不满足排列，也就是说取模得到排列最后一个数是0，再来考虑前n－1个数，如果就是1 2 3 4...n-1是不是满足条件呢，显然第一个数就让它是1，是始终正确的，我们已经构造出来两个数了再来看中间的，对于一组序列a1 a2 a3 a4 ... an-1，a1=1，如果a2对n取完模要前缀积及a1*a2*a3对n取模的值与a1*a2的不同，我们不妨在a3中把a2对前缀积的影响消除，后面以此类推，这时就要用到模逆元的概念。 对于正整数和，如果有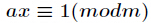，那么把这个同余方程中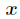的最小正整数解叫做模的逆元。如果为素数，那么还可以根据费马小定理得到逆元为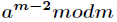。推导如下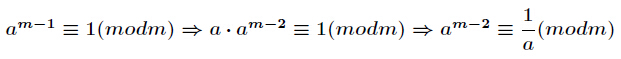： 回到本题，我们可以构造ai=(i+1)*inv[i],(inv[i]表示i的模逆元) 这样得到的前缀积a1a2a3...an-1=1*2*inv[1]*3*inv[2]*...*n*inv[n-1]因为inv[2]*2≡1(mod n)相当于前面说的消除了a2对a3的影响进一步分析，如果n是合数，则其必能表示成x*y，这里x，y是除了1和n的其他因子，因此对于前缀积(n-1)!必然能被n整除，这里有个特例4，4可以构造出1 3 2 4，原因很简单，因为4不算最后一项的前缀积为2*3显然6不能被4整除，但是比4大的最小的合数为6，6就不满足了，因为5!=2*3*4*5显然是6的倍数，当n不断扩大的时候，因子越来越多则更加能够被n整除，所以我们得到除了4以外的其他合数都无法构造出这样的序列，接下来就是怎样求模逆元的问题。 根据上面的结论了，可以用费马小定理通过快速幂取模求解模逆元，不过还有更简便的递推式 inv[i]= (n-n/i)*inv[n%i]%n，初始值inv[1]=1这个递推式的推导如下 a=n/i b=n%i  =>
 a*i+b≡0(mod n) (整除部分＋余数部分就等于n)  => -a*i≡b(mod n) (两边同除b*i)   => -a*inv[b]≡inv[i](mod n) (将a，b替换)  => -(n/i)*inv[n%i]≡inv[i](mod n) （将左边变为大于0的数，直接加上n即可,因为这时nmodn=0）  => (n-n/i)*inv[n%i]≡inv[i](mod n)  => inv[i] = (n-n/i)*inv[n%i]%n 下面给出两种解法：
 1.递推式：
 #include #include #define ll long long int const MAX = 1e5 + 10; ll inv[MAX]; int n; bool isprime(int x) { if(x == 1) return false; if(x == 2) return true; if(x % 2 == 0) return false; for(int i = 3; i <= sqrt(n); i += 2) if(n % i == 0) return false; return true; } int main() { scanf("%d", &n); if(n == 4) { printf("YES 1 3 2 4 "); return 0; } else if(n == 1) { printf("YES 1 "); return 0; } else if(!isprime(n)) { printf("NO "); return 0; } printf("YES 1 "); inv[1] = 1; for(int i = 2; i < n; i++) { inv[i] = (n - n / i) * inv[n % i] % n; printf("%lld ", ((ll) i * inv[i - 1] % n)); } printf("%d ", n); }

2.费马小定理＋快速幂取模 （速度是第1种解法的20倍）

#include #include #define ll long long int const MAX = 1e5 + 10; ll inv[MAX]; int n; bool isprime(int x) { if(x == 1) return false; if(x == 2) return true; if(x % 2 == 0) return false; for(int i = 3; i <= sqrt(n); i += 2) if(n % i == 0) return false; return true; } ll multi(ll a, ll b) { ll ans = 0; a %= n; while(b) { if(b & 1) { ans = (ans + a) % n; b--; } b >>= 1; a = (a + a) % n; } return ans; } ll quick_mod(ll a, ll b) { ll ans = 1; a %= n; while(b) { if(b & 1) { ans = multi(ans,a); b--; } b >>= 1; a = multi(a,a); } return ans; } int main() { scanf("%d", &n); if(n == 4) { printf("YES 1 3 2 4 "); return 0; } else if(n == 1) { printf("YES 1 "); return 0; } else if(!isprime(n)) { printf("NO "); return 0; } printf("YES 1 "); for(int i = 2; i < n; i++) printf("%lld ", i * quick_mod(i - 1, n - 2) % n); printf("%d ", n); }

热门文章