本文为转载,原博客地址:https://blog.csdn.net/huzq1976/article/details/51581330首先注明:如果没有特别说明,以下内容都是基于python 3.4的。先说核心要点:
1. 一个测试程序和它的输出
2. 取整和求模运算规则
3. python中其他的取整运算
4. //和math.floor在CPython中的不同
5. 运算符/在python 2 和python 3 中的区别
6. 其他讨论(求余和求模)下面按顺序介绍:1. 一个测试程序和它的输出
测试程序如下(python 3.4):
被除数=除数*商+模 (方程1)
变化一下,已知被除数和余数,模可以通过商计算出来,计算公式如下:
模=被除数-除数*商 (方程2)从wiki(https://en.wikipedia.org/wiki/Modulo_operation)查到三种不同的算法,这里拷贝了其中的一张图(只有英文版)
图1:三种不同的算法 。图中红线表示商,绿线表示模。横坐标表示被除数,纵坐标表示商或模。这幅图可以分成三行两列,共6个子图。三行trancated/floored/Euclidean division代表三种取整除法(下面会讨论);两列的解释是:第一列positive divisor, 也就是说除数是正数,第二列negative divisor,除数是负数。那这幅图到底是什么意思呢? 现在拿第二行第一列的子图解释一下 (floored division, positive divisor),这里的横坐标表示被除数,纵坐标表示商或模。这个子图中除数(divisor)是正数,当被除数也是正数时(比如前面讨论的10对4求模),商和余数都是正数或零;当被除数是负数的时候(比如之前讨论的-10对4求模),采取了向下(负数方向)取整(rounded downwards, , 函数floor的功能),本来精确除法下答案是 (-10/4 = )-2.5,现在向下取整答案是(-10//4 =) -3,也就是取整后的结果(-3)必须小于等于精确结果(-2.5), 这时用商和模的关系(方程2)很容易计算出模是2, 这也是前面例子中讨论的。这就是python采用的floored division算法,这个算法可以说是python的//和%运算符采用的最重要也是唯一的规则(当然还有abs(模) < abs(除数)),对所有的情况都适用(你可以仔细看看开始讨论的测试程序和图1中第二行的两个子图)。其它的现象都可以从这个规则中推导出来。比如我们前面说的python模运算符%的一个现象规律:模要么与除数同号,要么是零(能整除的情况下)。其本质是由python采取的向下取整算法决定的。我们只需要记住python的取整规则是:向下取整!向下取整!向下取整!另外两种:第一种truncated division,是向零取整,也就是简单粗暴地去掉小数部分,C语言采用这种方法(例子见后面的讨论)。还有一种是Euclidean division, 这里不讨论了,有兴趣的同学可以问度娘或谷哥。当然还有一种取整法,就是我们耳熟能详的四舍五入法,:)。下面接着介绍python中其它的取整方法。3.python中其他的取整运算首先说明,取整或模运算(比如a//b, a%b)中, a和b都可以是非整数,比如
-10.6//2.1=-6.0
-10.6//2.1=2.00000…这也可以归纳到上面所说的向下取整规则中,当然还有一条隐蔽规则:模的绝对值小于除数的绝对值,也就是abs(模) < abs(除数)python能够实现基本的四种取整运算:四舍五入,向零取整,向下取整和向上取整。四舍五入取整函数round
PS:Jython下可以得到20.0,而PEP里规定了a // b应该等于round(a/b),所以似乎这是cpython实现的一个bug?首先先分析下1 / 0.05究竟应该等于多少。答案就是精确的20.0。简单解释下:IEEE754浮点数规定,如果一个浮点数的值不能被精确记录,那么它的值会被记成与这个数距离最近的可以被IEEE浮点数表示的数。首先,0.05在二进制下是无限循环小数,自然不能被精确记录,因此0.05这个浮点数的实际值是不等于0.05的,实际值是约为0.05 + 2.7e-18。之后做浮点除法,实际上做的是1 / (0.05+2.7…e-18),这个除法的结果大约是20 - 1.1e-15。这个值也不能被精确表示,恰好离这个数最近的可以表示的值就是20.0,因此即使有浮点数误差结果也是精确的20.0。既然1/0.05就是20.0,那么对他做floor运算自然也是20了。现在的问题就是为什么1 // 0.05会变成19.0,要解决这个问题只能翻源码看//运算符的实现。
这里不贴源码了,结论是:cpython中x // y的实现实际上是round((x - fmod(x, y)) / y) ,其中fmod函数是求两个浮点数相除的余数。这样一来就解释的通了:在十进制下,显然1除以0.05的余数应该是0.0。然而在IEEE浮点数环境中,0.05的实际值是约0.05 + 2.7e-18,略大于0.05,这样一来1除以这个数的余数就成了约0.05 - 5e-17,从1中减掉这么多之后就只剩0.95了,除以0.05再round后变成19.0。注:这段主要参考知乎上的一篇文章(http://www.zhihu.com/question/41017093/answer/89848433),如有兴趣,大家可查看,里面有源码。5.运算符/在python 2 和python 3 中的区别//和%运算符在2和3版本中一样,但是运算符/不一样,最开始的测试程序中和运算符/有关的部分在python 2.7中的输出结果是这样的:
一篇文章(http://blog.sina.com.cn/s/blog_a3052b4a01018fd7.html)讨论求余和求模的区别 , 原文中列了一个表格,我拷贝在下面
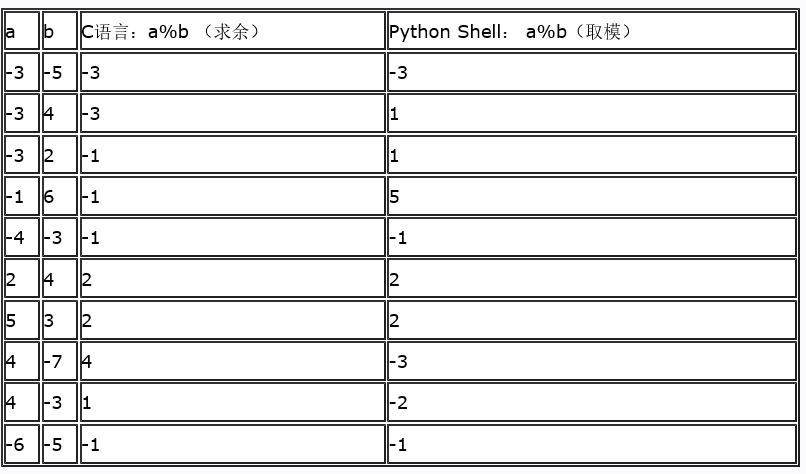
原作者认为: 取模运算时,向0 方向舍入(fix()函数); 求余运算时,向无穷小方向舍入(floor()函数)。还有一篇文章(http://www.cnblogs.com/xfzhang/archive/2010/11/25/1887214.html),讨论在matlab中取模(mod)与取余(rem)的不同。不能说这些观点本身有什么错误,matlab 也确实给出了两个不同的函数,细化了区别。但我却认为这样处理把问题复杂化了,我们没有必要在文字上钻牛角尖,非得人为区分“求余”和”求模”。我们就可以简单地认为两者相同,比如统一用”求模” 表示(当然你也可以用“求余”),只是在数学运算和不同编程语言中求模时存在不同的取整算法,主要是上面讨论的三种:truncated division, floored division, Euclidean division。 C语言用的是truncated division, 而python用的是floored division.
1. /是精确除法,//是向下取整除法,%是求模
2. %求模是基于向下取整除法规则的
3. 四舍五入取整round, 向零取整int, 向下和向上取整函数math.floor, math.ceil
4. //和math.floor在CPython中的不同
5. /在python 2 中是向下取整运算
6. C中%是向零取整求模。
- 1
- 2
- 3
- 4
- 5
- 6
- 7
1. 一个测试程序和它的输出
2. 取整和求模运算规则
3. python中其他的取整运算
4. //和math.floor在CPython中的不同
5. 运算符/在python 2 和python 3 中的区别
6. 其他讨论(求余和求模)下面按顺序介绍:1. 一个测试程序和它的输出
测试程序如下(python 3.4):
print('usage of 3 operators /, // and % in python 3.4')
print('1). usage of /')
print ('10/4 = ', 10/4)
print ('-10/4 = ', -10/4)
print ('10/-4 = ', 10/-4)
print ('-10/-4 = ', -10/-4)
print('
2). usage of //')
print ('10//4 = ', 10//4)
print ('-10//4 = ', -10//4)
print ('10//-4 = ', 10//-4)
print ('-10//-4 = ', -10//-4)
print('
3). usage of %')
print ('10%4 = ', 10%4)
print ('-10%4 = ', -10%4)
print ('10%-4 = ', 10%-4)
print ('-10%-4 = ', -10%-4)- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
usage of 3 operators /, // and % in python 3.4
1). usage of /
10/4 = 2.5
-10/4 = -2.5
10/-4 = -2.5
-10/-4 = 2.5
2). usage of //
10//4 = 2
-10//4 = -3
10//-4 = -3
-10//-4 = 2
3). usage of %
10%4 = 2
-10%4 = 2
10%-4 = -2
-10%-4 = -2- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
被除数=除数*商+模 (方程1)
变化一下,已知被除数和余数,模可以通过商计算出来,计算公式如下:
模=被除数-除数*商 (方程2)从wiki(https://en.wikipedia.org/wiki/Modulo_operation)查到三种不同的算法,这里拷贝了其中的一张图(只有英文版)

图1:三种不同的算法 。图中红线表示商,绿线表示模。横坐标表示被除数,纵坐标表示商或模。这幅图可以分成三行两列,共6个子图。三行trancated/floored/Euclidean division代表三种取整除法(下面会讨论);两列的解释是:第一列positive divisor, 也就是说除数是正数,第二列negative divisor,除数是负数。那这幅图到底是什么意思呢? 现在拿第二行第一列的子图解释一下 (floored division, positive divisor),这里的横坐标表示被除数,纵坐标表示商或模。这个子图中除数(divisor)是正数,当被除数也是正数时(比如前面讨论的10对4求模),商和余数都是正数或零;当被除数是负数的时候(比如之前讨论的-10对4求模),采取了向下(负数方向)取整(rounded downwards, , 函数floor的功能),本来精确除法下答案是 (-10/4 = )-2.5,现在向下取整答案是(-10//4 =) -3,也就是取整后的结果(-3)必须小于等于精确结果(-2.5), 这时用商和模的关系(方程2)很容易计算出模是2, 这也是前面例子中讨论的。这就是python采用的floored division算法,这个算法可以说是python的//和%运算符采用的最重要也是唯一的规则(当然还有abs(模) < abs(除数)),对所有的情况都适用(你可以仔细看看开始讨论的测试程序和图1中第二行的两个子图)。其它的现象都可以从这个规则中推导出来。比如我们前面说的python模运算符%的一个现象规律:模要么与除数同号,要么是零(能整除的情况下)。其本质是由python采取的向下取整算法决定的。我们只需要记住python的取整规则是:向下取整!向下取整!向下取整!另外两种:第一种truncated division,是向零取整,也就是简单粗暴地去掉小数部分,C语言采用这种方法(例子见后面的讨论)。还有一种是Euclidean division, 这里不讨论了,有兴趣的同学可以问度娘或谷哥。当然还有一种取整法,就是我们耳熟能详的四舍五入法,:)。下面接着介绍python中其它的取整方法。3.python中其他的取整运算首先说明,取整或模运算(比如a//b, a%b)中, a和b都可以是非整数,比如
-10.6//2.1=-6.0
-10.6//2.1=2.00000…这也可以归纳到上面所说的向下取整规则中,当然还有一条隐蔽规则:模的绝对值小于除数的绝对值,也就是abs(模) < abs(除数)python能够实现基本的四种取整运算:四舍五入,向零取整,向下取整和向上取整。四舍五入取整函数round
>>>round(3.5)
4
>>>round(-3.5)
-4
>>>round(3.49)
3
>>>round(-3.49)
-3- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
>>>int(3.99)
3
>>>int (-3.99)
-3- 1
- 2
- 3
- 4
>>>from math import floor, ceil
>>>floor(3.99)
3
>>>floor(-3.-1)
-4
>>>ceil(3.01)
4
>>>ceil(-3.99)
-3- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
>>>from math import floor
>>>3//5 == floor(3/5)
True- 1
- 2
- 3
>>>1//0.05 == floor(1/0.05)
False- 1
- 2
>>> 1/0.05
20.0
>>> 1//0.05
19.0
>>> floor(1/0.05)
20- 1
- 2
- 3
- 4
- 5
- 6
PS:Jython下可以得到20.0,而PEP里规定了a // b应该等于round(a/b),所以似乎这是cpython实现的一个bug?首先先分析下1 / 0.05究竟应该等于多少。答案就是精确的20.0。简单解释下:IEEE754浮点数规定,如果一个浮点数的值不能被精确记录,那么它的值会被记成与这个数距离最近的可以被IEEE浮点数表示的数。首先,0.05在二进制下是无限循环小数,自然不能被精确记录,因此0.05这个浮点数的实际值是不等于0.05的,实际值是约为0.05 + 2.7e-18。之后做浮点除法,实际上做的是1 / (0.05+2.7…e-18),这个除法的结果大约是20 - 1.1e-15。这个值也不能被精确表示,恰好离这个数最近的可以表示的值就是20.0,因此即使有浮点数误差结果也是精确的20.0。既然1/0.05就是20.0,那么对他做floor运算自然也是20了。现在的问题就是为什么1 // 0.05会变成19.0,要解决这个问题只能翻源码看//运算符的实现。
这里不贴源码了,结论是:cpython中x // y的实现实际上是round((x - fmod(x, y)) / y) ,其中fmod函数是求两个浮点数相除的余数。这样一来就解释的通了:在十进制下,显然1除以0.05的余数应该是0.0。然而在IEEE浮点数环境中,0.05的实际值是约0.05 + 2.7e-18,略大于0.05,这样一来1除以这个数的余数就成了约0.05 - 5e-17,从1中减掉这么多之后就只剩0.95了,除以0.05再round后变成19.0。注:这段主要参考知乎上的一篇文章(http://www.zhihu.com/question/41017093/answer/89848433),如有兴趣,大家可查看,里面有源码。5.运算符/在python 2 和python 3 中的区别//和%运算符在2和3版本中一样,但是运算符/不一样,最开始的测试程序中和运算符/有关的部分在python 2.7中的输出结果是这样的:
print ('10/4 = ', 10/4)
print ('-10/4 = ', -10/4)
print ('10/-4 = ', 10/-4)
print ('-10/-4 = ', -10/-4)('1
输出:
('10/4 = ', 2)
('-10/4 = ', -3)
('10/-4 = ', -3)
('-10/-4 = ', 2)- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
一篇文章(http://blog.sina.com.cn/s/blog_a3052b4a01018fd7.html)讨论求余和求模的区别 , 原文中列了一个表格,我拷贝在下面

原作者认为: 取模运算时,向0 方向舍入(fix()函数); 求余运算时,向无穷小方向舍入(floor()函数)。还有一篇文章(http://www.cnblogs.com/xfzhang/archive/2010/11/25/1887214.html),讨论在matlab中取模(mod)与取余(rem)的不同。不能说这些观点本身有什么错误,matlab 也确实给出了两个不同的函数,细化了区别。但我却认为这样处理把问题复杂化了,我们没有必要在文字上钻牛角尖,非得人为区分“求余”和”求模”。我们就可以简单地认为两者相同,比如统一用”求模” 表示(当然你也可以用“求余”),只是在数学运算和不同编程语言中求模时存在不同的取整算法,主要是上面讨论的三种:truncated division, floored division, Euclidean division。 C语言用的是truncated division, 而python用的是floored division.