定义1:n维实向量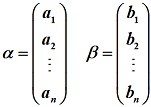 称
称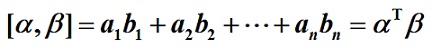 为向量
为向量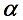 与
与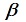 的内积
的内积

定义2:实数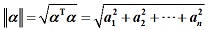 称为向量的长度(或模,或范数)。
称为向量的长度(或模,或范数)。
若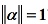 ,称
,称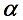 为单位向量。
为单位向量。
把向量单位化:若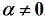 ,则
,则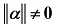 ,则
,则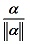 的模为1,为单位向量,称为把
的模为1,为单位向量,称为把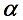 单位化。
单位化。

定义3:当向量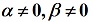 时,
时,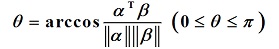 称为向量
称为向量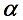 ,
,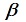 的夹角。
的夹角。
定义4:当列向量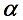 ,
,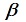 的内积为零,即
的内积为零,即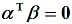 时,称向量
时,称向量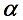 ,
,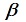 正交,记
正交,记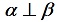
注: (1)零向量与任何向量都正交。
(2)定义了内积的向量空间称为欧氏空间。
定义5:
1) :若非零实向量组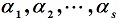 两两正交,则称其为正交向量组。
两两正交,则称其为正交向量组。
2) 若正交向量组中每个向量都是单位向量,则称其为单位正交向量组。
单位正交向量组满足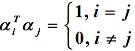
定理:正交向量组是线性无关的。(线性无关向量组未必是正交向量组)

定义6: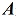 是一个n阶实矩阵,若
是一个n阶实矩阵,若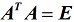 则称A为正交矩阵。
则称A为正交矩阵。
定理1:A是正交矩阵当且仅当A可逆且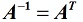

定理3:n阶实矩阵A是正交矩阵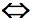 A的列(行)向量组为单位正交向量组
A的列(行)向量组为单位正交向量组
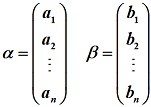 称
称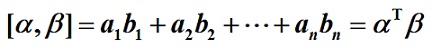 为向量
为向量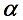 与
与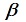 的内积
的内积

定义2:实数
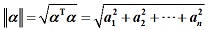 称为向量的长度(或模,或范数)。
称为向量的长度(或模,或范数)。若
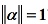 ,称
,称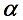 为单位向量。
为单位向量。把向量单位化:若
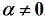 ,则
,则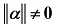 ,则
,则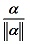 的模为1,为单位向量,称为把
的模为1,为单位向量,称为把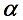 单位化。
单位化。
定义3:当向量
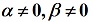 时,
时,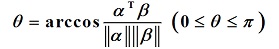 称为向量
称为向量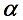 ,
,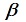 的夹角。
的夹角。定义4:当列向量
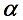 ,
,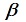 的内积为零,即
的内积为零,即 时,称向量
时,称向量 ,
, 正交,记
正交,记
注: (1)零向量与任何向量都正交。
(2)定义了内积的向量空间称为欧氏空间。
定义5:
1) :若非零实向量组
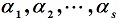 两两正交,则称其为正交向量组。
两两正交,则称其为正交向量组。2) 若正交向量组中每个向量都是单位向量,则称其为单位正交向量组。
单位正交向量组满足
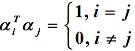
定理:正交向量组是线性无关的。(线性无关向量组未必是正交向量组)


定义6:
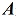 是一个n阶实矩阵,若
是一个n阶实矩阵,若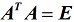 则称A为正交矩阵。
则称A为正交矩阵。定理1:A是正交矩阵当且仅当A可逆且
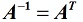

定理3:n阶实矩阵A是正交矩阵
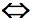 A的列(行)向量组为单位正交向量组
A的列(行)向量组为单位正交向量组