data/attach/1904/iehi70zrhpqags1gmy24myrzy6wvms5a.jpg 计算机组成与系统结构 最近因为各科都要进行期末考试，在此将本门课程各章节的一些重要的知识要点总结如下：
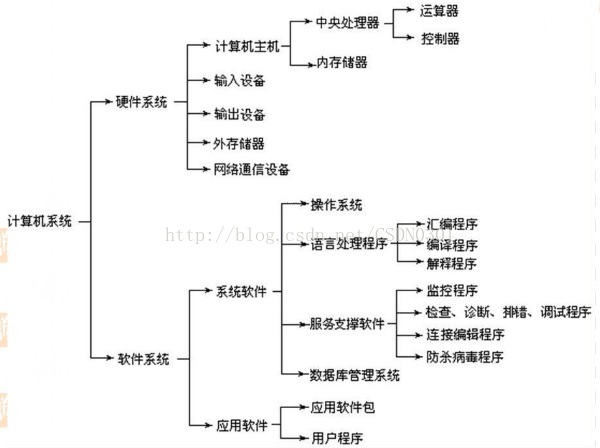
第一章：计算机系统概述 计算机系统：硬件系统+软件系统。


1.计算机的发展历经了：电子管，晶体管，小规模集成电路，大规模集成电路，巨大规模集成电路五个阶段。 2.冯.洛伊曼体系结构的特点：

1. 二进制
2. 存储程序顺序执行
3. 计算机硬件由运算器、控制器、存储器、输入设备、输出设备五部分组成
4. 将数据和指令存储在同一个存储器中。 

3.摩尔定律： 当价格不变时，集成电路上可容纳的元器件的数目，约每隔18-24个月便会增加一倍，性能也将提升一倍。
4.软件和硬件的逻辑等价性。 随着大规模集成电路和软件硬化的趋势，软件和硬件的界限将会越来越小。一些操作可以让软件实现，也可以让硬件实现。 现在应经可以把许多复杂的，常用的软件做成固件。就其功能来说，它属于软件，但就其形式来说它属于硬件。其次，现在在一块单晶硅上制作复杂的逻辑电路已经可以实现，这就为指令扩展提供了了物质基础。把本来软件做的事，换成硬件来实现。因此传统的“软件”今后可能被“固化”或者“硬化"。


  第二章：运算方法与运算器
1. IEEE754标准化数时的注意事项：

•     S：E：M=1：8
• 若是负数时，s=1，将其用绝对值进行规格化

估计说到这里很多跟我一样的孩纸最初都不明白是什么意思，下面进行两个例子来说明。      将下列十进制表示成IEEE754标准的32位浮点规格化数。       1. 27/64 2.-27/64     ok，现在开始我们真正的革命事业了：      第一步：将27/64转换成小数，接着用二进制表示     27/64=0.421875 ------>0.011011 第二步：移动小数点，使其在第一位和第二位之间（ 当尾数的值不是0时，尾数域的最高有效位应为1--这是IEEE754的规定，不要问我为什么） 可以得到：1.1011X2^-2(2的-2次方) 第三步：得出S(符号位)、E（阶码）、M（尾数）                S=0（因为是正数）      E=e+127 =125 =0111 1101（e即为第二步得到的指数 为-2）                      M=1011 0000 0000 0000 0000 000  (M为23位，当不够时填0补齐)
      第四步：得出最终结果： 00111 1101 1011 0000 0000 0000 0000 000 =（3ED80000）16
同理，当为-27/64时的步骤也是一样的，只是S=1 故最终结果:10111 1101 1011 0000 0000 0000 0000 000 =（BED80000）16
2.机器数与真值的区别？ 真值就是我们平时写的数； 机器数又被称为机器码,可以用原码，反码，补码，移码表示。 那么 问题来了，他们之间有什么联系呢？下面通过一个例子来说明这四者的关系：   例1：将十进制 -127、127分别用原码，反码，补码，移码表示.       -127  二进制真值表示：-0111 111            127 二进制真值表示：+0111 1111         原码:1111 1111 原码：0111 1111         反码:1000 0000反码：0000 0000      补码:1000 0001补码：0000 0001 移码:0000 0001移码：1000 0001 从上述的例子可以看出：原码就是符号位(最高位--此处用红 {MOD}标记)+该数的绝对值的二进制真值 反码是在原码除符号位不变，其它各位按位取反（0变1,1变0）； 补码是在反码的基础上整体加1； 移码是在反码的基础上将符号位取反,其它各位均不变。
3.浮点数的加减法运算步骤

•  0 操作检查数
• 比较阶码大小完成对阶
• 尾数进行加减运算
• 结果规格化处理
• 舍入处理  
• 判断溢出，得出最终结果

下面的一个例子可以体现上述几个步骤： 例2：设阶码3位，尾数6位，按浮点数的运算方法，完成下列取值的[x+y],[x-y].      X=2^(-011)x0.100101,Y=2^(-010)x(-0.011110)         第一步：x，y均不是0 第二步：对阶      [x]浮 =11 101 ，0.100101      [y]浮 =11 110 , 1. 100010                        此处阶码我们采用双符号位（也可以单符号位），尾数采用单符号位（也可以双符号位）        △E= [Ex]补—[Ey] 补= 11 101 + 00 010 = 11 111         即△E = —1  ，X的阶码小，应使Mx右移1位，Ex加1。      故：[X]浮=11 101，0.010010（1） 注：△E  =11  111 是补码表示，转换为真值为 -1
       第三步：尾数进行加减运算       x+y           0.010010(1) +     1.100010   —————————         1.110100(1)  第四步：规格化处理        尾数运算结果的符号位与最高数值位相同，应进行左规处理，结果为1.010010,阶码为 11 100  第五步：舍入处理 采用简单的四舍五入，最终尾数为：1.010010  第六步：判断溢出，得到最后结果                    由于阶码的符号位为11 ，故没溢出，最终结果为：2^(-100)x(-0.101110)
 x-y  的运算方法类似：
只是在第三步时：
x-y    0.010010(1)      +  0.011110 _______________________          0.110000(1)
第四步:规格化处理 由于符号位和最高数值位不相同，故不用规格化。阶码为：11 110 第五步：舍入处理 采取“0舍1入”法：故尾数结果为0.110001 所谓“0舍1入” 末尾为0直接舍弃，为1就向末位加1
第六步：判断溢出，得出结果 由于阶码符号位为 11 没有溢出，故最终结果为：2^(-010)x(0.110001)
4.用变形补码，计算x-y，x+y并判断结果是否溢出。 例：x=11011  y=-11111   [x]补 =00 11011     [y]补 =11 00001 [x+y]补= [x]补+[y]补=11 11100   由于符号位为11 ，故无溢出，x+y = -00 00100                [x-y]补 = [x]补+[-y]补=00 11011     + 00 11111  _____________________________       01 11010 最终符号位为 01 ，正溢出 ， x-y = 11010
5.基本的逻辑运算规则

•    逻辑非 运算 

例：x=01001011，求x的逻辑非。                    ~x= 10110100

•   逻辑加运算（逻辑或）

例：x=10100001   y=10011011   求x+y 1010 0001 1001 1011 ——————————— 1011 1011                           注意：逻辑或进行的不是加运算，而是或运算，什么意思呢？      就是1||1 =1 ,1||0 =1,0||1 =1,0||0 =0       归纳一哈就是:有1则结果为1，只有两个都为0时才为0

• 逻辑乘(逻辑与)

例：x= 1011 1001  y=1111 0011 ,求 x.y 1011 1001       .    1111 0011 ———————————— 1011 0001          特点：有0则为0，只有全为1时才为1

• 逻辑异或

例：x= 1011 1001  y=1111 0011 ,求 x异或y 1011 1001 xor 1111 0011   —————————— 0100 1010 特点：相同为0，相异为1

• 逻辑同或

例：x= 1010 1011  y=1111 0011 ,求 x同或y 1011 1011 xNOr 1111 0011   —————————— 1011 0111 特点：相同为1，相异为0
以上只用于个人对本阶段学习的复习，总结参考，若有不正确的地方，望各大好友指出。