1.1.3二叉树的应用
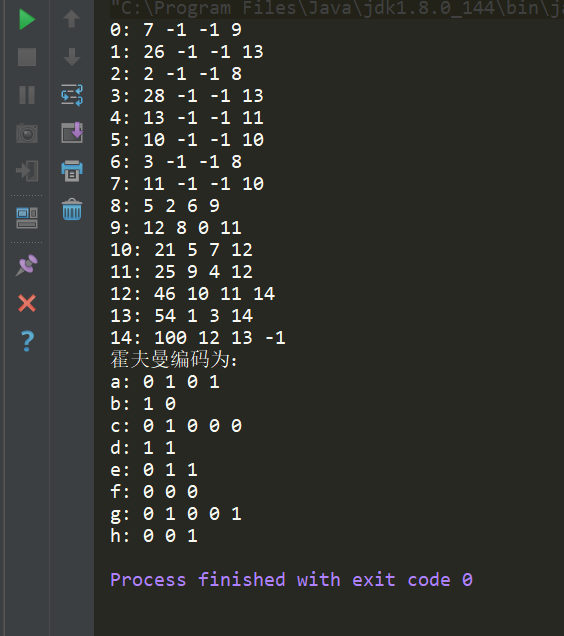
哈弗曼树的基本概念
二叉树的经典应用是哈夫曼树（Haffman）树，也称为最优二叉树 ，是指对于一组带有确定权值的叶结点，构造的具有最小带权路径长度的二叉树。
构造：
假设有n个权值，则构造出的哈夫曼树有n个叶子结点。 n个权值分别设为 w1、w2、…、wn，则哈夫曼树的构造规则为：
(1) 将w1、w2、…，wn看成是有n 棵树的森林(每棵树仅有一个结点)；
(2) 在森林中选出两个根结点的权值最小的树合并，作为一棵新树的左、右子树，且新树的根结点权值为其左、右子树根结点权值之和；
(3)从森林中删除选取的两棵树，并将新树加入森林；
(4)重复(2)、(3)步，直到森林中只剩一棵树为止，该树即为所求得的哈夫曼树 哈夫曼编码的实践
问题描述：假设通信电文使用的字符集为{a,b,c,d,e,f,g,h},各字符在电文中出现的频度分别为：7,26,2,28,13,10,3,11,编程计算出每个字符的哈夫曼编码，并通过手工绘制字符进行哈夫曼编码时所对应的哈夫曼树,计算出每个字符的哈夫曼编码，将两结果进行比较。
提示：利用上面的程序，结合实际问题修改main方法中的初始化数据，运行程序观察结果，并通过手工完成哈夫曼树的绘制，从树中提出哈夫曼编码。
设计：
1、哈夫曼数节点的设计
2、哈夫曼编码节点的设计
3，哈夫曼树的创建
4，从哈夫曼树中提出叶节点的哈夫曼编码值
代码实现： public class HFMTreeNode { int weight,parent,lchild,rchild;//该结点在霍夫曼数组中的位置 HFMTreeNode(){ weight=0; parent=lchild=rchild=-1; } } public class HFMCodeNode { int[] bit;//存储叶节点的编码0或1 int start;//标记bit数组为真正编码存储开始的位置。 HFMCodeNode(int n){//n为哈夫曼树的叶节点数目，节点数为n的哈夫曼树的长度最多为n-1个 bit=new int[n]; start=n-1; } } /** * @author刘勗 * @create2017-11-24-10:30 */ public class HFMTool { public static void main(String[] args) { char[] ch={'a','b','c','d','e','f','g','h'}; int[] weight={7,26,2,28,13,10,3,11}; int n=ch.length; HFMTreeNode[] hfmtree=new HFMTreeNode[2*n-1]; for(int i=0;i<2*n-1;i++) hfmtree[i]=new HFMTreeNode(); //给节点权值 for(int i=0;i//获得HFM编码 HFMCodeNode[] hfmcd=new HFMCodeNode[n]; for(int i=0;inew HFMCodeNode(n); createHFMCode(hfmtree,hfmcd); //输出HFM编码 System.out.println("霍夫曼编码为："); //输出每个节点的哈夫曼编码值 for(int i=0;i": "); for(int j=hfmcd[i].start+1;j" "); System.out.println(); } } public static void createHFMCode(HFMTreeNode[] hfmtree,HFMCodeNode[] cd){ int n=cd.length; for(int i=0;i//计算结点的次数 i表示树结点的位置 int c=i;//当前结点 int p=hfmtree[i].parent;//该结点的父结点 while(p!=-1){ if(hfmtree[p].lchild==c) } cd[i].bit[cd[i].start]=0； }else if(hfmtree[p].rchild==c) { cd[i].bit[cd[i].start]=1; } cd[i].start--; c=p;//父结点为当前结点 p=hfmtree[c].parent; } } } public static void pnthfmtree(HFMTreeNode[] hfmtree){ //输出哈夫曼数数组 for(int i=0;i": "+ hfmtree[i].weight+" "+hfmtree[i].lchild+" "+hfmtree[i].rchild+" "+hfmtree[i].parent); } } public static void createHFMTree(HFMTreeNode[] hfmtree,int n){ int x1,x2;//记录每次选择的两个最小值，x1 int m1,m2;//记录最小的位置 for(int i=0;i1;i++){//构建新树的次数 //选择权值最小的两个结点 x1=x2=10000;//为无穷大的值 m1=m2=0; for(int j=0;jif(hfmtree[j].parent==-1 && hfmtree[j].weightelse if(hfmtree[j].parent==-1 && hfmtree[j].weight//构建新结点 hfmtree[n+i].weight=x1+x2; hfmtree[n+i].lchild=m1; hfmtree[n+i].rchild=m2; hfmtree[m1].parent=n+i; hfmtree[m2].parent=n+i; } } }