几种坐标变换
来说一说坐标变换的问题。
我们常用的“坐标变换”,可以说是单位换算。所谓单位就是从一种衡量方式到另一种衡量方式的转换。
例如,1.2(米)等价于120(厘米),这两个是同一个概念(如图1所示)。
 图1:对乐器的两种度量
图1:对乐器的两种度量
扩展到二维,也是同样的道理。例如笛卡尔坐标系与极坐标系的转换(如图2所示)。
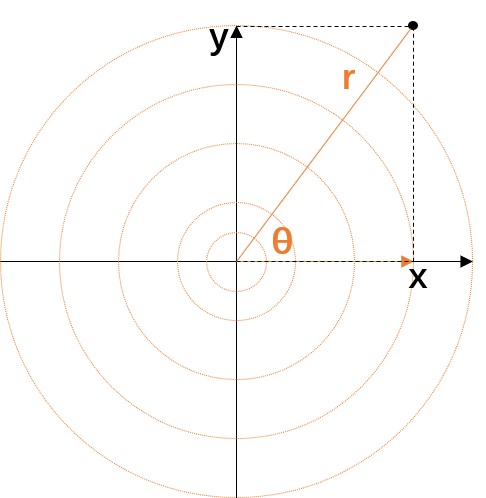 图2:笛卡尔坐标系与极坐标系的转换
图2:笛卡尔坐标系与极坐标系的转换
在笛卡尔坐标系中,黑点的位置信息可以表达为
![[3,4]_{(x,y)}](data/attach/1904/6off9gf8eyjijm9174vw8ld1hpvz1nkn.jpg)
,而在极坐标系中,黑点的位置信息可以表达为
![[5,53.1304]_{(r, heta)}](data/attach/1904/wtp282v8h23rq9i1ksnxvlfyg4y322e8.jpg)
。
两种坐标系的转换关系为:

在三相交流电系统中,三相电是三组幅值相等、频率相等、相位互相差120°的交流电(如图3所示)。
 图3:三相交流电的波形
图3:三相交流电的波形
他们的数学表达式为:



这三者相加是始终等于0的,见一下的推导:
![\V_{A}+V_{B}+V_{C}=\U_{m} cdot [sin(omega t)+sin(omega t)cos(-frac{2pi}{3})-cos(omega t)sin(frac{2pi}{3})+sin(omega t)cos(frac{2pi}{3})+cos(omega t)sin(frac{2pi}{3})]\ =U_{m} cdot [sin(omega t)(1-0.5-0.5)+cos(omega t)(-frac{sqrt{3}}{2}+frac{sqrt{3}}{2})\ =0](https://private.codecogs.com/gif.latex?%5C%5CV_%7BA%7D+V_%7BB%7D+V_%7BC%7D%3D%5C%5CU_%7Bm%7D%20%5Ccdot%20%5Bsin%28%5Comega%20t%29+sin%28%5Comega%20t%29cos%28-%5Cfrac%7B2%5Cpi%7D%7B3%7D%29-cos%28%5Comega%20t%29sin%28%5Cfrac%7B2%5Cpi%7D%7B3%7D%29+sin%28%5Comega%20t%29cos%28%5Cfrac%7B2%5Cpi%7D%7B3%7D%29+cos%28%5Comega%20t%29sin%28%5Cfrac%7B2%5Cpi%7D%7B3%7D%29%5D%5C%5C%20%3DU_%7Bm%7D%20%5Ccdot%20%5Bsin%28%5Comega%20t%29%281-0.5-0.5%29+cos%28%5Comega%20t%29%28-%5Cfrac%7B%5Csqrt%7B3%7D%7D%7B2%7D+%5Cfrac%7B%5Csqrt%7B3%7D%7D%7B2%7D%29%5C%5C%20%3D0)
然而在三相电机中,定子的线圈布置是在空间中错开120°的,空间的角度和电角度,三个固定线圈中的每一个中的正弦波电流产生垂直于旋转轴的三个正弦变化磁场(见
图4-8)。三个磁场作为矢量叠加以产生单个旋转磁场。
 图4:A相产生的幅值按正弦规律变化,方向来回变化的磁场
图4:A相产生的幅值按正弦规律变化,方向来回变化的磁场
 图5:B相产生的幅值按正弦规律变化,方向来回变化的磁场
图5:B相产生的幅值按正弦规律变化,方向来回变化的磁场
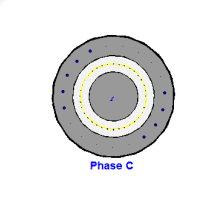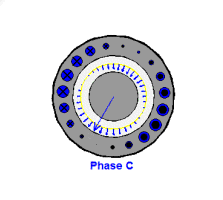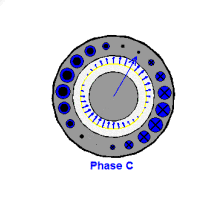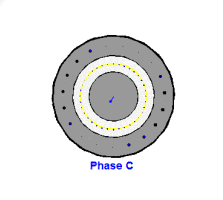 图6:C相产生的幅值按正弦规律变化,方向来回变化的磁场
图6:C相产生的幅值按正弦规律变化,方向来回变化的磁场
 图7:空间错开的三相线圈产生的矢量磁场(将磁场强度看作是电流强度的线性函数,则磁场强度按正弦规律变化)
图7:空间错开的三相线圈产生的矢量磁场(将磁场强度看作是电流强度的线性函数,则磁场强度按正弦规律变化)
最后我们会神奇的发现,这三个矢量磁场的叠加,会产生一个幅值不变的匀速旋转的磁场(见图5)。
 图8:三相磁场矢量合成产生的圆形磁场
图8:三相磁场矢量合成产生的圆形磁场
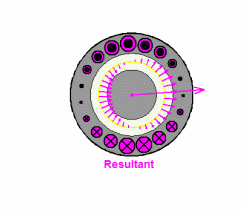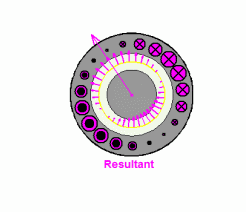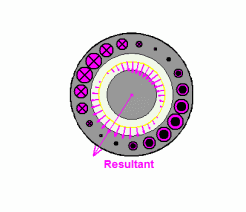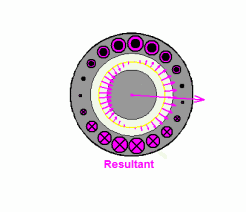 图9:合成磁场(幅值不变,匀速旋转)
图9:合成磁场(幅值不变,匀速旋转)
所以,这是一个用3个变量合成1个变量的例子。(to be continued...)


![[3,4]_{(x,y)}](data/attach/1904/6off9gf8eyjijm9174vw8ld1hpvz1nkn.jpg) ,而在极坐标系中,黑点的位置信息可以表达为
,而在极坐标系中,黑点的位置信息可以表达为![[5,53.1304]_{(r, heta)}](data/attach/1904/wtp282v8h23rq9i1ksnxvlfyg4y322e8.jpg) 。
两种坐标系的转换关系为:
。
两种坐标系的转换关系为:
 在三相交流电系统中,三相电是三组幅值相等、频率相等、相位互相差120°的交流电(如图3所示)。
在三相交流电系统中,三相电是三组幅值相等、频率相等、相位互相差120°的交流电(如图3所示)。



 这三者相加是始终等于0的,见一下的推导:
这三者相加是始终等于0的,见一下的推导:








![[3,4]_{(x,y)}](data/attach/1904/6off9gf8eyjijm9174vw8ld1hpvz1nkn.jpg) ,而在极坐标系中,黑点的位置信息可以表达为
,而在极坐标系中,黑点的位置信息可以表达为![[5,53.1304]_{(r, heta)}](data/attach/1904/wtp282v8h23rq9i1ksnxvlfyg4y322e8.jpg) 。
两种坐标系的转换关系为:
。
两种坐标系的转换关系为:
 在三相交流电系统中,三相电是三组幅值相等、频率相等、相位互相差120°的交流电(如图3所示)。
在三相交流电系统中,三相电是三组幅值相等、频率相等、相位互相差120°的交流电(如图3所示)。



 这三者相加是始终等于0的,见一下的推导:
这三者相加是始终等于0的,见一下的推导:





