§7.2 向量、向量的加减法与向量的数乘
一、向量的概念
既有大小,又有方向的量称之为向量。
数学上用一条有方向的线段(即有向线段)来表示向量。有向线段的长度表示向量的大小,有向线段的方向表示向量的方向。
以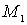 为始点,
为始点,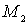 为终点的有向线段所表示的向量记为
为终点的有向线段所表示的向量记为 。
有时也有粗体字母或一个上面加有箭头的字母表示向量,如向量
。
有时也有粗体字母或一个上面加有箭头的字母表示向量,如向量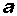 、
、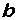 、
、 或
或  、
、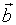 、
、 等等。
向量的大小称作向量的模。
向量
等等。
向量的大小称作向量的模。
向量 与
与 的模记作
的模记作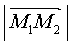 与
与 。
模等于1的向量称作单位向量。
模等于0的向量称作零向量,并记作
。
模等于1的向量称作单位向量。
模等于0的向量称作零向量,并记作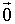 ,并规定:零向量的方向为任意的。
在直角坐标系中,以坐标原点为始点,向一点
,并规定:零向量的方向为任意的。
在直角坐标系中,以坐标原点为始点,向一点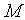 引向量,这个向量
引向量,这个向量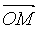 称作点
称作点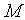 对于原点
对于原点  的向径,常用
的向径,常用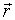 表示。
实际问题中,有些向量与始点有关,而有些向量与始点无关,但一切向量的共性是:它们都有大小和方向。因此,在数学上我们只研究与始点无关的向量,并称这种向量为自由向量,简称向量。
当遇到与始点有关的向量时(例如:质点运动的速度),可在一般原则下作特殊处理。
定义两向量
表示。
实际问题中,有些向量与始点有关,而有些向量与始点无关,但一切向量的共性是:它们都有大小和方向。因此,在数学上我们只研究与始点无关的向量,并称这种向量为自由向量,简称向量。
当遇到与始点有关的向量时(例如:质点运动的速度),可在一般原则下作特殊处理。
定义两向量 、
、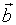 相等的意义如下:
若向量
相等的意义如下:
若向量 与向量
与向量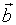 的模相等,又互相平行,且指向一致,则称向量
的模相等,又互相平行,且指向一致,则称向量 与向量
与向量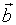 相等,并记作
相等,并记作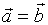 。
显然,若
。
显然,若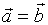 ,经过平行移动之后,
,经过平行移动之后, 与
与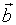 能完全重合在一起。
二、向量的加减法
据力学实验的结果,两个力的合力可根据平行四边形法则求出。
我们对向量规定加法运算如下:
设
能完全重合在一起。
二、向量的加减法
据力学实验的结果,两个力的合力可根据平行四边形法则求出。
我们对向量规定加法运算如下:
设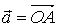 、
、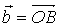 ,以
,以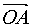 与
与 为边作一平行四边形
为边作一平行四边形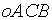 ,取对角线向量
,取对角线向量 ,记
,记 ,称
,称 为
为 与
与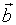 之和,并记作
之和,并记作

 这种用平行四边形的对角线向量来规定两个向量之和的方法称作向量加法的平行四边形法则。
如果向量
这种用平行四边形的对角线向量来规定两个向量之和的方法称作向量加法的平行四边形法则。
如果向量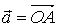 与向量
与向量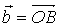 在同一直线上,那么,规定它们的和是这样一个向量:
若
在同一直线上,那么,规定它们的和是这样一个向量:
若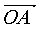 与
与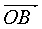 的指向相同时,和向量的方向与原来两向量相同,其模等于两向量的模之和。
的指向相同时,和向量的方向与原来两向量相同,其模等于两向量的模之和。
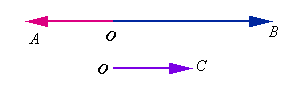
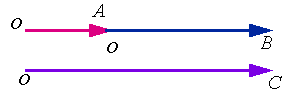 若
若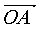 与
与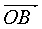 的指向相反时,和向量的模等于两向量的模之差,其方向与模值大的向量方向一致。
的指向相反时,和向量的模等于两向量的模之差,其方向与模值大的向量方向一致。
 由于平行四边形的对边平行且相等,可以这样来作出两向量的和向量:
作
由于平行四边形的对边平行且相等,可以这样来作出两向量的和向量:
作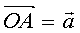 ,以
,以 的终点为起点作
的终点为起点作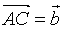 ,联接
,联接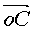 得
得
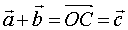 。
该方法称作向量加法的三角形法则。
。
该方法称作向量加法的三角形法则。
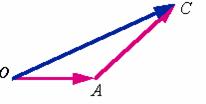 向量加法的三角形法则的实质是:
将两向量的首尾相联,则一向量的首与另一向量的尾的连线就是两向量的和向量。
据向量的加法的定义,可以证明向量加法具有下列运算规律:
1、交换律
向量加法的三角形法则的实质是:
将两向量的首尾相联,则一向量的首与另一向量的尾的连线就是两向量的和向量。
据向量的加法的定义,可以证明向量加法具有下列运算规律:
1、交换律 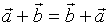 2、结合律
2、结合律 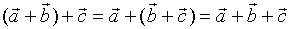
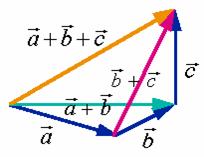 与
与 的模相同而方向相反的向量叫
的模相同而方向相反的向量叫 的负向量,记作
的负向量,记作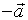 。我们规定两向量
。我们规定两向量 与
与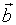 的差为:
的差为: 。
特别地,
。
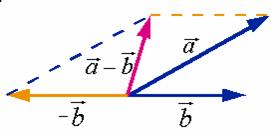
特别地,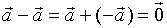 由三角形法则可看出:要从
由三角形法则可看出:要从 减去
减去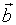 ,只要把与
,只要把与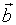 长度相同而方向相反的向量
长度相同而方向相反的向量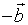 加到向量
加到向量 上去。由平行四边形法则,可如下作出向量
上去。由平行四边形法则,可如下作出向量 。
。
 三、向量与数量的乘法
设
三、向量与数量的乘法
设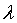 是一个数量,向量
是一个数量,向量 与
与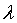 的乘积规定如下:
1、当
的乘积规定如下:
1、当 时,向量
时,向量 的方向与
的方向与 的方向相同,其模等于
的方向相同,其模等于 的
的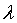 倍,
即
倍,
即 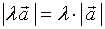 ;
2、当
;
2、当 时,向量
时,向量 是零向量,即
是零向量,即  ;
3、当
;
3、当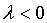 时,向量
时,向量 的方向与
的方向与 的方向相反,其模等于
的方向相反,其模等于 的
的 倍,
即
倍,
即 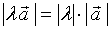 。
特别地,取
。
特别地,取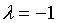 ,则向量
,则向量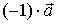 的模与
的模与 的模相等,而方向相反,由负向量的定义知:
的模相等,而方向相反,由负向量的定义知:  。
据向量与数量乘积的定义,可导出数乘向量运算符合下列运算规律:
1、结合律
。
据向量与数量乘积的定义,可导出数乘向量运算符合下列运算规律:
1、结合律 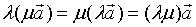 显然,向量
显然,向量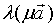 、
、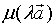 、
、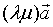 的方向是一致,
且
的方向是一致,
且 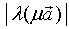 =
= 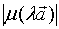 =
=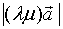 =
= 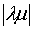 ·
· 2、分配律
2、分配律
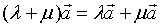
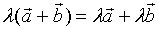 一个常用的结论:
若
一个常用的结论:
若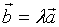 (
( 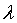 为数量 ),则向量
为数量 ),则向量 与向量
与向量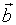 平行,记作
平行,记作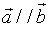 ;反之,若向量
;反之,若向量 与向量
与向量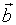 平行,则
平行,则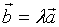 (
( 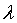 是数量)。
简言之,
是数量)。
简言之, 。
设
。
设 是非零向量,用
是非零向量,用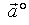 表示与
表示与 同方向的单位向量。
由于
同方向的单位向量。
由于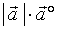 与
与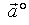 同方向,从而
同方向,从而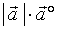 与
与 亦同方向,而且
亦同方向,而且
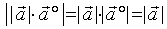 。
即
。
即 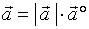 。
我们规定:若
。
我们规定:若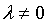 ,
, 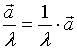 。于是
。于是 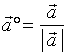 。
这表明:一个非零向量除以它的模是一个与原向量同方向的单位向量。
请注意:向量之间并没有定义除法运算,因此决不能将式子
。
这表明:一个非零向量除以它的模是一个与原向量同方向的单位向量。
请注意:向量之间并没有定义除法运算,因此决不能将式子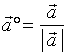 改写成形式
改写成形式 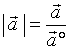 。
十分显然,这种错误是受实数运算法则的“惯性作用”所造成。
。
十分显然,这种错误是受实数运算法则的“惯性作用”所造成。
 这种用平行四边形的对角线向量来规定两个向量之和的方法称作向量加法的平行四边形法则。
如果向量
这种用平行四边形的对角线向量来规定两个向量之和的方法称作向量加法的平行四边形法则。
如果向量 若
若 由于平行四边形的对边平行且相等,可以这样来作出两向量的和向量:
作
由于平行四边形的对边平行且相等,可以这样来作出两向量的和向量:
作 向量加法的三角形法则的实质是:
将两向量的首尾相联,则一向量的首与另一向量的尾的连线就是两向量的和向量。
据向量的加法的定义,可以证明向量加法具有下列运算规律:
1、交换律
向量加法的三角形法则的实质是:
将两向量的首尾相联,则一向量的首与另一向量的尾的连线就是两向量的和向量。
据向量的加法的定义,可以证明向量加法具有下列运算规律:
1、交换律  与
与 三、向量与数量的乘法
设
三、向量与数量的乘法
设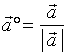 。
这表明:一个非零向量除以它的模是一个与原向量同方向的单位向量。
请注意:向量之间并没有定义除法运算,因此决不能将式子
。
这表明:一个非零向量除以它的模是一个与原向量同方向的单位向量。
请注意:向量之间并没有定义除法运算,因此决不能将式子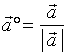 改写成形式
改写成形式