快速幂:递归形式: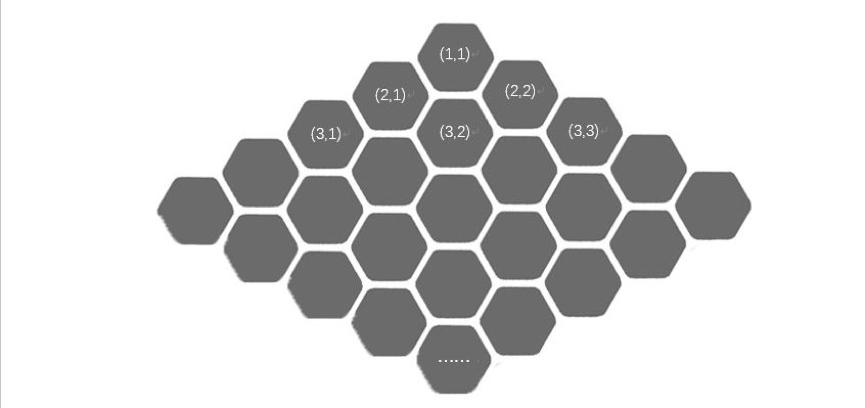 原点的坐标为(1,1),我们来分析一下、假设当前坐标为(x,y)那么向左走一步,坐标变为(x + 1,y)向下走一步,坐标变为(x + 2,y + 1)向右走一波,左边变为(x + 1, y + 1)那么从(1,1)->(x, y)我们求的就是 向左走a步、向下走b步、向右走c步有(1,1) + a *(1,0) + b (2,1) + c(1,1) == (x, y)1 + a + 2 * b + c = x ①1 + b + c = y ②进行整理有: a + b = x - y (① - ②)b + c = y - 1(②移动位置)因为x, y是直接输入的、
原点的坐标为(1,1),我们来分析一下、假设当前坐标为(x,y)那么向左走一步,坐标变为(x + 1,y)向下走一步,坐标变为(x + 2,y + 1)向右走一波,左边变为(x + 1, y + 1)那么从(1,1)->(x, y)我们求的就是 向左走a步、向下走b步、向右走c步有(1,1) + a *(1,0) + b (2,1) + c(1,1) == (x, y)1 + a + 2 * b + c = x ①1 + b + c = y ②进行整理有: a + b = x - y (① - ②)b + c = y - 1(②移动位置)因为x, y是直接输入的、
static long pow_mod(long a, long n) {
if (n == 0) {
return 1;
}
long x = pow_mod(a, n / 2);
long ans = x * x % MOD;
if ((n & 1) == 1) {
ans = ans * a % MOD;
}
return ans;
}非递归形式:static long pow_mod(long a, long n) {
long ans = 1;
while (n > 0) {
if ((n & 1) == 1) {
ans = ans * a % MOD;
}
a = a * a % MOD;
n >>= 1;
}
return ans;
}阶乘打表:static long arr[] = new long[100010];
static int MOD = 1000000007;
public static void Init() {
arr[0] = arr[1] = 1;
for (int i = 2; i <= 1e5; i++) {
arr[i] = (arr[i - 1] * i) % MOD;
}
}逆元求组合数:static long cn(int n, int m) {
return ((arr[n] * pow_mod(arr[(n - m)], MOD - 2)) % MOD * pow_mod(arr[m], MOD - 2)) % MOD;
}山东省第八届acm省赛c题 fireworks
(数学好啊、偷偷的抹一把泪)import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.io.OutputStreamWriter;
import java.io.PrintWriter;
import java.io.StreamTokenizer;
public class C {
static StreamTokenizer in = new StreamTokenizer(new BufferedReader(new InputStreamReader(System.in)));
static PrintWriter out = new PrintWriter(new OutputStreamWriter(System.out));
static int nextInt() throws IOException {
in.nextToken();
return (int) in.nval;
}
static String next() throws IOException {
in.nextToken();
return (String) in.sval;
}
static long arr[] = new long[100010];
static int MOD = 1000000007;
public static void main(String[] args) throws IOException {
int n, t, w;
Init();
while (in.nextToken() != StreamTokenizer.TT_EOF) {
n = (int) in.nval;
t = nextInt();
w = nextInt();
long ans = 0;
while (n-- > 0) {
int c, x;
x = nextInt();
c = nextInt();
int k = Math.abs(w - x);
if ((k & 1) == (t & 1) && k <= t) { // 奇偶相同(杨辉三角性质),而且在时间范围内,(一直向终点走可以到达、)
ans = (ans + (c * cn(t, (k + t) / 2)) % MOD) % MOD;
}
}
out.println(ans);
out.flush();
}
}
public static void Init() { // 阶乘打表
arr[0] = arr[1] = 1;
for (int i = 2; i <= 1e5; i++) {
arr[i] = (arr[i - 1] * i) % MOD;
}
}
static long pow_mod(long a, long n) { // 快速幂、
if (n == 0) {
return 1;
}
long x = pow_mod(a, n / 2);
long ans = x * x % MOD;
if ((n & 1) == 1) {
ans = ans * a % MOD;
}
return ans;
}
static long pow_mod1(long a, long n) { // 快速幂、
long ans = 1;
while (n > 0) {
if ((n & 1) == 1) {
ans = ans * a % MOD;
}
a = a * a % MOD;
n >>= 1;
}
return ans;
}
static long cn(int n, int m) { // 求组合数、
return ((arr[n] * pow_mod(arr[(n - m)], MOD - 2)) % MOD * pow_mod(arr[m], MOD - 2)) % MOD;
}
}山东省第八届acm省赛d题HEX 原点的坐标为(1,1),我们来分析一下、假设当前坐标为(x,y)那么向左走一步,坐标变为(x + 1,y)向下走一步,坐标变为(x + 2,y + 1)向右走一波,左边变为(x + 1, y + 1)那么从(1,1)->(x, y)我们求的就是 向左走a步、向下走b步、向右走c步有(1,1) + a *(1,0) + b (2,1) + c(1,1) == (x, y)1 + a + 2 * b + c = x ①1 + b + c = y ②进行整理有: a + b = x - y (① - ②)b + c = y - 1(②移动位置)因为x, y是直接输入的、
原点的坐标为(1,1),我们来分析一下、假设当前坐标为(x,y)那么向左走一步,坐标变为(x + 1,y)向下走一步,坐标变为(x + 2,y + 1)向右走一波,左边变为(x + 1, y + 1)那么从(1,1)->(x, y)我们求的就是 向左走a步、向下走b步、向右走c步有(1,1) + a *(1,0) + b (2,1) + c(1,1) == (x, y)1 + a + 2 * b + c = x ①1 + b + c = y ②进行整理有: a + b = x - y (① - ②)b + c = y - 1(②移动位置)因为x, y是直接输入的、import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.io.OutputStreamWriter;
import java.io.PrintWriter;
import java.io.StreamTokenizer;
public class D {
static StreamTokenizer in = new StreamTokenizer(new BufferedReader(new InputStreamReader(System.in)));
static PrintWriter out = new PrintWriter(new OutputStreamWriter(System.out));
static int nextInt() throws IOException {
in.nextToken();
return (int) in.nval;
}
static String next() throws IOException {
in.nextToken();
return (String) in.sval;
}
static long arr[] = new long[100010];
static long f[] = new long[100010];
static int MOD = 1000000007;
public static void main(String[] args) throws IOException {
int x, y;
long ans = 0;
Init();
while (in.nextToken() != StreamTokenizer.TT_EOF) {
ans = 0;
x = (int) in.nval;
y = nextInt();
int t = x - y; // a + b
int k = y - 1; // b + c
int u = Math.min(t, k);
for (int i = 0; i <= u; i++) { // 枚举 b 的所有可能走法、 (i 相当于 b)
int a = t - i;
int c = k - i;
ans += cn(i + a + c, a) * cn(i + c, i) % MOD; // C(a + b + c, a) * C(b + c, b) * C(c, c)
ans %= MOD;
}
out.println(ans);
out.flush();
}
}
public static void Init() { // 阶乘打表
arr[0] = arr[1] = 1;
for (int i = 2; i <= 1e5; i++) {
arr[i] = (arr[i - 1] * i) % MOD;
}
for(int i = 99999; i >= 0; i--) {
f[i] = pow_mod(arr[i], MOD - 2) % MOD;
}
}
static long pow_mod(long a, long n) { // 快速幂、
if (n == 0) {
return 1;
}
long x = pow_mod(a, n / 2);
long ans = x * x % MOD;
if ((n & 1) == 1) {
ans = ans * a % MOD;
}
return ans;
}
static long cn(int n, int m) { // 求组合数、
if (n == m || m == 0)
return 1;
return ((arr[n] *f[n - m]) % MOD * f[m]) % MOD;
}
}