2.7扩展欧几里德算法的应用

（3）求解模的逆元：

例如：4关于1模7的乘法逆元为多少？
4X≡1 mod 7
这个方程等价于求一个X和K，满足
4X=7K+1
其中X和K都是整数。 若ax≡1 mod f, 则称a关于模f的乘法逆元为x。
也可表示为ax≡1(mod f)。 当a与f互素时（即Gcd(a, f) = 1），a关于模f的乘法逆元有唯一解。
如果不互素，则无解。 如果f为素数，则从1到f-1的任意数都与f互素，即在1到f-1之间都恰好有一个关于模f的乘法逆元。 HDU 1576 A/B 解题思路：
设(A/B)%9973 = ans
则A/B = ans + 9973 * t1 (t1未知）
因此A = ans * B + 9973 * t1 * B 又A%9973 = n， 所以ans * B%9973 = n
故ans * B = n + 9973 * t2 (t2未知) 故(ans/n) * B +(t2/n)*9973 = gcd(B,9973) = 1 扩展欧几里得 求出ans/n, 再乘以个n，对9973取模，就是ans了 #include #include using namespace std; #define LL long long LL x, y; LL Ext_Gcd(LL a, LL b, LL &x, LL &y); int main() { // freopen("in.txt", "r" ,stdin); int T; while (cin>>T) { while (T--) { int n, B; cin>>n>>B; Ext_Gcd(B, 9973, x, y); x = (x%9973 + 9973) % 9973; int ans = x * n % 9973; cout<return 0; } LL Ext_Gcd(LL a, LL b, LL &x, LL &y) { if (b == 0) { x = 1; y = 0; return a; } LL d = Ext_Gcd(b, a%b, x, y); LL t = x; x = y; y = t - a/b*y; return d; } ZOJ 3609 Modular Inverse 注意：
结果要求为最小正整数
m=1的时候特殊处理一下，直接输出1
否则结果为0会WA #include #include using namespace std; #define LL long long LL x, y; LL Ext_Gcd(LL a, LL b, LL &x, LL &y); int main() { // freopen("in.txt", "r" ,stdin); int T; cin>>T; while (T--) { int a, m; cin>>a>>m; if (m == 1) { cout<<1<else { int d = Ext_Gcd(a, m, x, y); if (d != 1) { cout<<"Not Exist"<else { x = (x%m + m) % m; cout<return 0; } LL Ext_Gcd(LL a, LL b, LL &x, LL &y) { if (b == 0) { x = 1; y = 0; return a; } LL d = Ext_Gcd(b, a%b, x, y); LL t = x; x = y; y = t - a/b*y; return d; } 关于逆元，有一个蛮有用的性质 设p为素数，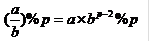

这样就可以将除法处理为乘法