数字逻辑实验报告(1)
数字逻辑实验1
一、系列二进制加法器设计50%
二、小型实验室门禁系统设计50%
总成绩
评语:(包含:预习报告内容、实验过程、实验结果及分析)
教师签名
姓 名: xxx
学 号: xxxxxxxx
班 级: 物联网1601
指 导 教 师: xxx
计算机科学与技术学院
2018年6月5日
数字逻辑实验报告
系列二进制加法器设计报告
一、系列二进制加法器设计
1、实验名称
系列二进制加法器设计。
2、实验目的
要求同学采用传统电路的设计方法,对
5种二进制加法器进行设计,并利用工具软件,例如,“logisim”软件的虚拟仿真功能来检查电路设计是否达到要求。
通过以上实验的设计、仿真、验证3个训练过程使同学们掌握传统逻辑电路的设计、仿真、调试的方法。
3、实验所用设备
Logisim2.7.1软件一套。
4、实验内容
对已设计的5种二进制加法器,使用logisim软件对它们进行虚拟实验仿真,除逻辑门、触发器外,不能直接使用logisim软件提供的逻辑库元件,具体内容如下。
(1)一位二进制半加器
设计一个一位二进制半加器,电路有两个输入A、B,两个输出S和C。输入A、B分别为被加数、加数,输出S、C为本位和、向高位进位。
(2)一位二进制全加器
设计一个一位二进制全加器,电路有三个输入A、B和Ci,两个输出S和Co。输入A、B和Ci分别为被加数、加数和来自低位的进位,输出S和Co为本位和和向高位的进位。
(3)串行进位的四位二进制并行加法器
用四个一位二进制全加器串联设计一个串行进位的四位二进制并行加法器,电路有九个输入A3、A2、A1、A0、B3、B2、B1、B0和C0,五个输出S3、S2、S1、S0和C4。输入A= A3A2A1A0、B= B3B2B1B0和C0分别为被加数、加数和来自低位的进位,输出S= S3S2S1S0和Co为本位和和向高位的进位。
(4)先行进位的四位二进制并行加法器
利用超前进位的思想设计一个先行进位的四位二进制并行加法器,电路有九个输入A3、A2、A1、A0、B3、B2、B1、B0和C0,五个输出S3、S2、S1、S0和C4。输入A= A3A2A1A0、B= B3B2B1B0和C0分别为被加数、加数和来自低位的进位,输出S= S3S2S1S0和Co为本位和和向高位的进位。
(5)将先行进位的四位二进制并行加法器封装成一个组件并验证它的正确性
将设计好的先行进位的四位二进制并行加法器进行封装,生成一个“私有”库元件并验证它的正确性,以便后续实验使用,封装后的逻辑符号参见图1-1所示。
S3 S2 S1 S0
C4 四位二进制并行加法器 C0
A3 A2 A1 A0 B3 B2 B1 B0
图1-1“私有”的先行进位的四位二进制并行加法器
5、实验方案设计
(1)一位二进制半加器的设计方案

图1-2 一位二进制半加器
(2)一位二进制全加器的设计方案
图1-3 一位二进制全加器
由真值表可得表达式为:
S=ABC+AB(-)C(-)+A(-)B(-)C+A(-)BC(-)=A⊕B⊕C
Co=A(-)BCI+ AB(-)CI+ ABC(-)i+ ABCI
(3)串行进位的四位二进制并行加法器的设计方案

图1-4串行进位的四位二进制并行加法器
函数表达式:(i=1、2、3、4)
Fi=AiBiC(i-1)+AiB(-)iC(-)(i-1)+A(-)iB(-)iC(i-1)+A(-)iBiC(-)(i-1)=Ai⊕Bi⊕C(i-1)
Ci=A(-)iBiC(i-1)+ AiB(-)iC(i-1)+ AiBiC(-)(i-1)+ AiBiC(i-1)
(4)先行进位的四位二进制并行加法器的设计方案
分析参照教材P186

图1-5先行进位的四位二进制并行加法器
(5)封装先行进位的四位二进制并行加法器电路
对“第4步”完成的电路进行封装,然后对它设计的正确性进行验证。

图1-6 四位二进制并行加法器封装验证电路
结论:通过上图电路验证,电路设计功能正确
数字逻辑实验报告
小型实验室门禁系统设计实验报告
二、小型实验室门禁系统设计
1、实验名称
小型实验室门禁系统设计。
2、实验目的
要求同学采用传统电路的设计方法,对一个“设计场景”进行逻辑电路的设计
,并利用工具软件,例如,“logisim”软件的虚拟仿真来检查这个小型实验室门禁系统的设计是否达到要求。
通过以上实验的设计、仿真、验证3个训练过程使同学们掌握小型电路系统的设计、仿真、调试方法以及电路模块封装的方法。
3、实验所用设备
Logisim2.7.1软件一套。
4、实验内容
设计场景:某小型保密实验室需要安装一个门禁系统,用于监测、控制和显示该实验室内上班人数,该实验室只有一个门,最多只能容纳15人。假设员工进出实验室都要刷校园卡,并且保证一次刷卡后有且只有一人能进出。实验室空置时人数显示为0,刷卡进入时实验室人数加1,刷卡离开时实验室人数减1。
当实验室满员时,还有员工在门外刷卡进入时,门禁系统“不”动作,系统报警提示满员。
使用logisim软件对小型电路进行虚拟实验仿真,除逻辑门、触发器、7段数码显示管外,不能直接使用logisim提供的逻辑元件库,具体要求如下。
(1)设计一个四位二进制可逆计数器电路并进行封装和验证它的正确性
用D触发器设计一个四位二进制可逆计数器,并进行封装。该计数器有一个清零端CLR、一个累加计数脉冲端CPU(输入刷卡进入请求)、一个累减计数脉冲端CPD(输入刷卡离开请求),四个计数输出端QDQCQBQA记录当前实验室人数。
将设计好的4位二进制可逆计数器进行封装,生成一个“私有”库元件,以便后续实验使用,4位二进制可逆计数器逻辑符号参见图2-1所示。
SD SC SB SA
CPU
CLR 四位二进制可逆计数器
CPD
图2-1 “私有”的一个4位二进制可逆计数器
(2)用实验1中已封装的“先行进位的四位二进制并行加法器”设计一个将实验室内人数转换成8421BCD码的电路
用实验一中已封装的“先行进位的四位二进制并行加法器”和适当的逻辑门将二进制数表示的实验室人数转换成两位十进制数的8421BCD码。
(3)设计7段译码器,并采用“7段数码显示管”显示人数的电路
设计一个7段译码器(参考书的7448芯片),将两位十进制数的8421BCD码表示的实验室人数用“7段数码显示管”显示出来。
该7段译码器有四个输入A3A2A1A0和七个输出abcdefg, A3A2A1A0为8421BCD码,abcdefg为7段数码显示管对应的段。
(4)设计当实验室满员时,门禁“不”动作,系统报警提示满员的电路
当实验室满员时,在累加计数脉冲端CPU输入刷卡进入请求,计数输出端数据保持不变,门禁“不”动作,系统报警提示满员。当实验室空时,逻辑上不会有实验室内累减计数脉冲端CPD输入刷卡离开请求。为防止信号干扰,在计数输出为0时,若CPD端有脉冲,也应使计数输出端数据保持不变,门禁“不”动作,但不用报警。
(5)设计小型实验室门禁系统电路并进行封装和验证它的正确性
设计满足要求的小型实验室门禁系统电路并进行封装,生成一个小型实验室门禁系统芯片,封装后的小型实验室门禁系统逻辑符号参见图2-2所示。
十位:7段数码显示管
个位:7段数码显示管
a b c d e f g a b c d e f g
CPU
CLR 封装后的门禁系统逻辑符号 报警
CPD
图2-2 封装后的小型实验室门禁系统
5、实验方案设计
(1)设计一个四位二进制可逆计数器电路

图2-3 一个四位二进制可逆计数器
激励函数表达式
CP1=CPU+CPD
CP2=CPU·Q1+CPD·Q1
CP3=CPU·Q1·Q2+CPD·Q1·Q2
CP4=CP3=CPU·Q1·Q2·Q3+CPD·Q1·Q2·Q3
Di=Qi(i=1,、2、3、4)
次态Qin+1=Di
(2)用实验一中已封装的“先行进位的四位二进制并行加法器”设计将实验室内人数转换成8421BCD码的电路

图2-4 一位16进制数转2位8421码
真值表:

输出函数表达式:
S7=S6=S5=0
S4=B3·(B2+B1)
S3=B3·B2·B1
S2=(B3+B1)·B2
S1=B1·B2·B3+B1·B3
S0=B0
(3)设计7段译码器,并采用“7段数码显示管”显示人数的电路
(A)设计一个7段译码器

图2-5 7段译码器
真值表:


输出a的表达式:a=A2·A1·A0+A3·A1·A0+A3·A2·A0
(b、c、d、e、f、g类似a通过真值表做卡诺图可得出)
(B)设计用“7段数码显示管”显示人数的逻辑电路

图2-6用7段数码显示管显示实验室人数的电路
参考教材P193:

 (4)设计当实验室满员时,门禁“不”动作,系统报警提示满员的电路
(4)设计当实验室满员时,门禁“不”动作,系统报警提示满员的电路
电路设计要求要采用本次实验1中由4位二进制可逆计数器所封装的“私有”库元件。

图2-7 报警电路
分析:当人数为0即现态S3S2S1S0=0000时,通过与门使累减脉冲输入无效即可实现门禁“不”动作,如图左侧;当人数为15时即S3S2S1S0=1111时,右侧与门输出1,实现满员“报警”,同时该输出通过非门后与累加脉冲相与,使其无效。
(5)设计小型实验室门禁系统电路

图2-8 门禁系统电路
6、实验结果记录
(1)给出“私有”库元件(采用一个四位二进制可逆计数器进行封装)的测试电路

图2-9 四位二进制可逆计数器测试电路
图2-10 累减脉冲测试
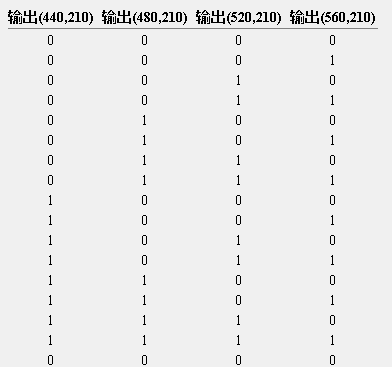
图2-10 累加脉冲测试
(2)给出采用实验1中已封装的“先行进位的四位二进制并行加法器”设计的将实验室内人数转换成8421BCD码的电路


图2-11两位二进制数的8421码测试电路
(3)给出采用“7段数码显示管”显示人数的电路
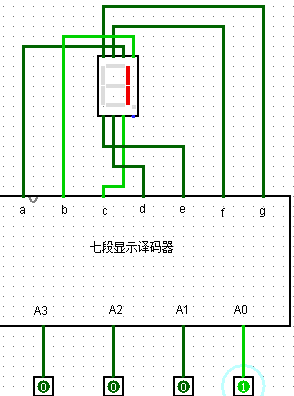

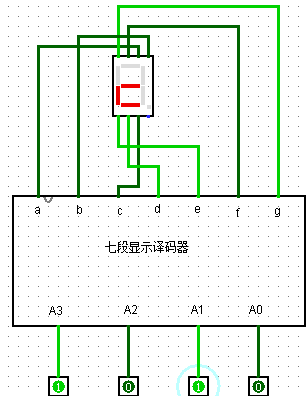
图2-12 7段数码显示管测试电路
(4)给出当实验室满员时,门禁不动作,系统报警提示满员的电路
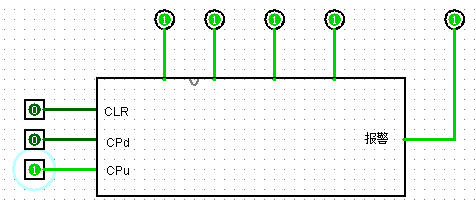
图2-13 报警测试电路
(5)给出“私有”库元件(采用小型实验室门禁系统电路进行封装)的测试电路


图2-14实验室门禁系统
电路
7、实验后的思考
(1)这两次实验的难点你认为在哪些方面?
难点一:对加法器并行与串行的正确理解。在并行加法器中,高位进位不受低位进位的影响,即每一位进位均应由输入直接得出。
难点二:四位二进制可逆计数器设计时,出现中间态。例如,假设现态为0000,在累加计数脉冲由0->1->0过程中,0->1后将产生一中间态,当由1->0后,才可得到正确的次态0001.
难点三:7段译码器输出端口多,需要逻辑门数量多且布线复杂。
(2)你是如何解决的?
解决思路:
难点一:仔细分析电路,将每一位进位的逻辑表达式化为仅含输入信号,根据表达式设计电路,切勿直接引用低位进位。
难点二:将低位D触发器的现态与脉冲输入相与来控制触发器时钟输入。使脉冲由0->1时所有触发器无时钟脉冲输入,因而使现态不变,避免了中间态的出现。具体如图2-3.
难点三:通过参考书上的真值表画出每一个输出的卡诺图,以求得其逻辑表达式。另外,不力求最少逻辑门实现,而以其与或表达式进行电路绘制,分非与或三级,便于观察与布线。具体如图2-5.
 图1-2 一位二进制半加器
(2)一位二进制全加器的设计方案
图1-3 一位二进制全加器
由真值表可得表达式为:
S=ABC+AB(-)C(-)+A(-)B(-)C+A(-)BC(-)=A⊕B⊕C
Co=A(-)BCI+ AB(-)CI+ ABC(-)i+ ABCI
(3)串行进位的四位二进制并行加法器的设计方案
图1-2 一位二进制半加器
(2)一位二进制全加器的设计方案
图1-3 一位二进制全加器
由真值表可得表达式为:
S=ABC+AB(-)C(-)+A(-)B(-)C+A(-)BC(-)=A⊕B⊕C
Co=A(-)BCI+ AB(-)CI+ ABC(-)i+ ABCI
(3)串行进位的四位二进制并行加法器的设计方案
 图1-4串行进位的四位二进制并行加法器
函数表达式:(i=1、2、3、4)
Fi=AiBiC(i-1)+AiB(-)iC(-)(i-1)+A(-)iB(-)iC(i-1)+A(-)iBiC(-)(i-1)=Ai⊕Bi⊕C(i-1)
Ci=A(-)iBiC(i-1)+ AiB(-)iC(i-1)+ AiBiC(-)(i-1)+ AiBiC(i-1)
(4)先行进位的四位二进制并行加法器的设计方案
分析参照教材P186
图1-4串行进位的四位二进制并行加法器
函数表达式:(i=1、2、3、4)
Fi=AiBiC(i-1)+AiB(-)iC(-)(i-1)+A(-)iB(-)iC(i-1)+A(-)iBiC(-)(i-1)=Ai⊕Bi⊕C(i-1)
Ci=A(-)iBiC(i-1)+ AiB(-)iC(i-1)+ AiBiC(-)(i-1)+ AiBiC(i-1)
(4)先行进位的四位二进制并行加法器的设计方案
分析参照教材P186
 图1-5先行进位的四位二进制并行加法器
(5)封装先行进位的四位二进制并行加法器电路
对“第4步”完成的电路进行封装,然后对它设计的正确性进行验证。
图1-5先行进位的四位二进制并行加法器
(5)封装先行进位的四位二进制并行加法器电路
对“第4步”完成的电路进行封装,然后对它设计的正确性进行验证。
 图1-6 四位二进制并行加法器封装验证电路
结论:通过上图电路验证,电路设计功能正确
数字逻辑实验报告
小型实验室门禁系统设计实验报告
二、小型实验室门禁系统设计
1、实验名称
小型实验室门禁系统设计。
2、实验目的
要求同学采用传统电路的设计方法,对一个“设计场景”进行逻辑电路的设计,并利用工具软件,例如,“logisim”软件的虚拟仿真来检查这个小型实验室门禁系统的设计是否达到要求。
通过以上实验的设计、仿真、验证3个训练过程使同学们掌握小型电路系统的设计、仿真、调试方法以及电路模块封装的方法。
3、实验所用设备
Logisim2.7.1软件一套。
4、实验内容
设计场景:某小型保密实验室需要安装一个门禁系统,用于监测、控制和显示该实验室内上班人数,该实验室只有一个门,最多只能容纳15人。假设员工进出实验室都要刷校园卡,并且保证一次刷卡后有且只有一人能进出。实验室空置时人数显示为0,刷卡进入时实验室人数加1,刷卡离开时实验室人数减1。
当实验室满员时,还有员工在门外刷卡进入时,门禁系统“不”动作,系统报警提示满员。
使用logisim软件对小型电路进行虚拟实验仿真,除逻辑门、触发器、7段数码显示管外,不能直接使用logisim提供的逻辑元件库,具体要求如下。
(1)设计一个四位二进制可逆计数器电路并进行封装和验证它的正确性
用D触发器设计一个四位二进制可逆计数器,并进行封装。该计数器有一个清零端CLR、一个累加计数脉冲端CPU(输入刷卡进入请求)、一个累减计数脉冲端CPD(输入刷卡离开请求),四个计数输出端QDQCQBQA记录当前实验室人数。
将设计好的4位二进制可逆计数器进行封装,生成一个“私有”库元件,以便后续实验使用,4位二进制可逆计数器逻辑符号参见图2-1所示。
SD SC SB SA
CPU
CLR 四位二进制可逆计数器
CPD
图2-1 “私有”的一个4位二进制可逆计数器
(2)用实验1中已封装的“先行进位的四位二进制并行加法器”设计一个将实验室内人数转换成8421BCD码的电路
用实验一中已封装的“先行进位的四位二进制并行加法器”和适当的逻辑门将二进制数表示的实验室人数转换成两位十进制数的8421BCD码。
(3)设计7段译码器,并采用“7段数码显示管”显示人数的电路
设计一个7段译码器(参考书的7448芯片),将两位十进制数的8421BCD码表示的实验室人数用“7段数码显示管”显示出来。
该7段译码器有四个输入A3A2A1A0和七个输出abcdefg, A3A2A1A0为8421BCD码,abcdefg为7段数码显示管对应的段。
(4)设计当实验室满员时,门禁“不”动作,系统报警提示满员的电路
当实验室满员时,在累加计数脉冲端CPU输入刷卡进入请求,计数输出端数据保持不变,门禁“不”动作,系统报警提示满员。当实验室空时,逻辑上不会有实验室内累减计数脉冲端CPD输入刷卡离开请求。为防止信号干扰,在计数输出为0时,若CPD端有脉冲,也应使计数输出端数据保持不变,门禁“不”动作,但不用报警。
(5)设计小型实验室门禁系统电路并进行封装和验证它的正确性
设计满足要求的小型实验室门禁系统电路并进行封装,生成一个小型实验室门禁系统芯片,封装后的小型实验室门禁系统逻辑符号参见图2-2所示。
十位:7段数码显示管
个位:7段数码显示管
a b c d e f g a b c d e f g
CPU
CLR 封装后的门禁系统逻辑符号 报警
CPD
图2-2 封装后的小型实验室门禁系统
5、实验方案设计
(1)设计一个四位二进制可逆计数器电路
图1-6 四位二进制并行加法器封装验证电路
结论:通过上图电路验证,电路设计功能正确
数字逻辑实验报告
小型实验室门禁系统设计实验报告
二、小型实验室门禁系统设计
1、实验名称
小型实验室门禁系统设计。
2、实验目的
要求同学采用传统电路的设计方法,对一个“设计场景”进行逻辑电路的设计,并利用工具软件,例如,“logisim”软件的虚拟仿真来检查这个小型实验室门禁系统的设计是否达到要求。
通过以上实验的设计、仿真、验证3个训练过程使同学们掌握小型电路系统的设计、仿真、调试方法以及电路模块封装的方法。
3、实验所用设备
Logisim2.7.1软件一套。
4、实验内容
设计场景:某小型保密实验室需要安装一个门禁系统,用于监测、控制和显示该实验室内上班人数,该实验室只有一个门,最多只能容纳15人。假设员工进出实验室都要刷校园卡,并且保证一次刷卡后有且只有一人能进出。实验室空置时人数显示为0,刷卡进入时实验室人数加1,刷卡离开时实验室人数减1。
当实验室满员时,还有员工在门外刷卡进入时,门禁系统“不”动作,系统报警提示满员。
使用logisim软件对小型电路进行虚拟实验仿真,除逻辑门、触发器、7段数码显示管外,不能直接使用logisim提供的逻辑元件库,具体要求如下。
(1)设计一个四位二进制可逆计数器电路并进行封装和验证它的正确性
用D触发器设计一个四位二进制可逆计数器,并进行封装。该计数器有一个清零端CLR、一个累加计数脉冲端CPU(输入刷卡进入请求)、一个累减计数脉冲端CPD(输入刷卡离开请求),四个计数输出端QDQCQBQA记录当前实验室人数。
将设计好的4位二进制可逆计数器进行封装,生成一个“私有”库元件,以便后续实验使用,4位二进制可逆计数器逻辑符号参见图2-1所示。
SD SC SB SA
CPU
CLR 四位二进制可逆计数器
CPD
图2-1 “私有”的一个4位二进制可逆计数器
(2)用实验1中已封装的“先行进位的四位二进制并行加法器”设计一个将实验室内人数转换成8421BCD码的电路
用实验一中已封装的“先行进位的四位二进制并行加法器”和适当的逻辑门将二进制数表示的实验室人数转换成两位十进制数的8421BCD码。
(3)设计7段译码器,并采用“7段数码显示管”显示人数的电路
设计一个7段译码器(参考书的7448芯片),将两位十进制数的8421BCD码表示的实验室人数用“7段数码显示管”显示出来。
该7段译码器有四个输入A3A2A1A0和七个输出abcdefg, A3A2A1A0为8421BCD码,abcdefg为7段数码显示管对应的段。
(4)设计当实验室满员时,门禁“不”动作,系统报警提示满员的电路
当实验室满员时,在累加计数脉冲端CPU输入刷卡进入请求,计数输出端数据保持不变,门禁“不”动作,系统报警提示满员。当实验室空时,逻辑上不会有实验室内累减计数脉冲端CPD输入刷卡离开请求。为防止信号干扰,在计数输出为0时,若CPD端有脉冲,也应使计数输出端数据保持不变,门禁“不”动作,但不用报警。
(5)设计小型实验室门禁系统电路并进行封装和验证它的正确性
设计满足要求的小型实验室门禁系统电路并进行封装,生成一个小型实验室门禁系统芯片,封装后的小型实验室门禁系统逻辑符号参见图2-2所示。
十位:7段数码显示管
个位:7段数码显示管
a b c d e f g a b c d e f g
CPU
CLR 封装后的门禁系统逻辑符号 报警
CPD
图2-2 封装后的小型实验室门禁系统
5、实验方案设计
(1)设计一个四位二进制可逆计数器电路
 图2-3 一个四位二进制可逆计数器
激励函数表达式
CP1=CPU+CPD
CP2=CPU·Q1+CPD·Q1
CP3=CPU·Q1·Q2+CPD·Q1·Q2
CP4=CP3=CPU·Q1·Q2·Q3+CPD·Q1·Q2·Q3
Di=Qi(i=1,、2、3、4)
次态Qin+1=Di
(2)用实验一中已封装的“先行进位的四位二进制并行加法器”设计将实验室内人数转换成8421BCD码的电路
图2-3 一个四位二进制可逆计数器
激励函数表达式
CP1=CPU+CPD
CP2=CPU·Q1+CPD·Q1
CP3=CPU·Q1·Q2+CPD·Q1·Q2
CP4=CP3=CPU·Q1·Q2·Q3+CPD·Q1·Q2·Q3
Di=Qi(i=1,、2、3、4)
次态Qin+1=Di
(2)用实验一中已封装的“先行进位的四位二进制并行加法器”设计将实验室内人数转换成8421BCD码的电路
 图2-4 一位16进制数转2位8421码
真值表:
图2-4 一位16进制数转2位8421码
真值表:
 输出函数表达式:
S7=S6=S5=0
S4=B3·(B2+B1)
S3=B3·B2·B1
S2=(B3+B1)·B2
S1=B1·B2·B3+B1·B3
S0=B0
(3)设计7段译码器,并采用“7段数码显示管”显示人数的电路
(A)设计一个7段译码器
输出函数表达式:
S7=S6=S5=0
S4=B3·(B2+B1)
S3=B3·B2·B1
S2=(B3+B1)·B2
S1=B1·B2·B3+B1·B3
S0=B0
(3)设计7段译码器,并采用“7段数码显示管”显示人数的电路
(A)设计一个7段译码器
 图2-5 7段译码器
真值表:
图2-5 7段译码器
真值表:

 输出a的表达式:a=A2·A1·A0+A3·A1·A0+A3·A2·A0
(b、c、d、e、f、g类似a通过真值表做卡诺图可得出)
(B)设计用“7段数码显示管”显示人数的逻辑电路
输出a的表达式:a=A2·A1·A0+A3·A1·A0+A3·A2·A0
(b、c、d、e、f、g类似a通过真值表做卡诺图可得出)
(B)设计用“7段数码显示管”显示人数的逻辑电路
 图2-6用7段数码显示管显示实验室人数的电路
参考教材P193:
图2-6用7段数码显示管显示实验室人数的电路
参考教材P193:

 (4)设计当实验室满员时,门禁“不”动作,系统报警提示满员的电路
电路设计要求要采用本次实验1中由4位二进制可逆计数器所封装的“私有”库元件。
(4)设计当实验室满员时,门禁“不”动作,系统报警提示满员的电路
电路设计要求要采用本次实验1中由4位二进制可逆计数器所封装的“私有”库元件。
 图2-7 报警电路
分析:当人数为0即现态S3S2S1S0=0000时,通过与门使累减脉冲输入无效即可实现门禁“不”动作,如图左侧;当人数为15时即S3S2S1S0=1111时,右侧与门输出1,实现满员“报警”,同时该输出通过非门后与累加脉冲相与,使其无效。
(5)设计小型实验室门禁系统电路
图2-7 报警电路
分析:当人数为0即现态S3S2S1S0=0000时,通过与门使累减脉冲输入无效即可实现门禁“不”动作,如图左侧;当人数为15时即S3S2S1S0=1111时,右侧与门输出1,实现满员“报警”,同时该输出通过非门后与累加脉冲相与,使其无效。
(5)设计小型实验室门禁系统电路
 图2-8 门禁系统电路
6、实验结果记录
(1)给出“私有”库元件(采用一个四位二进制可逆计数器进行封装)的测试电路
图2-8 门禁系统电路
6、实验结果记录
(1)给出“私有”库元件(采用一个四位二进制可逆计数器进行封装)的测试电路
 图2-9 四位二进制可逆计数器测试电路
图2-10 累减脉冲测试
图2-9 四位二进制可逆计数器测试电路
图2-10 累减脉冲测试
 图2-10 累加脉冲测试
(2)给出采用实验1中已封装的“先行进位的四位二进制并行加法器”设计的将实验室内人数转换成8421BCD码的电路
图2-10 累加脉冲测试
(2)给出采用实验1中已封装的“先行进位的四位二进制并行加法器”设计的将实验室内人数转换成8421BCD码的电路

 图2-11两位二进制数的8421码测试电路
(3)给出采用“7段数码显示管”显示人数的电路
图2-11两位二进制数的8421码测试电路
(3)给出采用“7段数码显示管”显示人数的电路


 图2-12 7段数码显示管测试电路
(4)给出当实验室满员时,门禁不动作,系统报警提示满员的电路
图2-12 7段数码显示管测试电路
(4)给出当实验室满员时,门禁不动作,系统报警提示满员的电路
 图2-13 报警测试电路
(5)给出“私有”库元件(采用小型实验室门禁系统电路进行封装)的测试电路
图2-13 报警测试电路
(5)给出“私有”库元件(采用小型实验室门禁系统电路进行封装)的测试电路

 图2-14实验室门禁系统电路
7、实验后的思考
(1)这两次实验的难点你认为在哪些方面?
难点一:对加法器并行与串行的正确理解。在并行加法器中,高位进位不受低位进位的影响,即每一位进位均应由输入直接得出。
难点二:四位二进制可逆计数器设计时,出现中间态。例如,假设现态为0000,在累加计数脉冲由0->1->0过程中,0->1后将产生一中间态,当由1->0后,才可得到正确的次态0001.
难点三:7段译码器输出端口多,需要逻辑门数量多且布线复杂。
(2)你是如何解决的?
解决思路:
难点一:仔细分析电路,将每一位进位的逻辑表达式化为仅含输入信号,根据表达式设计电路,切勿直接引用低位进位。
难点二:将低位D触发器的现态与脉冲输入相与来控制触发器时钟输入。使脉冲由0->1时所有触发器无时钟脉冲输入,因而使现态不变,避免了中间态的出现。具体如图2-3.
难点三:通过参考书上的真值表画出每一个输出的卡诺图,以求得其逻辑表达式。另外,不力求最少逻辑门实现,而以其与或表达式进行电路绘制,分非与或三级,便于观察与布线。具体如图2-5.
图2-14实验室门禁系统电路
7、实验后的思考
(1)这两次实验的难点你认为在哪些方面?
难点一:对加法器并行与串行的正确理解。在并行加法器中,高位进位不受低位进位的影响,即每一位进位均应由输入直接得出。
难点二:四位二进制可逆计数器设计时,出现中间态。例如,假设现态为0000,在累加计数脉冲由0->1->0过程中,0->1后将产生一中间态,当由1->0后,才可得到正确的次态0001.
难点三:7段译码器输出端口多,需要逻辑门数量多且布线复杂。
(2)你是如何解决的?
解决思路:
难点一:仔细分析电路,将每一位进位的逻辑表达式化为仅含输入信号,根据表达式设计电路,切勿直接引用低位进位。
难点二:将低位D触发器的现态与脉冲输入相与来控制触发器时钟输入。使脉冲由0->1时所有触发器无时钟脉冲输入,因而使现态不变,避免了中间态的出现。具体如图2-3.
难点三:通过参考书上的真值表画出每一个输出的卡诺图,以求得其逻辑表达式。另外,不力求最少逻辑门实现,而以其与或表达式进行电路绘制,分非与或三级,便于观察与布线。具体如图2-5.