在平面解析几何中,通过坐标法把平面上的点与一对有次序的数对应起来,把平面上的图形和方程对应起来,从而可以用代数的方法来研究几何问题,空间解析几何也是按照类似的方法建立起来的。
 向量的乘法运算:向量a与实数λ的乘积记作aλ,规定aλ是一个向量,它的模|aλ| =|λ||a| ,它的方向当λ>0时与a相同,当λ<0时与a相反。
定理1:设向量a≠0,则向量b平行于a的充分必要条件是:存在唯一的实数λ,使b=λa
向量的乘法运算:向量a与实数λ的乘积记作aλ,规定aλ是一个向量,它的模|aλ| =|λ||a| ,它的方向当λ>0时与a相同,当λ<0时与a相反。
定理1:设向量a≠0,则向量b平行于a的充分必要条件是:存在唯一的实数λ,使b=λa
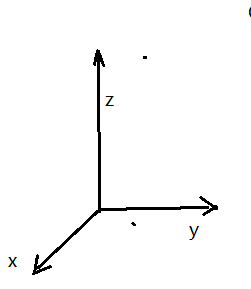
三条坐标轴中的任意两条可以确定一个平面,x与y轴所确定的平面叫xOy面,总共分成了3个平面,空间被分成了8个部分。
r=xi+yj+zk
上式叫做向量r的坐标分解式,xi、yj、zk称为向量r沿三个坐标轴方向的分向量。 显然,只要给定向量r,就确定了点M和三个分向量,进而确定了x、y、z三个有序数;反之给定三个有序数x、y、z,也就确定了向量r和对应点M。
M←→r=xi+yj+zk←→(x,y,z)
有序数x、y、z就是点M在坐标系中的坐标,记作M(x,y,z) 任给向量a,b,那么a=(ax,ay,az),b=(bx,by,bz),依据向量的加减法和乘法规则,易得:
a+b=(ax+bx,ay+by,az+bz)
a-b = (ax-bx,ay-by,az-bz)
λa=(λax,λay,λaz) 注意,记号(x,y,z)即可表示点M,也可表示向量OM,在几何中点与向量是两个不同的概念,须从上下文中认清它究竟表示点还是向量,如果是向量可以进行运算,如果是点,就不能进行运算。
|r|= (x^2+y ^2+ z ^2) ^(1/2)
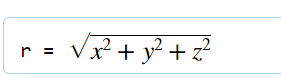
设点A(x1,y1,z1)和点B(x2,y2,z2),则点A与点B间的距离|AB|就是向量AB的模
|AB| = ((x2-x1)^2+(y2-y1) ^2+ (z2-z1) ^2) ^(1/2)
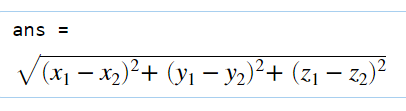
因为根号里开了平方,所以x2-x1和 x1-x2平方后结果相同,这样也容易记。
但要注意,向量AB的坐标是(x2-x1,y2-y1,z2-z1) 在matlab中,单独一个向量a取模,使用函数norm
如果是两个点求距离,也即两点|ab|模,也使用函数norm
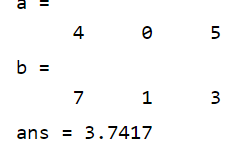
cosα= x/|r| cosβ= y/|r| cosγ = z/|r|
从而(cosα ,cosβ, cosγ) = ( x/|r|, y/|r|, z/|r| ) = (x,y,z)/|r| = r/|r|
cosα ,cosβ, cosγ称为向量r的方向余弦。 例7 已知两点M1(2,2,2^(1/2))和M2(1,3,0),计算向量M1M2的模,方向余弦和方位角。
解:
只有λ为实数时,|aλ| =|λ||a| ,模内的乘法才能拆分出来!!
m1和m2都是向量,绝对不能 |m1m2| ≠ |m1|*|m2|,而是要用公式来算。
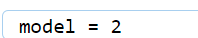
m1m2向量=m2 -m1 = (-1,1,-2^(1/2))
cosα = x/|r| = -1/2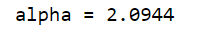
也即2*π/3,与书本上一致。
向量的概念
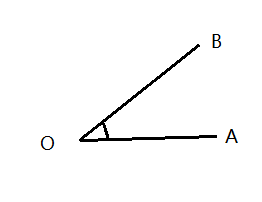
客观世界有这样一类量,它们既有大小,又有方向,例如位移、速度、加速度、力、力矩等,这一类量叫做向量(矢量)。 在数学上,常用一条有方向的线段来表示向量,线段的长度表示向量的大小,线段的方向表示向量的方向。 尽管在实际问题中,有些向量与它的起点有关,有些向量与它的起点无关,为了研究方便,数学上只考虑向量的大小和方向,而不论它的起点,这种向量也叫自由向量。 模:向量的大小叫做向量的模。模为1的向量叫做单位向量,模为0的向量叫做零向量。 夹角:两个向量OA 与OB所形成的角度θ, 0<=θ<=π,如果夹角为0或π,就称向量a与b平行,记作a//b,如果夹角为π/2,就称向量a与b垂直,记作a⊥b
向量的线性运算
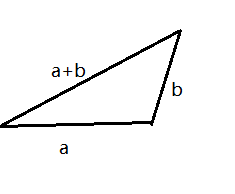
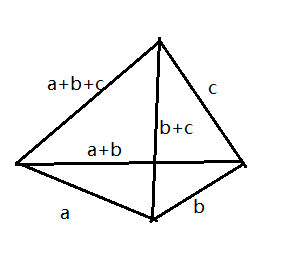
向量的加法运算
 向量的乘法运算:向量a与实数λ的乘积记作aλ,规定aλ是一个向量,它的模|aλ| =|λ||a| ,它的方向当λ>0时与a相同,当λ<0时与a相反。
定理1:设向量a≠0,则向量b平行于a的充分必要条件是:存在唯一的实数λ,使b=λa
向量的乘法运算:向量a与实数λ的乘积记作aλ,规定aλ是一个向量,它的模|aλ| =|λ||a| ,它的方向当λ>0时与a相同,当λ<0时与a相反。
定理1:设向量a≠0,则向量b平行于a的充分必要条件是:存在唯一的实数λ,使b=λa
空间直角坐标系
在空间取一点O和三个两两垂直的单位向量i,j,k,就确定了三条都以O为原点的两两垂直的数轴,形成Oxyz坐标。
三条坐标轴中的任意两条可以确定一个平面,x与y轴所确定的平面叫xOy面,总共分成了3个平面,空间被分成了8个部分。
分解式
任给向量r,有对应点M,于是可证:r=xi+yj+zk
上式叫做向量r的坐标分解式,xi、yj、zk称为向量r沿三个坐标轴方向的分向量。 显然,只要给定向量r,就确定了点M和三个分向量,进而确定了x、y、z三个有序数;反之给定三个有序数x、y、z,也就确定了向量r和对应点M。
M←→r=xi+yj+zk←→(x,y,z)
有序数x、y、z就是点M在坐标系中的坐标,记作M(x,y,z) 任给向量a,b,那么a=(ax,ay,az),b=(bx,by,bz),依据向量的加减法和乘法规则,易得:
a+b=(ax+bx,ay+by,az+bz)
a-b = (ax-bx,ay-by,az-bz)
λa=(λax,λay,λaz) 注意,记号(x,y,z)即可表示点M,也可表示向量OM,在几何中点与向量是两个不同的概念,须从上下文中认清它究竟表示点还是向量,如果是向量可以进行运算,如果是点,就不能进行运算。
向量的模计算
设向量r=(x,y,z),记作r=OM,那么可推出向量的模坐标表达式:|r|= (x^2+y ^2+ z ^2) ^(1/2)
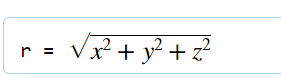
设点A(x1,y1,z1)和点B(x2,y2,z2),则点A与点B间的距离|AB|就是向量AB的模
|AB| = ((x2-x1)^2+(y2-y1) ^2+ (z2-z1) ^2) ^(1/2)
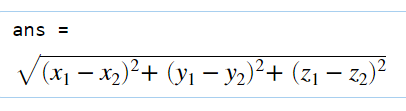
因为根号里开了平方,所以x2-x1和 x1-x2平方后结果相同,这样也容易记。
但要注意,向量AB的坐标是(x2-x1,y2-y1,z2-z1) 在matlab中,单独一个向量a取模,使用函数norm
a=[2,2,1]
norm(a)

如果是两个点求距离,也即两点|ab|模,也使用函数norm
a=[4,0,5]
b=[7,1,3]
norm(b-a)
答案是sqrt(14),即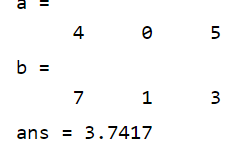
向量的方向角
非零向量r与三条坐标轴的夹角α,β,γ叫做向量r的方向角,易知:cosα= x/|r| cosβ= y/|r| cosγ = z/|r|
从而(cosα ,cosβ, cosγ) = ( x/|r|, y/|r|, z/|r| ) = (x,y,z)/|r| = r/|r|
cosα ,cosβ, cosγ称为向量r的方向余弦。 例7 已知两点M1(2,2,2^(1/2))和M2(1,3,0),计算向量M1M2的模,方向余弦和方位角。
解:
m1=[2,2,2^(1/2)] m2=[1,3,0] model=norm(m1-m2)
|m1|=|m2|=10^(1/2)只有λ为实数时,|aλ| =|λ||a| ,模内的乘法才能拆分出来!!
m1和m2都是向量,绝对不能 |m1m2| ≠ |m1|*|m2|,而是要用公式来算。
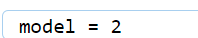
m1m2向量=m2 -m1 = (-1,1,-2^(1/2))
cosα = x/|r| = -1/2
alpha=acos(-1/ans)
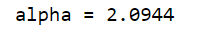
也即2*π/3,与书本上一致。