公式

1. 旋转向量求解旋转矩阵 当刚体在三维空间中运动时,如果已知旋转向量,根据罗德里格斯公式是比较容易求得旋转矩阵的.
罗德里格斯公式如图所示
其中,I 是单位矩阵,n 是旋转向量的单位向量, theta是旋转向量的模长. 2. 旋转矩阵求解旋转向量
如果已知旋转矩阵,求解旋转向量时,theta是比较容易求解的.根据上图,对等式两端取迹便可以得到旋转向量的模长


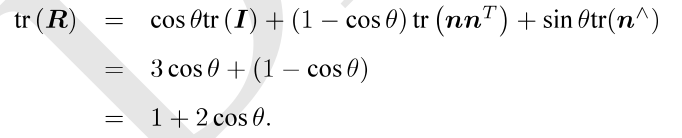
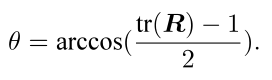
记旋转向量的单位向量为 r(rx, ry, rz) ,通过下图公式便可求解得出 r 向量的反对成矩阵,即可得出 r 向量

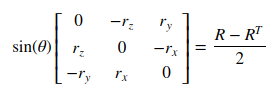
代码

这里用代码简单的求解一下 #include #include using namespace std; using namespace Eigen; int main() { double angle = M_PI / 6.; //X轴向的转角 AngleAxisd angleAxisd(angle, Vector3d(1, 0, 0)); { cout << "根据旋转向量求解旋转矩阵..." << endl; double theta = angleAxisd.angle(); Vector3d n = angleAxisd.axis(); cout<< "theta is " << theta << endl; cout<< "n is " << n << endl; Matrix3d n_hat; n_hat << 0, -n[2], n[1], n[2], 0, -n[0], -n[1], n[0], 0; Matrix3d R_solved = cos(theta) * Matrix3d::Identity() + (1 - cos(theta)) * n * n.transpose() + sin(theta) * n_hat; cout << "R_solved is " << R_solved << endl; } 用OpenCV Documention上的方法求解旋转向量
点击此处搜索Rodrigues { cout<< "根据旋转矩阵求解旋转向量..." << endl; Matrix3d R = angleAxisd.toRotationMatrix(); double theta = acos((R.trace() - 1) * 0.5); //待求的旋转向量的模长 Matrix3d Right = (R - R.transpose()) * 0.5 / sin(theta); Vector3d r; //待求的旋转向量的单位向量 r[0] = (Right(2,1) - Right(1,2))*0.5; r[1] = (Right(0,2) - Right(2,0))*0.5; r[2] = (Right(1,0) - Right(0,1))*0.5; cout<<"angle is "< 用求特征值为1对应的特征向量方法求解旋转向量 { cout<< "根据旋转矩阵求解旋转向量..." << endl; //此处RR和n是相互对应的,用所求的旋转单位向量同n对比验证 Matrix3d RR; RR << -0.036255, 0.978364, -0.203692, 0.998304,0.026169, -0.051994, -0.045539,-0.205232,-0.977653; Vector3d n(-2.100418,-2.167796,0.273330); double theta = acos((RR.trace() - 1) * 0.5); EigenSolver solver(RR); Matrix3cd vectors = solver.eigenvectors(); Vector3cd values = solver.eigenvalues(); cout<<"vectors is "<()*x<