class="markdown_views prism-kimbie-light">
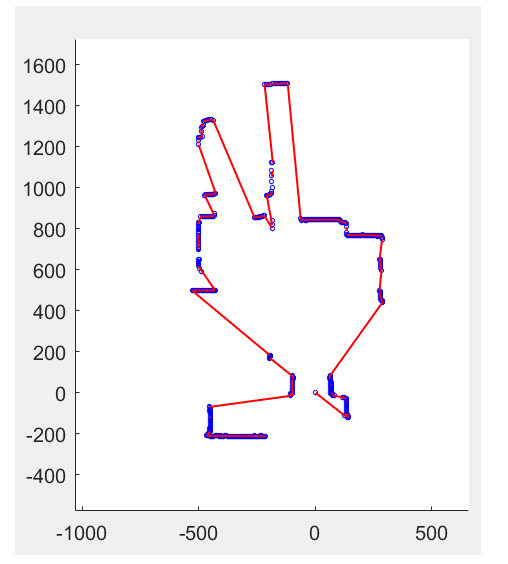
2.回归方法 先聚类,再回归 3.累积、区域生长算法 感觉对噪声数据真的没办法了,窝成一团的点,提取的线十分破碎而且乱…
slam国内外数据库
(牛逼博主连接:https://www.cnblogs.com/yhlx125/p/5609998.html) http://www.ifp.uni-stuttgart.de/ISPRS-EuroSDR/ImageMatching/index.html http://www.robots.ox.ac.uk/NewCollegeData/index.php?n=Main.Downloads#GettingStarted http://asrl.utias.utoronto.ca/datasets/devon-island-rover-navigation/ http://kos.informatik.uni-osnabrueck.de/3Dscans/2D激光扫描匹配方法
1.Beam Model
Beam Model我将它叫做测量光束模型。个人理解,它是一种完全的物理模型,只针对激光发出的测量光束建模。将一次测量误差分解为四个误差。 phhitphhit,测量本身产生的误差,符合高斯分布。 phxxphxx,由于存在运动物体产生的误差。 …2.Likehood field
似然场模型,和测量光束模型相比,考虑了地图的因素。不再是对激光的扫描线物理建模,而是考虑测量到的物体的因素。 似然比模型本身是一个传感器观测模型,之所以可以实现扫描匹配,是通过划分栅格,步进的方式求的最大的Score,将此作为最佳的位姿。for k=1:size(zt,1)
if zt(k,2)>0
d = -grid_dim/2;
else
d = grid_dim/2;
end
phi = pi_to_pi(zt(k,2) + x(3));
if zt(k,1) ~= Z_max
ppx = [x(1),x(1) + zt(k,1)*cos(phi) + d];
ppy = [x(2),x(2) + zt(k,1)*sin(phi) + d];
end_points = [end_points;ppx(2),ppy(2)];
wm = likelihood_field_range_finder_model(X(j,:)',xsensor,...
zt(k,:)',nearest_wall, grid_dim, std_hit,Z_weights,Z_max);
W(j) = W(j) * wm;
else
dist = Z_max + std_hit*randn(1);
ppx = [x(1),x(1) + dist*cos(phi) + d];
ppy = [x(2),x(2) + dist*sin(phi) + d];
missed_points = [missed_points;ppx(2),ppy(2)];
end
set(handle_sensor_ray(k),'XData', ppx, 'YData', ppy)
end
function q = likelihood_field_range_finder_model(X,x_sensor,zt,N,dim,std_hit,Zw,z_max)
% retorna probabilidad de medida range finder :)
% X col, zt col, xsen col
[n,m] = size(N);
% Robot global position and orientation
theta = X(3);
% Beam global angle
theta_sen = zt(2);
phi = pi_to_pi(theta + theta_sen);
%Tranf matrix in case sensor has relative position respecto to robot's CG
rotS = [cos(theta),-sin(theta);sin(theta),cos(theta)];
% Prob. distros parameters
sigmaR = std_hit;
zhit = Zw(1);
zrand = Zw(2);
zmax = Zw(3);
% Actual algo
q = 1;
if zt(1) ~= z_max
% get global pos of end point of measument
xz = X(1:2) + rotS*x_sensor + zt(1)*[cos(phi);
sin(phi)];
xi = floor(xz(1)/dim) + 1;
yi = floor(xz(2)/dim) + 1;
% if end point doesn't lay inside map: unknown
if xi<1 || xi>n || yi<1 || yi>m
q = 1.0/z_max; % all measurements equally likely, uniform in range [0-zmax]
return
end
dist2 = N(xi,yi);
gd = gauss_1D(0,sigmaR,dist2);
q = zhit*gd + zrand/zmax;
end
end
3.Correlation based sensor models相关分析模型
XX提出了一种用相关函数表达马尔科夫过程的扫描匹配方法。 互相关方法Cross-Correlation,另外相关分析在进行匹配时也可以应用,比如对角度直方图进行互相关分析,计算变换矩阵。 参考文献:A Map Based On Laser scans without geometric interpretation circular Cross-Correlation的Matlab实现% Computes the circular cross-correlation between two sequences
%
% a,b the two sequences
% normalize if true, normalize in [0,1]
%
function c = circularCrossCorrelation(a,b,normalize)
for k=1:length(a)
c(k)=a*b';
b=[b(end),b(1:end-1)]; % circular shift
end
if normalize
minimum = min(c);
maximum = max(c);
c = (c - minimum) / (maximum-minimum);
end
4.MCL
蒙特卡洛方法
5.AngleHistogram
角度直方图
6.ICP/PLICP/MBICP/IDL
属于ICP系列,经典ICP方法,点到线距离ICP,
7.NDT
正态分布变换
8.pIC
结合概率的方法
9.线特征
目前应用线段进行匹配的试验始终不理想:因为线对应容易产生错误,而且累积误差似乎也很明显!
2D激光线特征提取
Nguyen, V., et al. (2007).“A comparison of line extraction algorithms using 2D range data for indoor mobile robotics.” Autonomous Robots 23(2): 97-111. 论文提出了6中从二维激光扫描数据中提取线段的方法 1.分割合并算法
2.回归方法 先聚类,再回归 3.累积、区域生长算法 感觉对噪声数据真的没办法了,窝成一团的点,提取的线十分破碎而且乱…
function [ lineSegCoord ] = extractLineSegment( model,normals,intervalPts,normalDelta,dThreshold)
%EXTRACTLINESEGMENT Summary of this function goes here
% Detailed explanation goes here
if (nargin == 0) || isempty(model)
lineSegCoord = [];
return;
end;
ns = createns(model','NSMethod','kdtree')
pts=size(model,2);
if (nargin == 3)
normalDelta=0.9;
dThreshold=0.5;
end
if isempty(normals)
normals=zeros(2,pts);
for nor=1:pts
[idx, dist] = knnsearch(ns,model(:,nor)','k',2);
data=model(:,idx);
men=mean(data,2);
rep= repmat(men,1,size(data,2));
data = data - rep;
% Compute the MxM covariance matrix A
A = cov(data');
% Compute the eigenvector of A
[V, LAMBDA] = eig(A);
% Find the eigenvector corresponding to the minimum eigenvalue in A
% This should always be the first column, but check just in case
[~,idx] = min(diag(LAMBDA));
% Normalize
V = V(:,idx)./norm(V(:,idx));
%定向
normals(:,nor)=V;
end
end
lineSeg=[1;1];
newLineIdx=1;
for j=2:pts-1
current=model(:,j);
pre=model(:,j-1);
next=model(:,j+1);
curNormal=normals(:,j);
preNormal=normals(:,j-1);
nextNormal=normals(:,j+1);
[d,vPt]=Dist2D_Point_to_Line(current,pre,next);
dis=norm(current-pre);
delta=dot(curNormal,preNormal)/(norm(curNormal)*norm(preNormal));
if(delta>normalDelta&& d intervalPts)
try
pts= model(:,(from:to));
coef1 = polyfit(pts(1,:),pts(2,:),1);
k2 = coef1(1);
b2 = coef1(2);
coef2 = robustfit(pts(1,:),pts(2,:),'welsch');
k2 = coef2(2);
b2 = coef2(1);
ML = true;
catch
ML = false;
end;
[D,fPb]= Dist2D_Point_to_Line(model(:,from),[0 b2]',[1 k2+b2]');
[D,tPb]= Dist2D_Point_to_Line(model(:,to),[0 b2]',[1 k2+b2]');
interval=abs(model(1,from) -model(1,to));
if(interval>0.05)
x = linspace(fPb(1) ,tPb(1), 5);
if ML
y_ML = k2*x +b2;
lineSegCoord=[lineSegCoord [fPb(1) fPb(2) tPb(1) tPb(2)]'];
plot(x, y_ML, 'b-', 'LineWidth', 1);
end;
else
y = linspace(fPb(2) ,tPb(2), 5);
if ML
x_ML =(y-b2)/k2;
lineSegCoord=[lineSegCoord [fPb(1) fPb(2) tPb(1) tPb(2)]'];
plot(x_ML, y, 'b-', 'LineWidth', 1);
end;
end;
% try
% tmpPts= model(:,(from:to));
% Theta_ML = estimate_line_ML(tmpPts,[], sigma, 0);
% ML = true;
% catch
% % probably the optimization toolbox is not installed
% ML = false;
% end;
% interval=abs(model(1,from) -model(1,to));
% if(interval>10)
% x = linspace(model(1,from) ,model(1,to), 5);
% if ML
% y_ML = -Theta_ML(1)/Theta_ML(2)*x - Theta_ML(3)/Theta_ML(2);
% lineSegCoord=[lineSegCoord [x(1) y_ML(1) x(5) y_ML(5)]'];
% plot(x, y_ML, 'b-', 'LineWidth', 1);
% end;
% else
% y = linspace(model(2,from) ,model(2,to), 5);
% if ML
% x_ML = -Theta_ML(2)/Theta_ML(1)*y - Theta_ML(3)/Theta_ML(1);
% lineSegCoord=[lineSegCoord [x_ML(1) y(1) x_ML(5) y(5)]'];
% plot(x_ML, y, 'b-', 'LineWidth', 1);
% end;
% end;
end
end
end
4.Ransac方法
5.霍夫变换方法
6.EM方法