概要 　　本篇接上一篇继续介绍网格生成算法，同时不少内容继承自上篇。上篇介绍了经典的三维图像网格生成算法MarchingCubes，并且基于其思想和三角形表实现了对样例数据的网格构建。本篇继续探讨网格生成算法，并且在MC的基础上进行进一步的简化和改进，形成Simple Marching Cubes（简称SMC算法）。本篇主要介绍SMC算法的思路以及与MC算法的对比。同时也介绍如何在MC三角形表的基础上生成SMC三角形表。 SMC算法原理 　　MC算法的思想之一是构造在实点和虚点之间等值面来拟合用于表示边界的曲面。在上篇中也提到在包含有实点和虚点的边界体元内，通过在体元边上计算插值点来构造三角片。实际上，由于每一个体元相对三维图像都是一个足够小的局部，所以其中的每一片三角形的顶点位置在所插值的边上进行适当的移动也不会对Mesh的整体形状有较大的影响。也就是说，无论插值点的计算方式是取中点，取端点亦或是取体素值加权后的点，最后的边界面形状也不会有太大的改变。C. Montani在Discretized Marching Cubes这篇文章中对这种近似也有过解释，在他的文章中，他对MC的改进使用的插值点总是体元边中点，这样就增加了三角形的规则度，便于后续的简化。这里对这篇文章的优化方法不做更多的讨论，总之要说明的问题就是，MC算法的等值面在一个体元的局部内移动，对实际曲面的整体形状影响不大。如下图： 　　实点假如像素值为240，虚点像素值为0则值为120的等值线是正好处在中间，而不同值的等值面也都处于边界体元的区域之内。值为240和0的等值线分别是可能的最靠里和最靠外的等值线。这些等值线都能表征虚实点的边界。 　　左图画出了MC算法的边界线，而右图是边界线移到贴近实点处的边界线。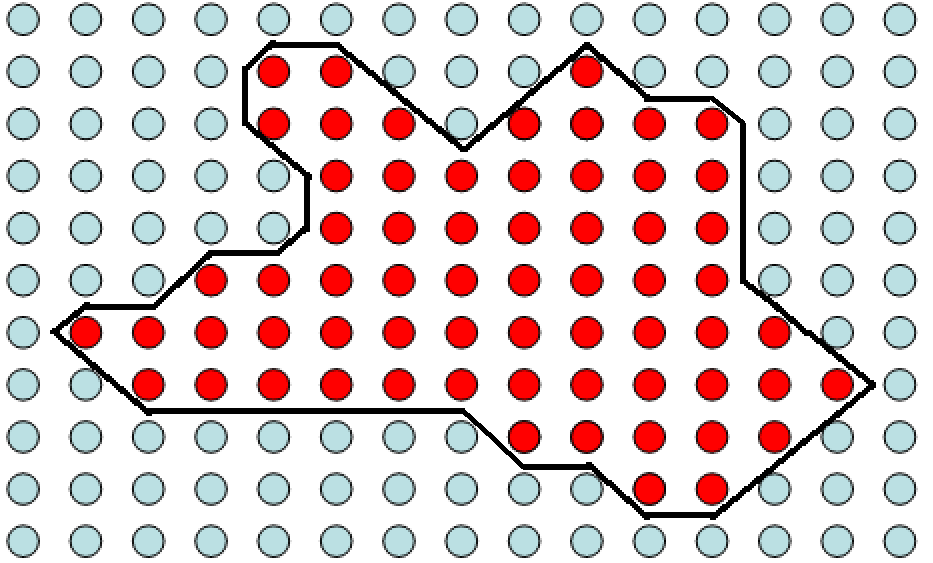   MC算法的边界线   边界线移到贴近实点处的边界线 　　我们可以看出，两条线无论是前者还是后者。实际上都能够作为表征内容边界的包络线。而后者在结构上更加简洁。实际上SMC算法就是利用这一点，通过求取更加简单的包络面，使用比MC算法规模更小的Mesh来表示相同的曲面。通过以上的分析可知，想要达到这个目的，只需求出类似文中的穿过实点或虚点的那一层等值面即可。下文为了方便叙述，穿过实点的等值面（如上文中的240等值面）被称作“瘦包络面”。穿过虚点的等值面（如上文中的0等值面）就称作“胖包络面”。而介于这两者之间的所有等值面都称作“一般等值面”。 　　经典MC算法有15种基本构型，其中14种包含三角片，下文的表罗列了这14种情况所对应的三角片以及转化为胖瘦包络面后的三角片情况。 编号 一般等值面三角片 描述 对应的瘦包络面三角片 描述 对应的胖包络面三角片 描述 1 实点数:1 三角形数：1   三角形数：0 退化三角形：1 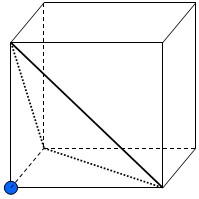三角形数：1 退化三角形：1 2   实点数:1 三角形数：2   三角形数：0 退化三角形：2   三角形数：2 退化三角形：0 3 实点数:2 三角形数：2     三角形数：0 退化三角形：2   三角形数：2 退化三角形：0 4 实点数:2 三角形数：2     三角形数：0 退化三角形：2   三角形数：2 退化三角形：0 5 实点数:3 三角形数：3     三角形数：1 退化三角形：2   三角形数：2 退化三角形：1 6 实点数:3 三角形数：3 （这种配置连接方 式不止这一种）  三角形数：0 退化三角形：3     三角形数：3 退化三角形：0 7 实点数:3 三角形数：3   三角形数：0 退化三角形：3   三角形数：3 退化三角形：0   8   实点数:4 三角形数：2   三角形数：2 退化三角形：0   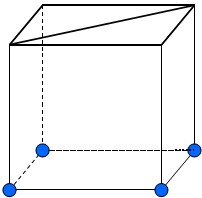三角形数：2 退化三角形：0 9 实点数:4 三角形数：4   三角形数：1 退化三角形：3   三角形数：1 退化三角形：3   10   实点数:4 三角形数：4   三角形数：0 退化三角形：4   三角形数：4 退化三角形：0 11 实点数:4 三角形数：4   三角形数：2 退化三角形：2     三角形数：2 退化三角形：2 12   实点数:4 三角形数：4 三角形数：1 退化三角形：3   三角形数：3 退化三角形：1   13 实点数:4 三角形数：4   三角形数：0 退化三角形：4   三角形数：4 退化三角形：0   14 实点数:4 三角形数：4     三角形数：2 退化三角形：2   三角形数：2 退化三角形：2 　　从表中看出，MC算法14种包含三角片的构型在进行插值点移动后，部分构型中三角形发生退化，即有顶点出现重合从而不再是一个可见的三角形。同时在移动三角形顶点位置之后，所有三角形的顶点只可能是体元的8个体素点之一，也就是说，三角形可以不再像MC算法中那样由各边的插值点构成，而是可以由体素顶点构成。所以若想使用简化后的构型来构建三角网格，就需要对简化后的体元重新建立体元配置到三角形信息的三角形表。之后，就能使用这个新的三角形表来抽取三角形，最终拼接成完整的Mesh。 　　综上所述，SMC算法就是采用与MC算法不同的三角形表去构建Mesh，而它的三角形表是由MC算法的三角形表进行转化而成的。 如何构建新的三角形表 　　参考MC三角形表的二维数组的形式，SMC三角形表也是256*16大小的二维数组，由于SMC算法有胖和瘦两种包络面，所以分别对应两个二维数组。这里的代码使用C#语言，对一个Cube按原MC算法计算三角形片，同时计算插值点位置时采用端点值，最后检查三角形是否退化来发现SMC算法最后可见的三角形片，并记录在二维数组中。 class SMCTableGenerator { public int[,] TableFat = new int[256, 16];// table to be filled public void InitTable() { for (int i = 0; i < 255; i++) { List tlist = GetTriangle((byte)i);//find triangles in cube config i int index = 0; for (int j = 0; j < tlist.Count; j++) { Triangle t = tlist[i]; int index1 = t.P0Index; int index2 = t.P1Index; int index3 = t.P2Index; TableFat[i, index] = index1; TableFat[i, index + 1] = index2; TableFat[i, index + 2] = index3; index += 3; }//fill table with triangle data } } private bool IsDegenerated(Triangle originalTriangle) { return originalTriangle.P0Index == originalTriangle.P1Index || originalTriangle.P1Index == originalTriangle.P2Index || originalTriangle.P2Index == originalTriangle.P0Index; }//check if the triangle is degenerated private List GetTriangle(byte cubeConfig) { List list = new List(); if (MCTable.TriTable[cubeConfig, 0] != -1) { int index = 0; while (MCTable.TriTable[cubeConfig, index] != -1) { int ei1 = MCTable.TriTable[cubeConfig, index]; int ei2 = MCTable.TriTable[cubeConfig, index + 1]; int ei3 = MCTable.TriTable[cubeConfig, index + 2]; //find edge indices which is intersected int e0p0 = Cube.EdgeIndexToEdgeVertexIndex[ei1,0]; int e0p1 = Cube.EdgeIndexToEdgeVertexIndex[ei1,1]; int e1p0 = Cube.EdgeIndexToEdgeVertexIndex[ei2,0]; int e1p1 = Cube.EdgeIndexToEdgeVertexIndex[ei2,1]; int e2p0 = Cube.EdgeIndexToEdgeVertexIndex[ei3,0]; int e2p1 = Cube.EdgeIndexToEdgeVertexIndex[ei3,1]; //find out their vertices bool creatFatTable = true;//if need thin table just change this to false; int e0pm = GetNewIntersetVertexIndex(cubeConfig, e0p0, e0p1, creatFatTable); int e1pm = GetNewIntersetVertexIndex(cubeConfig, e1p0, e1p1, creatFatTable); int e2pm = GetNewIntersetVertexIndex(cubeConfig, e2p0, e2p1, creatFatTable); //get the vertex to build the triangle Triangle t = new Triangle(e0pm, e1pm, e2pm); if (!IsDegenerated(t)) { list.Add(t); }//check if the triangle is degenerated index += 3; }//for each triangle } return list; }//get triangles from mc table by cube config private int GetNewIntersetVertexIndex(byte cubeConfig,int v0,int v1,bool isfat) { if (IsInside(cubeConfig, v0) && !IsInside(cubeConfig, v1)) { if (isfat) return v1; else return v0; } else if (!IsInside(cubeConfig, v0) && IsInside(cubeConfig, v1)) { if (isfat) return v0; else return v1; } else { throw new Exception(); } }//decide which vertex chosed to be the interseted one private bool IsInside(byte p, int ep0) { return (p & Cube.PointIndexToFlag[ep0]) != 0; }//check if the vertex is white }//generator smc table from classic marching cubes tables 　　上述代码初始化TableFat这个二维数组，将其填充为构建胖包络面的三角形表，为了以后能重复利用，输出这个三角形表为文本形式的C#代码，最后形成了这样的表。 #region TableFat public static int[,] TableFat = new int[256, 16] { {-1,-1,-1,-1,-1,-1,-1,-1,-1,-1,-1,-1,-1,-1,-1,-1}, {1,4,3,-1,-1,-1,-1,-1,-1,-1,-1,-1,-1,-1,-1,-1}, {0,2,5,-1,-1,-1,-1,-1,-1,-1,-1,-1,-1,-1,-1,-1}, {2,4,3,5,4,2,-1,-1,-1,-1,-1,-1,-1,-1,-1,-1}, {1,3,6,-1,-1,-1,-1,-1,-1,-1,-1,-1,-1,-1,-1,-1}, {1,4,3,1,3,6,-1,-1,-1,-1,-1,-1,-1,-1,-1,-1}, {5,3,6,0,3,5,-1,-1,-1,-1,-1,-1,-1,-1,-1,-1}, {3,6,4,6,5,4,-1,-1,-1,-1,-1,-1,-1,-1,-1,-1}, {0,7,2,-1,-1,-1,-1,-1,-1,-1,-1,-1,-1,-1,-1,-1}, {1,7,2,4,7,1,-1,-1,-1,-1,-1,-1,-1,-1,-1,-1}, {2,5,0,2,0,7,-1,-1,-1,-1,-1,-1,-1,-1,-1,-1}, {2,5,7,5,4,7,-1,-1,-1,-1,-1,-1,-1,-1,-1,-1}, {0,6,1,7,6,0,-1,-1,-1,-1,-1,-1,-1,-1,-1,-1}, {1,4,6,4,7,6,-1,-1,-1,-1,-1,-1,-1,-1,-1,-1}, {0,7,5,7,6,5,-1,-1,-1,-1,-1,-1,-1,-1,-1,-1}, {5,4,6,6,4,7,-1,-1,-1,-1,-1,-1,-1,-1,-1,-1}, {5,7,0,-1,-1,-1,-1,-1,-1,-1,-1,-1,-1,-1,-1,-1}, {5,3,1,7,3,5,-1,-1,-1,-1,-1,-1,-1,-1,-1,-1}, {0,2,5,0,5,7,-1,-1,-1,-1,-1,-1,-1,-1,-1,-1}, {5,7,2,7,3,2,-1,-1,-1,-1,-1,-1,-1,-1,-1,-1}, {1,3,6,0,5,7,-1,-1,-1,-1,-1,-1,-1,-1,-1,-1}, {3,5,7,3,1,5,1,3,6,-1,-1,-1,-1,-1,-1,-1}, {5,3,6,5,0,3,0,5,7,-1,-1,-1,-1,-1,-1,-1}, {3,6,5,3,5,7,-1,-1,-1,-1,-1,-1,-1,-1,-1,-1}, {0,5,7,0,7,2,-1,-1,-1,-1,-1,-1,-1,-1,-1,-1}, {7,2,5,2,1,5,-1,-1,-1,-1,-1,-1,-1,-1,-1,-1}, {5,0,2,0,5,7,2,0,7,-1,-1,-1,-1,-1,-1,-1}, {5,7,2,-1,-1,-1,-1,-1,-1,-1,-1,-1,-1,-1,-1,-1}, {0,6,1,0,7,6,7,0,5,-1,-1,-1,-1,-1,-1,-1}, {1,7,