系统分区
映射
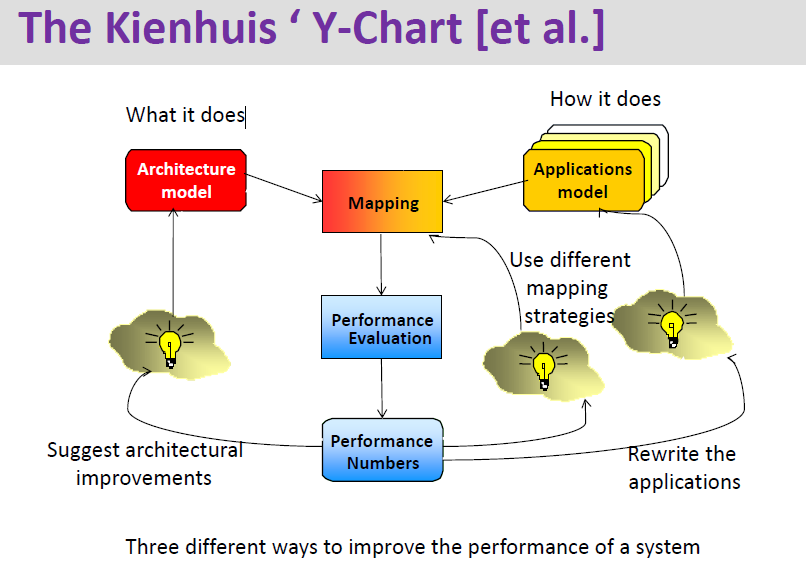
概念
从上图我们可以看到一共有三种方法去提高系统的性能:架构提高,重写应用,使用不同的策略。映射(mapping)就是把行为级转换为结构和执行。
最后综合的时候,是包括分区和映射两个部分。其中分区就是分配(选择模块)和绑定(把一些函数给部件);映射就是包括绑定和调度(执行顺序)。最后综合的结果就会被执行。其实就是我们选择什么器件,它要执行什么函数,执行顺序是什么。就这样的过程。
抽象层次
- 低层次:RTL或者网表。将数字电路映射到具体设备上(FPGA,ASIC);系统参数(比如面积,延时)相对容易去决定。
- 高层次:系统层次。选择最优设计(比如空间大小);难以了解或者决定的系统参数(通过一些模型,分析,模拟,原型来实现)。
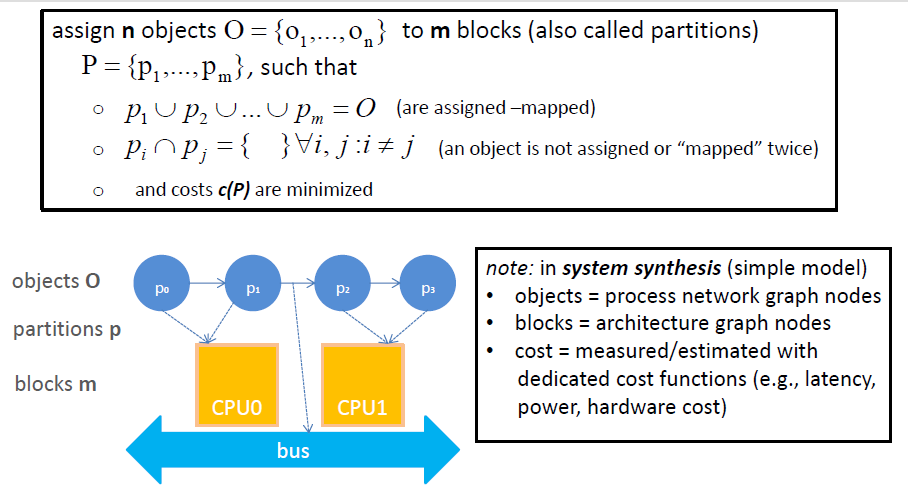
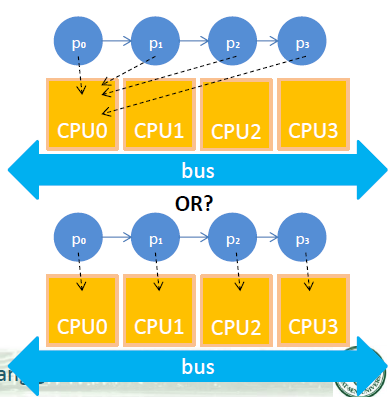 就上图其实就是表现了映射关系:N对一和一对一。
就上图其实就是表现了映射关系:N对一和一对一。 在这里我们要考虑的问题有:成本:用多少处理器呢?延时:就是频率,当然是越快越好。能以最短的时间解决问题。但是这两个东西是矛盾的,我们要使得成本提高,延时就降低;反之亦然。我们设计的时候就需要提出一些约束才能使得设计求出最优解。 用下图展示一下:
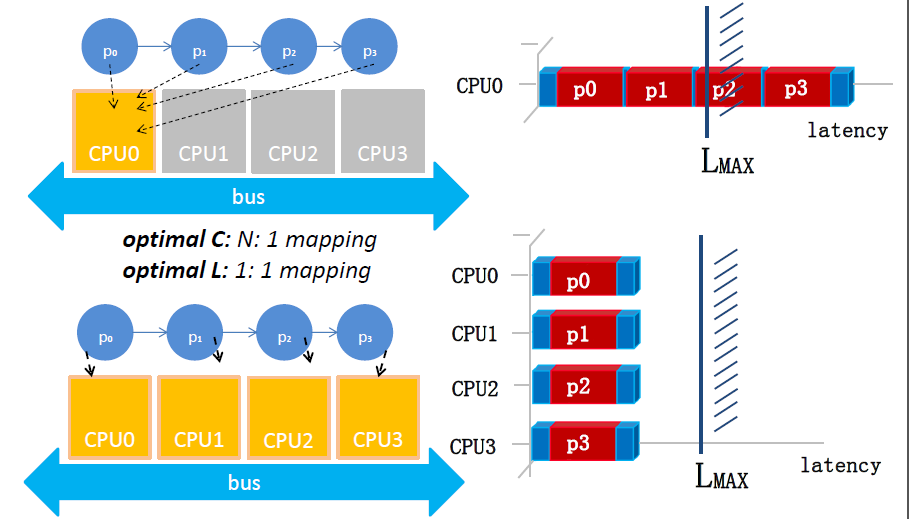 假设任务都是一样长的,那么我们发现若只用一个cpu,延时已经超过了我们的要求,使用四核得话可以很好地满足我们的要求。
假设任务都是一样长的,那么我们发现若只用一个cpu,延时已经超过了我们的要求,使用四核得话可以很好地满足我们的要求。
成本函数
对于cost function,我们先定义一些变量。system cost C [$],latency L[sec],power consumption P[W]。接着我们对这三个都有一个估计函数,然后我们可以得到的是: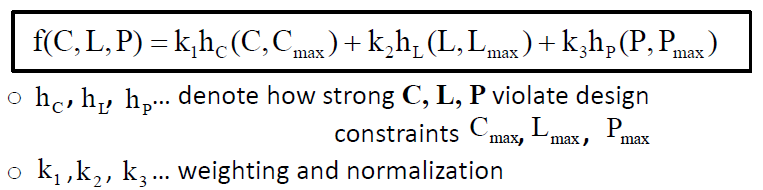 在这里,我们可以看到对于这个函数我们对于不同的变量已经做了加权,我们需要的是进行最优化问题。
所以就有了一个问题:
在这里,我们可以看到对于这个函数我们对于不同的变量已经做了加权,我们需要的是进行最优化问题。
所以就有了一个问题:
分区方法
确定的方法(exat method)
枚举法
枚举法就是一个一个列出来,然后找出最好的那个。这就是枚举,这样的枚举对于很大数据的时候就很让人心塞啊!ILP(integer linear programs)
ILP是进行多目标优化的算法,这个算法非常重要。接下来会详细介绍这个算法。 在这里说到ILP的组成:开销函数和约束函数。我们的目标就是在满足约束的条件下最小化开销函数。
接下来我们来说一下0/1 IP问题,就是加权系数为0或者1。
举一个例子比什么都好:
在这里说到ILP的组成:开销函数和约束函数。我们的目标就是在满足约束的条件下最小化开销函数。
接下来我们来说一下0/1 IP问题,就是加权系数为0或者1。
举一个例子比什么都好:
 我们再把这个问题转化为一般问题:
我们再把这个问题转化为一般问题:
 下面在举一个例子:
下面在举一个例子:
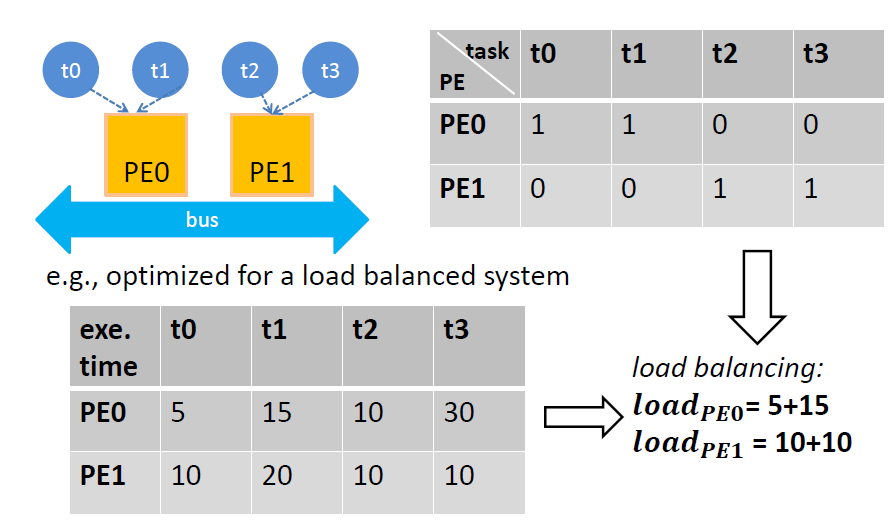 使用ILP的好处是可以增加约束,现在很多都在用这种方法。
就上面那个实际问题,那么我们怎么列出代码呢?
使用ILP的好处是可以增加约束,现在很多都在用这种方法。
就上面那个实际问题,那么我们怎么列出代码呢?
syms x1 x2 x3 x4;
a = [5 15 10 30 10 20 10 10];
x = [x1;x2;x3;x4;(1-x1);(1-x2);(1-x3);(1-x4)];
f = a*x;
lb = zeros(4,1);
ub = ones(4,1);
fx = [-5;-5;0;20];
A = [1 1 1 1];
b = 2;
Aeq = [1 1 1 1];
beq = 2;
intcon = 3;
schedule = intlinprog(fx,intcon,A,b,Aeq,beq,lb,ub)
disp('最后可以得到最短时间为');
subs(f, [x1 x2 x3 x4] ,[ schedule(1) schedule(2) schedule(3) schedule(4)])
 采用这种方法还可以进行最大化问题:
采用这种方法还可以进行最大化问题:
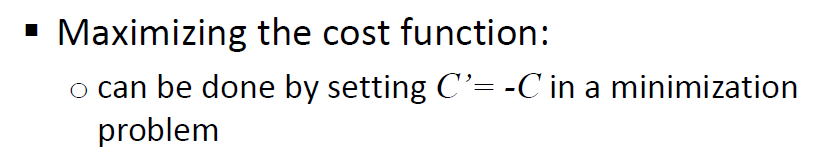 整数规划是一个完全NP问题。在实践中,运行时间可能指数增长,但是几千个变量也可以被解决。IP模型可以作为heuristic optimization method的起点。
接下来举一个例子你就对于ILP更加了解了。
整数规划是一个完全NP问题。在实践中,运行时间可能指数增长,但是几千个变量也可以被解决。IP模型可以作为heuristic optimization method的起点。
接下来举一个例子你就对于ILP更加了解了。
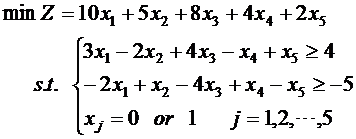 matlab代码如下:
matlab代码如下:
f = [10 5 8 4 2];
intcon = 1:5;
A = [-3,2,-4,1,-1;2,-1,4,-1,1];
b = [-4;5];
Aeq = [];
beq = [];
lb = zeros(5,1);
ub = ones(5,1);
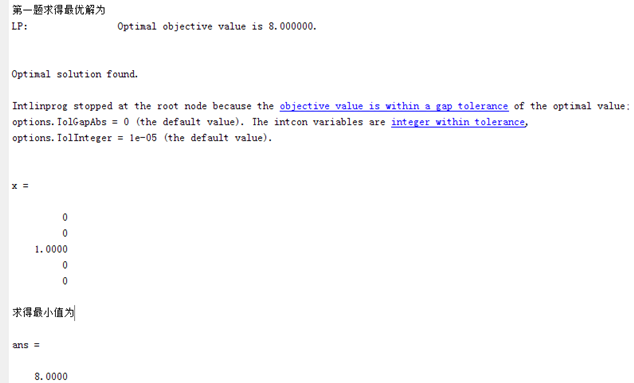
disp('第一题求得最优解为');
x = intlinprog(f,intcon,A,b,Aeq,beq,lb,ub)
disp('求得最小值为');
f*x
运行结果为: