DSP

FFT算法的完整DSP实现

2019-07-13 09:44发布生成海报

站内文章 / DSP

16287 0

傅里叶变换或者FFT的理论参考：[1] http://www.dspguide.com/ch12/2.htm The Scientist and Engineer's Guide to Digital Signal Processing, By Steven W. Smith, Ph.D.[2] http://blog.csdn.net/v_JULY_v/article/details/6196862，可当作[1]的中文参考[3] 任意一本数字信号处理教材，上面都有详细的推导DCT求解转换为FFT求解的过程[4] TI文档：基于TMS320C64x+DSP的FFT实现。使用baidu/google可以搜索到。另外，FFT的开源代码可参考：[1] FFTW: http://www.fftw.org/ 最快，最好的开源FFT。[2] FFTReal: http://ldesoras.free.fr/prod.html#src_fftreal 轻量级FFT算法实现[3] KISS FFT: http://sourceforge.net/projects/kissfft/ 简单易用的FFT的C语言实现

1. 有关FFT理论的一点小小解释

关于FFT这里只想提到两点：（1）DFT变换对的表达式（必须记住）

—— 称旋转因子
（2）FFT用途——目标只有一个，加速DFT的计算效率。DFT计算X(k)需要N^2次复数乘法和N(N-1)次复数加法；FFT将N^2的计算量降为

。
“FFT其实是很难的东西，即使常年在这个领域下打拼的科学家也未必能很好的写出FFT的算法。”——摘自参考上面提供的参考文献[1]因此，我们不必太过纠结于细节，当明白FFT理论后，将已有的算法挪过来用就OK了，不必为闭着教材写不出FFT而郁闷不堪。
FFT的BASIC程序伪代码如下：

IFFT的BASIC程序伪代码如下（IFFT通过调用FFT计算）：

FFT算法的流程图如下图，总结为3过程3循环：（1）3过程：单点时域分解（倒位序过程） + 单点时域计算单点频谱 + 频域合成（2）3循环：外循环——分解次数，中循环——sub-DFT运算，内循环——2点蝶形算法

分解过程或者说倒位序的获得参考下图理解：

2. FFT的DSP实现

下面为本人使用C语言实现的FFT及IFFT算法实例，能计算任意以2为对数底的采样点数的FFT，算法参考上面给的流程图。

/*
 * zx_fft.h
 *
 *  Created on: 2013-8-5
 *      Author: monkeyzx
 */

#ifndef ZX_FFT_H_
#define ZX_FFT_H_

typedef float          FFT_TYPE;

#ifndef PI
#define PI             (3.14159265f)
#endif

typedef struct complex_st {
	FFT_TYPE real;
	FFT_TYPE img;
} complex;

int fft(complex *x, int N);
int ifft(complex *x, int N);
void zx_fft(void);

#endif /* ZX_FFT_H_ */

/*
 * zx_fft.c
 *
 * Implementation of Fast Fourier Transform(FFT)
 * and reversal Fast Fourier Transform(IFFT)
 *
 *  Created on: 2013-8-5
 *      Author: monkeyzx
 */

#include "zx_fft.h"
#include 
#include 

/*
 * Bit Reverse
 * === Input ===
 * x : complex numbers
 * n : nodes of FFT. @N should be power of 2, that is 2^(*)
 * l : count by bit of binary format, @l=CEIL{log2(n)}
 * === Output ===
 * r : results after reversed.
 * Note: I use a local variable @temp that result @r can be set
 * to @x and won't overlap.
 */
static void BitReverse(complex *x, complex *r, int n, int l)
{
	int i = 0;
	int j = 0;
	short stk = 0;
	static complex *temp = 0;

	temp = (complex *)malloc(sizeof(complex) * n);
	if (!temp) {
		return;
	}

	for(i=0; i>(j++)) & 0x01;
			if(j
程序在TMS320C6713上实验，主函数中调用zx_fft()函数即可。FFT的采样点数为128，输入信号的实数域为正弦信号，虚数域为0，数据精度定义FFT_TYPE为float类型，MakeInput和MakeOutput函数分别用于产生输入数据INPUT和输出数据OUTPUT的函数，便于使用CCS 的Graph功能绘制波形图。这里调试时使用CCS v5中的Tools -> Graph功能得到下面的波形图（怎么用自己琢磨，不会的使用CCS 的Help）。输入波形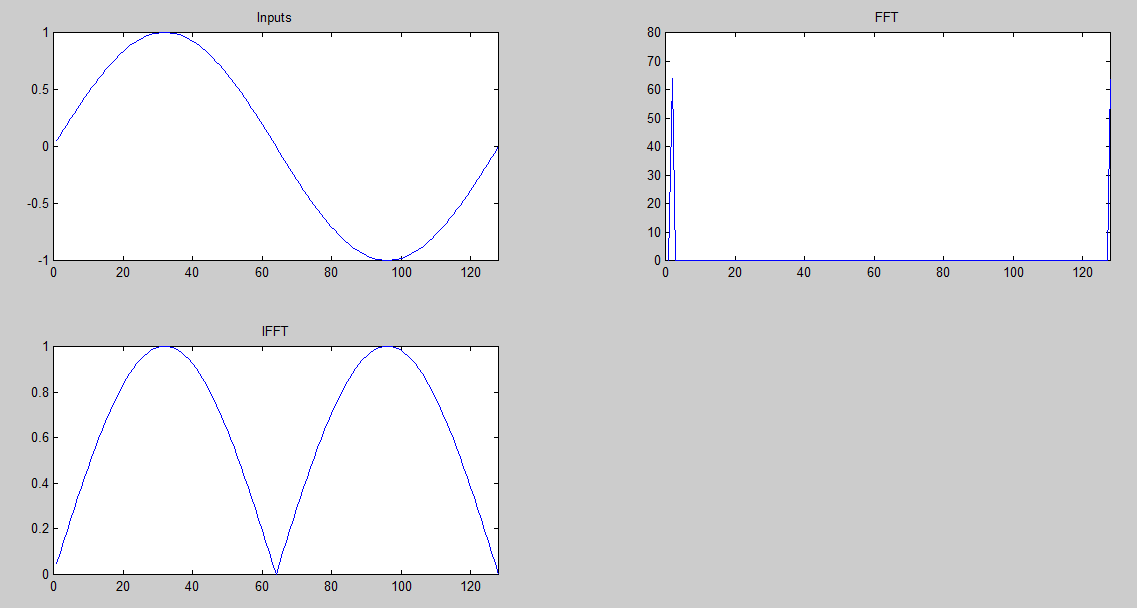
输入信号的频域幅值表示
FFT运算结果

对FFT运算结果逆变换(IFFT)


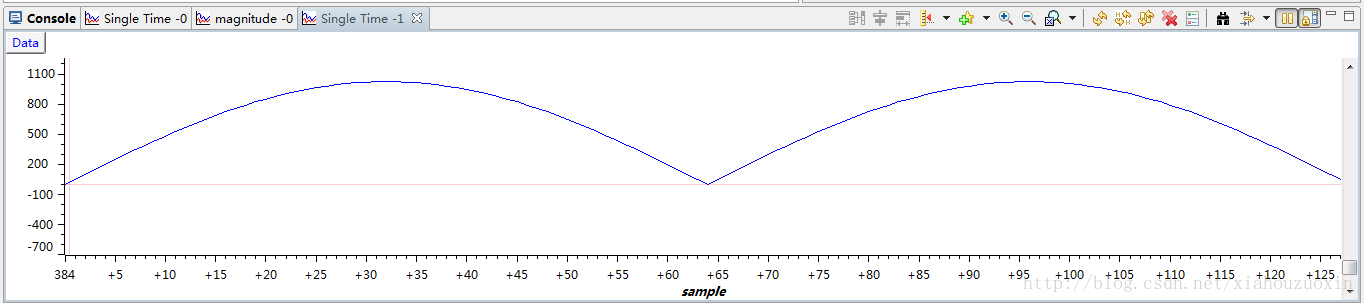
如何检验运算结果是否正确呢？有几种方法：（1）使用matlab验证，下面为相同情况的matlab图形验证代码SAMPLE_NODES = 128;
i = 1:SAMPLE_NODES;
x = sin(pi*2*i / SAMPLE_NODES);

subplot(2,2,1); plot(x);title('Inputs');
axis([0 128 -1 1]);

y = fft(x, SAMPLE_NODES);
subplot(2,2,2); plot(abs(y));title('FFT');
axis([0 128 0 80]);

z = ifft(y, SAMPLE_NODES);
subplot(2,2,3); plot(abs(z));title('IFFT');
axis([0 128 0 1]);

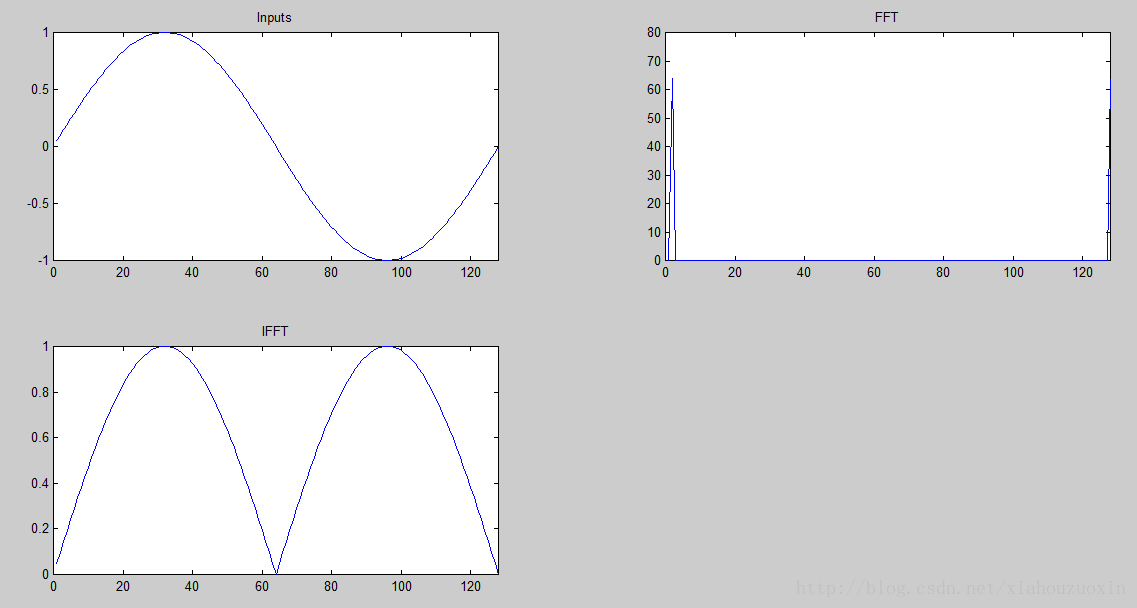
（2）使用IFFT验证：输入信号的FFT获得的信号再IFFT，则的到的信号与原信号相同可能大家发现输入信号上面的最后IFFT的信号似乎不同，这是因为FFT和IFFT存在精度截断误差（也叫数据截断噪声，意思就是说，我们使用的float数据类型数据位数有限，没法完全保留原始信号的信息）。因此，IFFT之后是复数（数据截断噪声引入了虚数域，只不过值很小），所以在绘图时使用了计算幅值的方法，C代码中：OUTPUT[i] = sqrt(x[i].real*x[i].real + x[i].img*x[i].img)*1024;matlab代码中：subplot(2,2,3); plot(abs(z));title('IFFT');所以IFFT的结果将sin函数的负y轴数据翻到了正y轴。另外，在CCS v5的图形中我们将显示信号的幅度放大了1024倍便于观察，而matlab中没有放大。
=================
更正 更正 。。。=================上面程序中的BitReverse函数由于使用了malloc函数，当要分配的n比较大时，在DSP上运行会出现一定的问题，因此改用伪代码中提供的倒位序方法更可靠。修正后的完整FFT代码文件粘贴如下，在实际的DSP项目中测试通过，可直接拷贝复用。/*
 * zx_fft.h
 *
 *  Created on: 2013-8-5
 *      Author: monkeyzx
 */

#ifndef _ZX_FFT_H
#define _ZX_FFT_H

#include "../Headers/Global.h"

#define TYPE_FFT_E     float    /* Type is the same with COMPLEX member */     

#ifndef PI
#define PI             (3.14159265f)
#endif

typedef COMPLEX TYPE_FFT;  /* Define COMPLEX in Config.h */

extern int fft(TYPE_FFT *x, int N);
extern int ifft(TYPE_FFT *x, int N);

#endif /* ZX_FFT_H_ */
/*
 * zx_fft.c
 *
 * Implementation of Fast Fourier Transform(FFT)
 * and reversal Fast Fourier Transform(IFFT)
 * 
 *  Created on: 2013-8-5
 *      Author: monkeyzx
 *
 * TEST OK 2014.01.14
 * == 2014.01.14
 *   Replace @BitReverse(x,x,N,M) by refrence to 
 *   
 */

#include "zx_fft.h"

/*
 * FFT Algorithm
 * === Inputs ===
 * x : complex numbers
 * N : nodes of FFT. @N should be power of 2, that is 2^(*)
 * === Output ===
 * the @x contains the result of FFT algorithm, so the original data
 * in @x is destroyed, please store them before using FFT.
 */
int fft(TYPE_FFT *x, int N)
{
	int i,j,l,k,ip;
	static int M = 0;
	static int le,le2;
	static TYPE_FFT_E sR,sI,tR,tI,uR,uI;

	M = (int)(log(N) / log(2));

	/*
	 * bit reversal sorting
	 */
	l = N / 2;
	j = l;
	//BitReverse(x,x,N,M);
    for (i=1; i<=N-2; i++) {
        if (i < j) {
            tR = x[j].real;
			tI = x[j].imag;
            x[j].real = x[i].real;
			x[j].imag = x[i].imag;
            x[i].real = tR;
			x[i].imag = tI;
		}
		k = l;
		while (k <= j) {
            j = j - k;
			k = k / 2;
		}
		j = j + k;
	}

	/*
	 * For Loops
	 */
	for (l=1; l<=M; l++) {   /* loop for ceil{log2(N)} */
		le = (int)pow(2,l);
		le2 = (int)(le / 2);
		uR = 1;
		uI = 0;
		sR = cos(PI / le2);
		sI = -sin(PI / le2);
		for (j=1; j<=le2; j++) {   /* loop for each sub DFT */
			//jm1 = j - 1;
			for (i=j-1; i<=N-1; i+=le) {  /* loop for each butterfly */
				ip = i + le2;
				tR = x[ip].real * uR - x[ip].imag * uI;
				tI = x[ip].real * uI + x[ip].imag * uR;
				x[ip].real = x[i].real - tR;
				x[ip].imag = x[i].imag - tI;
				x[i].real += tR;
				x[i].imag += tI;
			}  /* Next i */
			tR = uR;
			uR = tR * sR - uI * sI;
			uI = tR * sI + uI *sR;
		} /* Next j */
	} /* Next l */

	return 0;
}

/*
 * Inverse FFT Algorithm
 * === Inputs ===
 * x : complex numbers
 * N : nodes of FFT. @N should be power of 2, that is 2^(*)
 * === Output ===
 * the @x contains the result of FFT algorithm, so the original data
 * in @x is destroyed, please store them before using FFT.
 */
int ifft(TYPE_FFT *x, int N)
{
	int k = 0;

	for (k=0; k<=N-1; k++) {
		x[k].imag = -x[k].imag;
	}

	fft(x, N);    /* using FFT */

	for (k=0; k<=N-1; k++) {
		x[k].real = x[k].real / N;
		x[k].imag = -x[k].imag / N;
	}

	return 0;
}

另外，可能还需要您在其它头文件中定义COMPLEX的复数类型typedef struct {
    float real;
	float imag;
} COMPLEX;
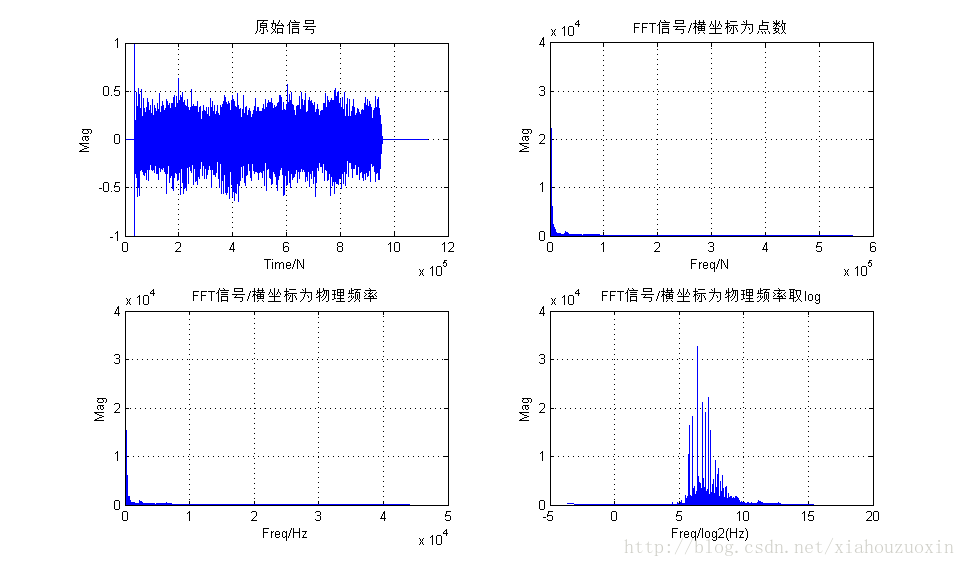
=====================增加：FFT频谱结果显示
=====================clc;
clear;

% Read a real audio signal
[fname,pname]=uigetfile(...
    {'*.wav';'*.*'},...
    'Input wav File');
[x fs nbits] = wavread(fullfile(pname,fname));

% Window
% N = 1024;
N = size(x,1);
x = x(1:N, 1);

% FFT
y = fft(x);
% 频率对称，取N/2
y = y(1:N/2);

% FFT频率与物理频率转换
x1 = 1:N/2;
x2 = (1:N/2)*fs/(N/2);  % /1000表示KHz
log_x2 = log2(x2);

% plot
figure,
subplot(2,2,1);plot(x);
xlabel('Time/N');ylabel('Mag');grid on
title('原始信号');
subplot(2,2,2);plot(x1, abs(y));
xlabel('Freq/N');ylabel('Mag');grid on
title('FFT信号/横坐标为点数');
subplot(2,2,3);plot(x2,abs(y));
xlabel('Freq/Hz');ylabel('Mag');grid on
title('FFT信号/横坐标为物理频率');
subplot(2,2,4);plot(log_x2,abs(y));
xlabel('Freq/log2(Hz)');ylabel('Mag');grid on
title('FFT信号/横坐标为物理频率取log');

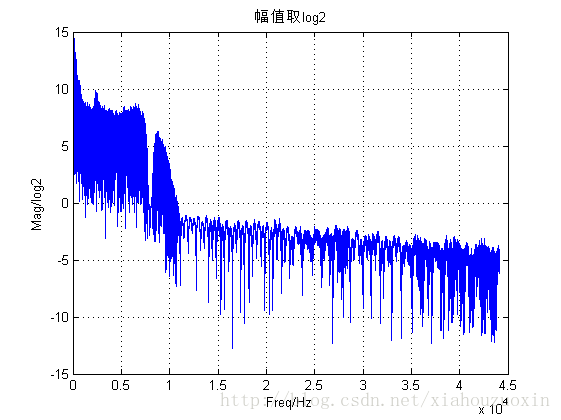
% 更常见是将幅值取log
y = log2(abs(y));
figure,
plot(x2,y);
xlabel('Freq/Hz');ylabel('Mag/log2');grid on
title('幅值取log2');




最终部分优化的源代码我放在https://github.com/xiahouzuoxin/fft。


                         
                         
     
  
      Ta的文章  更多 >> 
             
      


                    
          FFT算法的完整DSP实现
               
                0 个评论
               
              
                               

              
                  
  

  
  
    
         
  
      热门文章


      



  
    
      
      举报内容
    
    






检举类型


检举内容


检举用户




检举原因



广告推广


恶意灌水


回答内容与提问无关



抄袭答案


其他





检举说明(必填)






    

                
                 
      



    

  


 打开微信“扫一扫”，打开网页后点击屏幕右上角分享按钮
 

 





   


  
    
    



      
      
       
  
      




  
             
            
                    Copyright © 2024 平头弟 京ICP备15032243号-1
                         投诉举报邮箱：nettui@qq.com

FFT算法的完整DSP实现

1. 有关FFT理论的一点小小解释

2. FFT的DSP实现

Ta的文章 更多 >>

热门文章

举报内容

检举类型

检举原因

检举说明(必填)

打开微信“扫一扫”，打开网页后点击屏幕右上角分享按钮

Ta的文章更多 >>