{var%20f='http://v.t.sina.com.cn/share/share.php?appkey=1515056452',u=z||d.location,p=['&url=',e(u),'&title=',e(t||d.title),'&source=',e(r),'&sourceUrl=',e(l),'&content=',c||'gb2312','&pic=',e(p||'')].join('');function%20a(){if(!window.open([f,p].join(''),'mb',['toolbar=0,status=0,resizable=1,width=440,height=430,left=',(s.width-440)/2,',top=',(s.height-430)/2].join('')))u.href=[f,p].join('');};if(/Firefox/.test(navigator.userAgent))setTimeout(a,0);else%20a();})(screen,document,encodeURIComponent,'','','https://www.xiaopingtou.cn//data/attach/topic/topicKPo7gB.jpg', '推荐 guxiangguo 的文章《离散卷积运算的DSP实现》','https://www.xiaopingtou.net/article-75777.html','页面编码gb2312|utf-8默认gb2312'));){kind=link}
有关卷积的理论有很多，感觉http://www.dspguide.com/ch6/3.htm对卷积的讲解最清晰易懂，这里贴过来（如下）供参考。
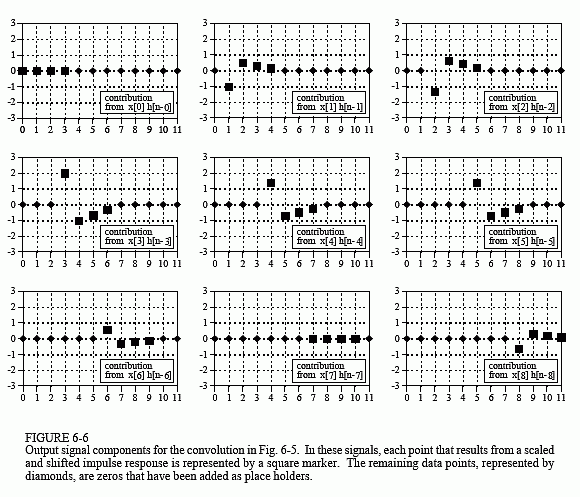
Figure 6-5 shows a simple convolution problem: a 9 point input signal,x[n], is passed through a system with a 4 point impulse response, h[n], resulting in a 9 + 4 - 1 = 12 point output signal, y[n]. In mathematical terms, x[n] is convolved with h[n] to produce y[n]. This first viewpoint of convolution is based on the fundamental concept of DSP: decompose the input, pass the components through the system, and synthesize the output. In this example, each of the nine samples in the input signal will contribute a scaled and shifted version of the impulse response to the output signal. These nine signals are shown in Fig. 6-6. Adding these nine signals produces the output signal, y[n].
Let's look at several of these nine signals in detail. We will start with sample number four in the input signal, i.e., x[4]. This sample is at index number four, and has a value of 1.4. When the signal is decomposed, this turns into an impulse represented as: 1.4δ[n-4]. After passing through the system, the resulting output component will be: 1.4h[n-4]. This signal is shown in the center box of the nine signals in Fig. 6-6. Notice that this is the impulse response, h[n], multiplied by 1.4, and shifted four samples to the right. Zeros have been added at samples 0-3 and at samples 8-11 to serve as place holders. To make this more clear, Fig. 6-6 uses squares to represent the data points that come from the shifted and scaled impulse response, and diamonds for the added zeros.
Now examine sample x[8], the last point in the input signal. This sample is at index number eight, and has a value of -0.5. As shown in the lower-right graph of Fig. 6-6, x[8] results in an impulse response that has been shifted to the right by eight points and multiplied by -0.5. Place holding zeros have been added at points 0-7. Lastly, examine the effect of points x[0] and x[7]. Both these samples have a value of zero, and therefore produce output components consisting of all zeros.
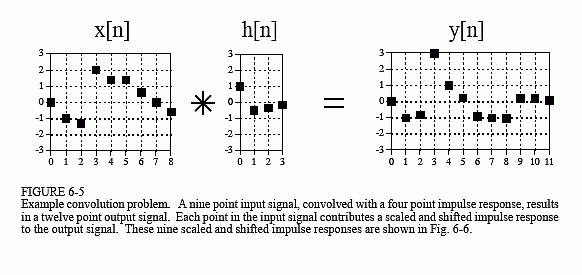
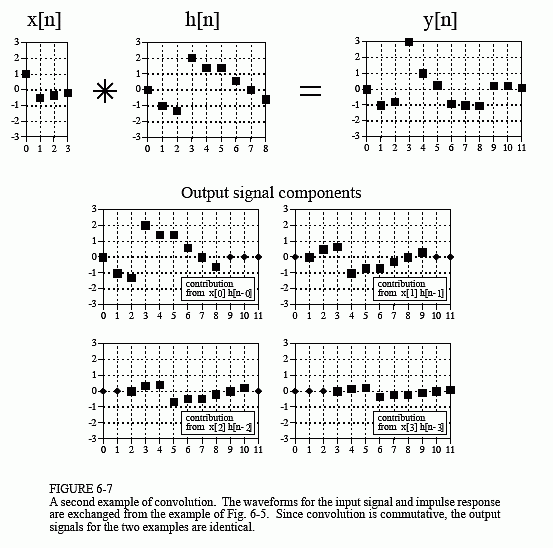
In this example, is a nine point signal and is a four point signal. In our next example, shown in Fig. 6-7, we will reverse the situation by making a four point signal, and a nine point signal. The same two waveforms are used, they are just swapped. As shown by the output signal components, the four samples in result in four shifted and scaled versions of the nine point impulse response. Just as before, leading and trailing zeros are added as place holders.
But wait just one moment! The output signal in Fig. 6-7 is identical to the output signal in Fig. 6-5. This isn't a mistake, but an important property. Convolution is commutative: a[n]*b[n] = b[n]*a[n]. The mathematics does not care which is the input signal and which is the impulse response, only that two signals are convolved with each other. Although the mathematics may allow it, exchanging the two signals has no physical meaning in system theory. The input signal and impulse response are two totally different things and exchanging them doesn't make sense. What the commutative property provides is a mathematical tool for manipulating equations to achieve various results.
A program for calculating convolutions using the input side algorithm is shown in Table 6-1. Remember, the programs in this book are meant to convey algorithms in the simplest form, even at the expense of good programming style. For instance, all of the input and output is handled in mythical subroutines (lines 160 and 280), meaning we do not define how these operations are conducted. Do not skip over these programs; they are a key part of the material and you need to understand them in detail.
The program convolves an 81 point input signal, held in array X[ ], with a 31 point impulse response, held in array H[ ], resulting in a 111 point output signal, held in array Y[ ]. These are the same lengths shown in Figs. 6-3 and 6-4. Notice that the names of these arrays use upper case letters. This is a violation of the naming conventions previously discussed, because upper case letters are reserved for frequency domain signals. Unfortunately, the simple BASIC used in this book does not allow lower case variable names. Also notice that line 240 uses a star for multiplication. Remember, a star in a program means multiplication, while a star in an equation means convolution. A star in text (such as documentation or program comments) can mean either.
The mythical subroutine in line 160 places the input signal into X[ ] and the impulse response into H[ ]. Lines 180-200 set all of the values in Y[ ] to zero. This is necessary because Y[ ] is used as an accumulator to sum the output components as they are calculated. Lines 220 to 260 are the heart of the program. The FOR statement in line 220 controls a loop that steps through each point in the input signal, X[ ]. For each sample in the input signal, an inner loop (lines 230-250) calculates a scaled and shifted version of the impulse response, and adds it to the array accumulating the output signal, Y[ ]. This nested loop structure (one loop within another loop) is a key characteristic of convolution programs; become familiar with it.
Keeping the indexing straight in line 240 can drive you crazy! Let's say we are halfway through the execution of this program, so that we have just begun action on sample X[40], i.e., I% = 40. The inner loop runs through each point in the impulse response doing three things. First, the impulse response is scaled by multiplying it by the value of the input sample. If this were the only action taken by the inner loop, line 240 could be written, Y[J%] = X[40]✳H[J%]. Second, the scaled impulse is shifted 40 samples to the right by adding this number to the index used in the output signal. This second action would change line 240 to: Y[40+J%] = X[40]*H[J%]. Third, Y[ ] must accumulate (synthesize) all the signals resulting from each sample in the input signal. Therefore, the new information must be added to the information that is already in the array. This results in the final command: Y[40+J%] = Y[40+J%] + X[40]*H[J%]. Study this carefully; it is very confusing, but very important.
理论弄明白了，本人在DSP2812上对其进行了实现，参考上面的算法伪代码很容易写出如下程序：
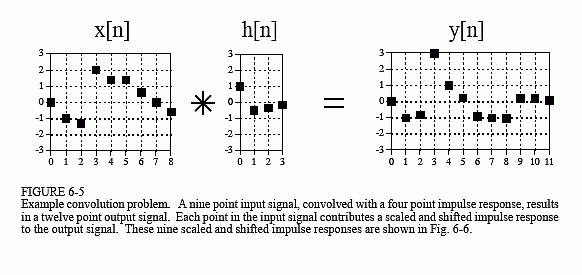
In this example, is a nine point signal and is a four point signal. In our next example, shown in Fig. 6-7, we will reverse the situation by making a four point signal, and a nine point signal. The same two waveforms are used, they are just swapped. As shown by the output signal components, the four samples in result in four shifted and scaled versions of the nine point impulse response. Just as before, leading and trailing zeros are added as place holders.
But wait just one moment! The output signal in Fig. 6-7 is identical to the output signal in Fig. 6-5. This isn't a mistake, but an important property. Convolution is commutative: a[n]*b[n] = b[n]*a[n]. The mathematics does not care which is the input signal and which is the impulse response, only that two signals are convolved with each other. Although the mathematics may allow it, exchanging the two signals has no physical meaning in system theory. The input signal and impulse response are two totally different things and exchanging them doesn't make sense. What the commutative property provides is a mathematical tool for manipulating equations to achieve various results.
A program for calculating convolutions using the input side algorithm is shown in Table 6-1. Remember, the programs in this book are meant to convey algorithms in the simplest form, even at the expense of good programming style. For instance, all of the input and output is handled in mythical subroutines (lines 160 and 280), meaning we do not define how these operations are conducted. Do not skip over these programs; they are a key part of the material and you need to understand them in detail.
The program convolves an 81 point input signal, held in array X[ ], with a 31 point impulse response, held in array H[ ], resulting in a 111 point output signal, held in array Y[ ]. These are the same lengths shown in Figs. 6-3 and 6-4. Notice that the names of these arrays use upper case letters. This is a violation of the naming conventions previously discussed, because upper case letters are reserved for frequency domain signals. Unfortunately, the simple BASIC used in this book does not allow lower case variable names. Also notice that line 240 uses a star for multiplication. Remember, a star in a program means multiplication, while a star in an equation means convolution. A star in text (such as documentation or program comments) can mean either.
The mythical subroutine in line 160 places the input signal into X[ ] and the impulse response into H[ ]. Lines 180-200 set all of the values in Y[ ] to zero. This is necessary because Y[ ] is used as an accumulator to sum the output components as they are calculated. Lines 220 to 260 are the heart of the program. The FOR statement in line 220 controls a loop that steps through each point in the input signal, X[ ]. For each sample in the input signal, an inner loop (lines 230-250) calculates a scaled and shifted version of the impulse response, and adds it to the array accumulating the output signal, Y[ ]. This nested loop structure (one loop within another loop) is a key characteristic of convolution programs; become familiar with it.
Keeping the indexing straight in line 240 can drive you crazy! Let's say we are halfway through the execution of this program, so that we have just begun action on sample X[40], i.e., I% = 40. The inner loop runs through each point in the impulse response doing three things. First, the impulse response is scaled by multiplying it by the value of the input sample. If this were the only action taken by the inner loop, line 240 could be written, Y[J%] = X[40]✳H[J%]. Second, the scaled impulse is shifted 40 samples to the right by adding this number to the index used in the output signal. This second action would change line 240 to: Y[40+J%] = X[40]*H[J%]. Third, Y[ ] must accumulate (synthesize) all the signals resulting from each sample in the input signal. Therefore, the new information must be added to the information that is already in the array. This results in the final command: Y[40+J%] = Y[40+J%] + X[40]*H[J%]. Study this carefully; it is very confusing, but very important.
理论弄明白了，本人在DSP2812上对其进行了实现，参考上面的算法伪代码很容易写出如下程序：
/*
* conv.h
* function : convolution
*
* Created on: 2013-8-3
* Author: monkeyzx
*/
#ifndef CONV_H_
#define CONV_H_
typedef short conv_type;
struct conv_signal {
conv_type *signal;
conv_type n;
};
extern struct conv_signal conv(struct conv_signal x, struct conv_signal h);
extern void zx_conv(void);
#endif /* CONV_H_ */
/*
* conv.c
*
* Created on: 2013-8-3
* Author: monkeyzx
*/
#include
#include
#include "conv.h"
conv_type x_const[9] = {0,-1,-2,2,1,1,1,0,-1};
conv_type h_const[4] = {1,-1,0,0};
static struct conv_signal x;
static struct conv_signal h;
static struct conv_signal y;
/*
* 卷积计算
* x : input signal
* h : response signal
* y : output signal
*
* Note : be careful of free y.signal in other places if y is not uesd
*/
struct conv_signal conv(struct conv_signal x, struct conv_signal h)
{
short i = 0;
short j = 0;
y.n = x.n + h.n - 1;
y.signal = (conv_type *)malloc(y.n * sizeof(conv_type));
if (!y.signal) {
y.signal = NULL;
return y;
}
/* 初始化输出y */
for (i = 0; i < y.n; i++) {
y.signal[i] = 0;
}
/* 计算卷积 */
for (i = 0; i < x.n; i++) {
for (j = 0; j < h.n; j++) {
y.signal[i+j] = y.signal[i+j] + x.signal[i]*h.signal[j];
}
}
return y;
}
/*
* routine for test
*/
void zx_conv(void)
{
int i = 0;
x.n = 9;
x.signal = (conv_type *)malloc(x.n * sizeof(conv_type));
if (!x.signal) {
return;
} else {
for (i=0; i< x.n; i++) {
x.signal[i] = x_const[i];
}
}
h.n = 4;
h.signal = (conv_type *)malloc(h.n * sizeof(conv_type));
if (!h.signal) {
free(x.signal);
return;
} else {
for (i=0; i< h.n; i++) {
h.signal[i] = h_const[i];
}
}
y = conv(x, h);
/*
* Only for debug
*/
#ifdef DEBUG
for (i=0; i
main函数中只需要调用zx_conv()函数就可以了，这里的输入信号和响应信号为
conv_type x_const[9] = {0,-1,-2,2,1,1,1,0,-1};
conv_type h_const[4] = {1,-1,0,0};
在往硬件上移植算法时有几点要注意：
（1）可以将栈设置大一些，因为这里使用到malloc函数分配存储空间
（2）移植时要将printf等函数删除，这些函数编译后代码占用存储空间太大，很可能存储器装不下，导致编译时报错
"../SRAM.cmd", line 55: error: placement fails for object ".text", size 0x1c13
(page 0). Available ranges:
PRAMH0 size: 0x1000 unused: 0xf76 max hole: 0xf76
error: errors encountered during linking; "zx_project_c2000.out" not built
这就是.text段剩余空间大小为0xf76，而带printf编译后代码大小为0x1c13，明显放不下。我们把printf去除后编译，查看Debug目录下的.map文件，其中有编译链接后段的信息，我们截取一段
SECTION ALLOCATION MAP
output attributes/
section page origin length input sections
-------- ---- ---------- ---------- ----------------
.text 0 003f8000 00000690
003f8000 000001cf rts2800_ml.lib : memory.obj (.text)
003f81cf 00000186 DSP28_DefaultIsr.obj (.text:retain)
003f8355 000000af zx_conv.obj (.text)
003f8404 0000005a rts2800_ml.lib : fs_mpy.obj (.text)
003f845e 0000004d DSP28_CpuTimers.obj (.text)
003f84ab 00000044 rts2800_ml.lib : boot.obj (.text)
003f84ef 0000002f zx_cputimer0.obj (.text)
003f851e 00000029 rts2800_ml.lib : fs_tol.obj (.text)
003f8547 00000025 zx_cputimer2.obj (.text)
003f856c 00000021 DSP28_PieCtrl.obj (.text)
003f858d 00000021 rts2800_ml.lib : memcpy_ff.obj (.text)
003f85ae 00000020 DSP28_PieVect.obj (.text)
003f85ce 0000001f DSP28_Xintf.obj (.text)
003f85ed 0000001f zx_gpio.obj (.text)
003f860c 0000001a DSP28_SysCtrl.obj (.text)
003f8626 00000019 rts2800_ml.lib : args_main.obj (.text)
003f863f 00000019 : exit.obj (.text)
003f8658 00000016 zx_func.obj (.text)
003f866e 0000000e DSP28_Gpio.obj (.text)
003f867c 00000009 rts2800_ml.lib : _lock.obj (.text)
003f8685 00000003 main.obj (.text)
003f8688 00000001 DSP28_Adc.obj (.text)
003f8689 00000001 DSP28_ECan.obj (.text)
003f868a 00000001 DSP28_Ev.obj (.text)
003f868b 00000001 DSP28_InitPeripherals.obj (.text)
003f868c 00000001 DSP28_Mcbsp.obj (.text)
003f868d 00000001 DSP28_Sci.obj (.text)
003f868e 00000001 DSP28_Spi.obj (.text)
003f868f 00000001 DSP28_XIntrupt.obj (.text)
其中zx_conv只占用了0x000000af，整个.text段占用大小为0x00000690。