class="markdown_views prism-github-gist">
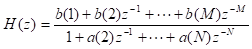
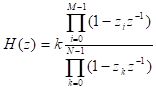 零点向量
零点向量
极点向量
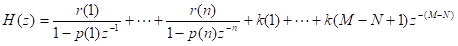 分母极点向量
分母极点向量
分子留数向量
余数多项式系数向量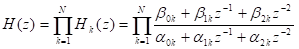 二阶因式为,
二阶因式为,
 注意,二阶因式对应的系数分别就是框图对应的系数!!!
注意,二阶因式对应的系数分别就是框图对应的系数!!!
由零极点增益转换为传递函数
由二次分式转换为零极点增益
由传递函数转换为二次分式
一、系统函数表示
1、传递函数法(tf)
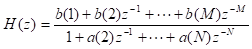
a=[1 a(2) a(3)… a(N)]
b=[b(1) b(2)… b(M)]
2、零极点增益法(zp)
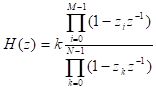 零点向量
零点向量 Z=[z1 z2 zM-1];极点向量
P=[z1,z2,…,zN-1]k为系统增益。
3、部分分式法(residue or residuez)
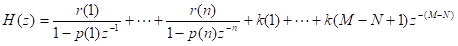 分母极点向量
分母极点向量 p=[p(1) p(2) … p(n)]分子留数向量
r=[r(1) r(2) … r(n)]余数多项式系数向量
k=[k(1) k(2) … k(M-N+1)]
4、二阶分式法(sos)
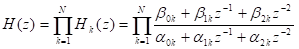 二阶因式为,
二阶因式为, 注意,二阶因式对应的系数分别就是框图对应的系数!!!
注意,二阶因式对应的系数分别就是框图对应的系数!!!(sos)
二、各表示方法的转换
1、传递函数转换为零极点增益(tf2zp)由零极点增益转换为传递函数
(zp2tf)
[z,p,k]=tf2zp(b,a)
[b,a]=zp2tf(z,p,k)
%a,b的长度要相等,不等的话要补零
2、由零极点增益转换为二次分式(zp2sos)由二次分式转换为零极点增益
(sos2zp)
[sos,g]=zp2sos(z,p,k),g为整个系统的增益,即H(z)=g*H1(z)*H2(z)…*HN(z)
sos2zp(z,p,k) =[sos,g],g为整个系统的增益,默认为1。
3、二次分式转换为传递函数(sos2tf)由传递函数转换为二次分式
(tf2sos)
[b,a]=sos2tf(sos)
[sos,g]=tf2sos(b,a)