一、什么是数字信号处理?
任何携带信息的物理量都可称为信号。我们的日产生活中到处都充满了信号,其中,有些信号是自然的,有些信号是人为的,有些信号是必需的(如语音信号),有些信号是让人愉悦的(如音乐信号),当然还有些信号是不需要的,甚至是有害的(比如工地施工产生的噪音)。因此,从一个错综复杂的信号中提取或增强有用的信号,同时抑制其中的有害或无用的信号,是数字信号处理的一种最为直接而简单的表述形式。更一般地说,信号处理是为提取、增强、存储和传输有用信息而设计的一种运算。
我们知道现实世界中的绝大多数信号都是模拟信号,比如语音、温度、电磁波、脑电图、心电图等。为了要对这些信号进行处理,我们要先将它们数字化,即必须要先将现实世界中的模拟信号转化成数字信号,然后再进行滤波、频谱分析等各种各样的数字处理。在处理完成之后,还可能要再将数字信号还原成模拟信号。比如在激光唱盘播放系统中,先要将声音信号变成数字信号存储在激光唱盘上,在回放的时候又要重新还原成模拟信号。一个典型的数字信号处理框图如下所示。ADC将模拟信号转变为数字信号,DAC将数字信号还原为模拟信号。

数字信号处理是当前科学与工程领域最为热门的技术之一,广泛应用于通信、雷达、声呐、医学成像和图像处理等许多领域,对人们的生产和生活带来了许多革命性的变化和影响。
二、从模拟信号到数字信号
在前面已经提到,自然界中的绝大多数信号都是模拟信号,为了对它们进行处理,我们首先要将模拟信号转换为数字信号。在数字信号处理中,这个过程叫做“模-数”变换(Analog-Digital,A/D)A/D变换的实现流程如下图所示,主要包括了三个步骤:采样、量化与编码。

以上三个步骤只适用于很理想的情况,但在实际应用中还有许多因素需要考虑。比如,我们在马路上采集人说话的语音信号时经常会引入周边汽车鸣笛的噪声,在采样的过程中如何才能尽量避免噪声和干扰信号的混叠呢?一个比较好的方法是在采样前添加一个预处理的过程,即抗混叠滤波器。其工作原理是利用一般不同信号的频率不同的特性(比如,人说话的频率一般是4kHZ,汽车喇叭为1kHZ左右),在频域上将噪声信号过滤掉。我们一般分析信号都是在时间域上进行分析,如何将时间域上的信号映射到频率域呢?于是这就引入了我们熟知的连续时间信号的傅里叶变换(FT)。
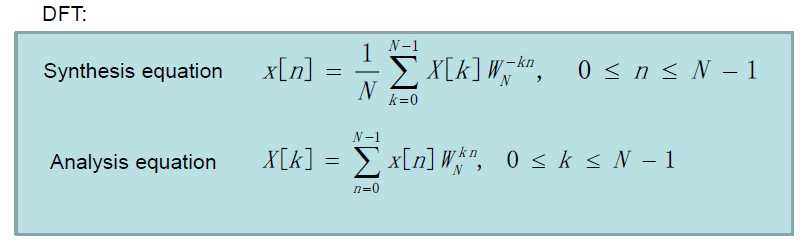
模拟信号在经过滤波后就可以对其进行接下来的采样、量化与编码操作,经过这三个步骤原先的连续时间信号变成了离散时间信号。
三、从数字信号到模拟信号
数字化后的信号经过一系列的信号处理算法之后,很多时候还需要输出模拟信号。这个过程通常称为“数-模”变换(Digital-Analog,D/A),D/A变换是A/D变换的逆过程。由采样定理可知,在满足采样定理的情况下,模拟信号和对应的数字信号完全一致。也就是说,在满足采样定理的情况下,从模拟信号能得到唯一的数字信号;反过来从数字信号也能得到唯一的模拟信号。(对采样定理不够了解的同学可参考以下连接中的博文:https://blog.csdn.net/qq_35771020/article/details/83959339)由数字信号得到模拟信号的过程有时也称为重构。从频谱的角度可以更好地理解数字信号的重构。如下图所示。
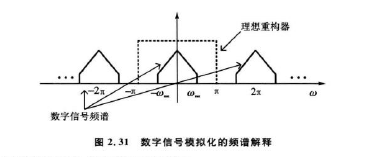
由采样定理的证明我们知道,数字信号的频谱是周期延拓的。理想情况下将数字信号通过一个理想的低通滤波器,即可得到模拟信号的频谱。为实现这个过程,我们需要将采样得到的离散时间信号从时域变换到频域进行分析,于是引入了离散时间傅里叶变换(DTFT):
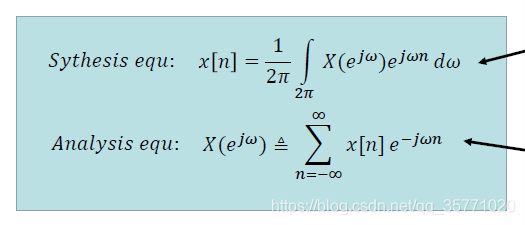
但遗憾的是经过离散时间傅里叶变换得到的信号频谱是连续的,用计算机处理还是很不方便,因此在工程上难以使用。如果能将离散信号的频谱也变成离散的,那么计算机处理起来将会高效很多。我们知道周期函数的频谱是离散的,离散函数的频谱是周期的,如果将离散函数周期化,那么我们将得到同样离散周期的频谱。基于这个原理,工程师们在实际的数字信号处理中引入了离散傅里叶变换(DFT)
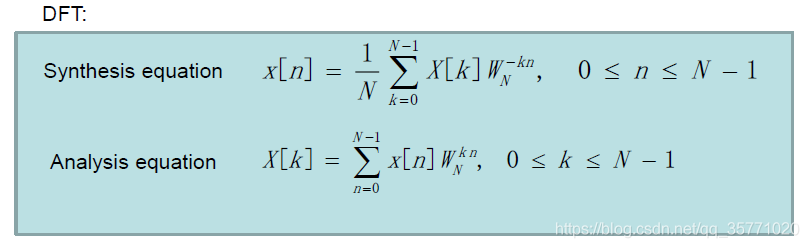
对信号进行DFT变换得到其离散周期的频谱后,我们从频谱中截取出一个周期,然后对其进行傅里叶反变换,得到原始信号发生周期延拓的周期信号,然后从这个周期信号中截取出一个周期即恢复出了原始信号。
至此,整个数字信号处理流程全部结束。
 数字信号处理是当前科学与工程领域最为热门的技术之一,广泛应用于通信、雷达、声呐、医学成像和图像处理等许多领域,对人们的生产和生活带来了许多革命性的变化和影响。
数字信号处理是当前科学与工程领域最为热门的技术之一,广泛应用于通信、雷达、声呐、医学成像和图像处理等许多领域,对人们的生产和生活带来了许多革命性的变化和影响。
 以上三个步骤只适用于很理想的情况,但在实际应用中还有许多因素需要考虑。比如,我们在马路上采集人说话的语音信号时经常会引入周边汽车鸣笛的噪声,在采样的过程中如何才能尽量避免噪声和干扰信号的混叠呢?一个比较好的方法是在采样前添加一个预处理的过程,即抗混叠滤波器。其工作原理是利用一般不同信号的频率不同的特性(比如,人说话的频率一般是4kHZ,汽车喇叭为1kHZ左右),在频域上将噪声信号过滤掉。我们一般分析信号都是在时间域上进行分析,如何将时间域上的信号映射到频率域呢?于是这就引入了我们熟知的连续时间信号的傅里叶变换(FT)。
以上三个步骤只适用于很理想的情况,但在实际应用中还有许多因素需要考虑。比如,我们在马路上采集人说话的语音信号时经常会引入周边汽车鸣笛的噪声,在采样的过程中如何才能尽量避免噪声和干扰信号的混叠呢?一个比较好的方法是在采样前添加一个预处理的过程,即抗混叠滤波器。其工作原理是利用一般不同信号的频率不同的特性(比如,人说话的频率一般是4kHZ,汽车喇叭为1kHZ左右),在频域上将噪声信号过滤掉。我们一般分析信号都是在时间域上进行分析,如何将时间域上的信号映射到频率域呢?于是这就引入了我们熟知的连续时间信号的傅里叶变换(FT)。
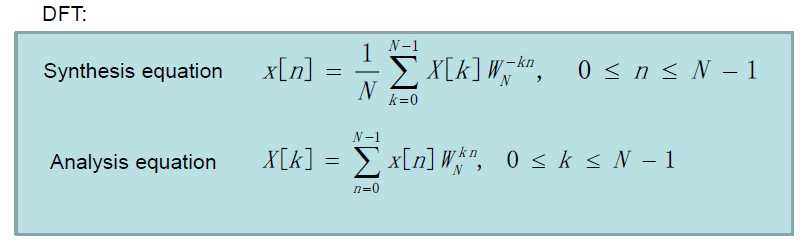 模拟信号在经过滤波后就可以对其进行接下来的采样、量化与编码操作,经过这三个步骤原先的连续时间信号变成了离散时间信号。
模拟信号在经过滤波后就可以对其进行接下来的采样、量化与编码操作,经过这三个步骤原先的连续时间信号变成了离散时间信号。
 由采样定理的证明我们知道,数字信号的频谱是周期延拓的。理想情况下将数字信号通过一个理想的低通滤波器,即可得到模拟信号的频谱。为实现这个过程,我们需要将采样得到的离散时间信号从时域变换到频域进行分析,于是引入了离散时间傅里叶变换(DTFT):
由采样定理的证明我们知道,数字信号的频谱是周期延拓的。理想情况下将数字信号通过一个理想的低通滤波器,即可得到模拟信号的频谱。为实现这个过程,我们需要将采样得到的离散时间信号从时域变换到频域进行分析,于是引入了离散时间傅里叶变换(DTFT):
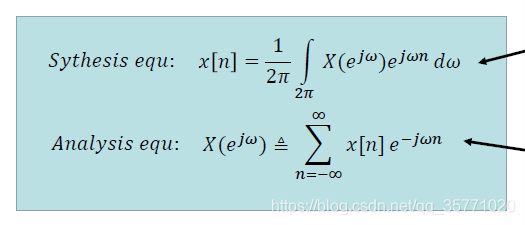 但遗憾的是经过离散时间傅里叶变换得到的信号频谱是连续的,用计算机处理还是很不方便,因此在工程上难以使用。如果能将离散信号的频谱也变成离散的,那么计算机处理起来将会高效很多。我们知道周期函数的频谱是离散的,离散函数的频谱是周期的,如果将离散函数周期化,那么我们将得到同样离散周期的频谱。基于这个原理,工程师们在实际的数字信号处理中引入了离散傅里叶变换(DFT)
但遗憾的是经过离散时间傅里叶变换得到的信号频谱是连续的,用计算机处理还是很不方便,因此在工程上难以使用。如果能将离散信号的频谱也变成离散的,那么计算机处理起来将会高效很多。我们知道周期函数的频谱是离散的,离散函数的频谱是周期的,如果将离散函数周期化,那么我们将得到同样离散周期的频谱。基于这个原理,工程师们在实际的数字信号处理中引入了离散傅里叶变换(DFT)
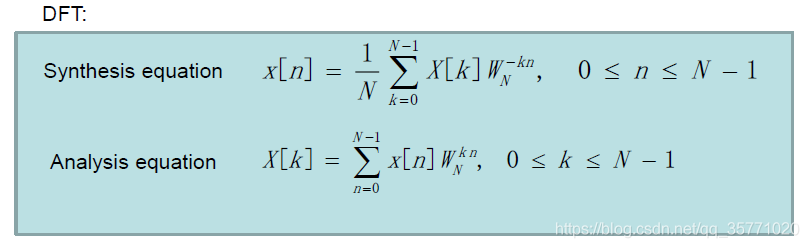 对信号进行DFT变换得到其离散周期的频谱后,我们从频谱中截取出一个周期,然后对其进行傅里叶反变换,得到原始信号发生周期延拓的周期信号,然后从这个周期信号中截取出一个周期即恢复出了原始信号。
至此,整个数字信号处理流程全部结束。
对信号进行DFT变换得到其离散周期的频谱后,我们从频谱中截取出一个周期,然后对其进行傅里叶反变换,得到原始信号发生周期延拓的周期信号,然后从这个周期信号中截取出一个周期即恢复出了原始信号。
至此,整个数字信号处理流程全部结束。