1、CVC和DSP降噪:消费者在选购蓝牙耳机时,总会听到商家在宣传耳机所具备的CVC、DSP降噪功能,不管听过N多商家这样的描述,可不少消费者依然不是很明白这两者之间的区别,针对这样的一个技术问题,我们今天来科普下这两者的工作原理及区别。 DSP是英文(digital signal processing)的简写,其工作原理:麦克风收集外部环境噪音,然后通过耳机内部的降噪系统功能,复制产生一个与外界环境噪音相等的反向声波,将噪音抵消,从而达到更好的降噪效果。
DSP是英文(digital signal processing)的简写,其工作原理:麦克风收集外部环境噪音,然后通过耳机内部的降噪系统功能,复制产生一个与外界环境噪音相等的反向声波,将噪音抵消,从而达到更好的降噪效果。 CVC是英文(Clear Voice Capture)的简写,是一种软件降噪技术,其原理是通过耳机内置的消噪软件及麦克风,来抑制多种类型的混响噪音。
CVC是英文(Clear Voice Capture)的简写,是一种软件降噪技术,其原理是通过耳机内置的消噪软件及麦克风,来抑制多种类型的混响噪音。 两者的区别:1、针对对象不一样,CVC技术主要针对通话过程中产生的回声, DSP主要是针对外部环境中的高、低频噪声。2、受益对象不同,DSP技术主要使耳机使用者本人收益,而CVC主要使通话的另一方受益。归结而言采用DSP和CVC降噪技术的耳机,都能有效降低通话外部环境的噪音,显著提高耳机的通话、听歌音质。如纳音科技最新推出的 jetblue M8 磁控蓝牙耳机,就具备DSP和CVC这两种降噪功能,在音质上表现很出 {MOD}。2、ANC降噪: ANC指Active Noise Control,主动降噪。基本原理是降噪系统产生与外界噪音相等的反向声波,将噪音中和。图1是feedforward式主动降噪耳机的示意图。ANC芯片放置在耳机内。Ref mic(reference microphone)在耳机耳罩上,采集环境噪音。Error mic(Error Microphone)在耳机内,采集降噪处理后的残差噪声。Speaker播放ANC处理后的anti-noise。
两者的区别:1、针对对象不一样,CVC技术主要针对通话过程中产生的回声, DSP主要是针对外部环境中的高、低频噪声。2、受益对象不同,DSP技术主要使耳机使用者本人收益,而CVC主要使通话的另一方受益。归结而言采用DSP和CVC降噪技术的耳机,都能有效降低通话外部环境的噪音,显著提高耳机的通话、听歌音质。如纳音科技最新推出的 jetblue M8 磁控蓝牙耳机,就具备DSP和CVC这两种降噪功能,在音质上表现很出 {MOD}。2、ANC降噪: ANC指Active Noise Control,主动降噪。基本原理是降噪系统产生与外界噪音相等的反向声波,将噪音中和。图1是feedforward式主动降噪耳机的示意图。ANC芯片放置在耳机内。Ref mic(reference microphone)在耳机耳罩上,采集环境噪音。Error mic(Error Microphone)在耳机内,采集降噪处理后的残差噪声。Speaker播放ANC处理后的anti-noise。
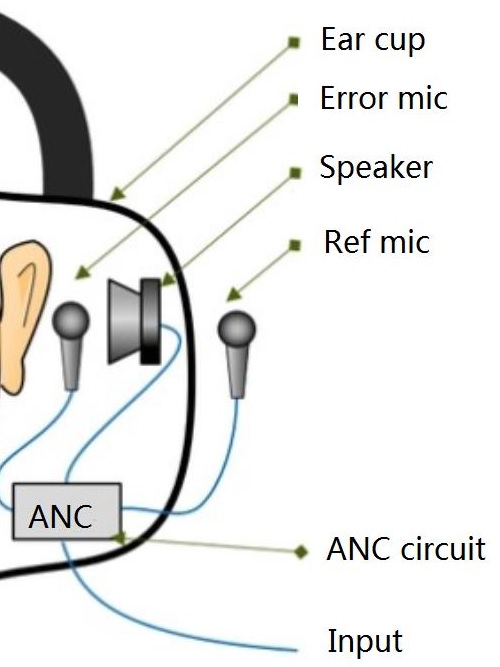
图1
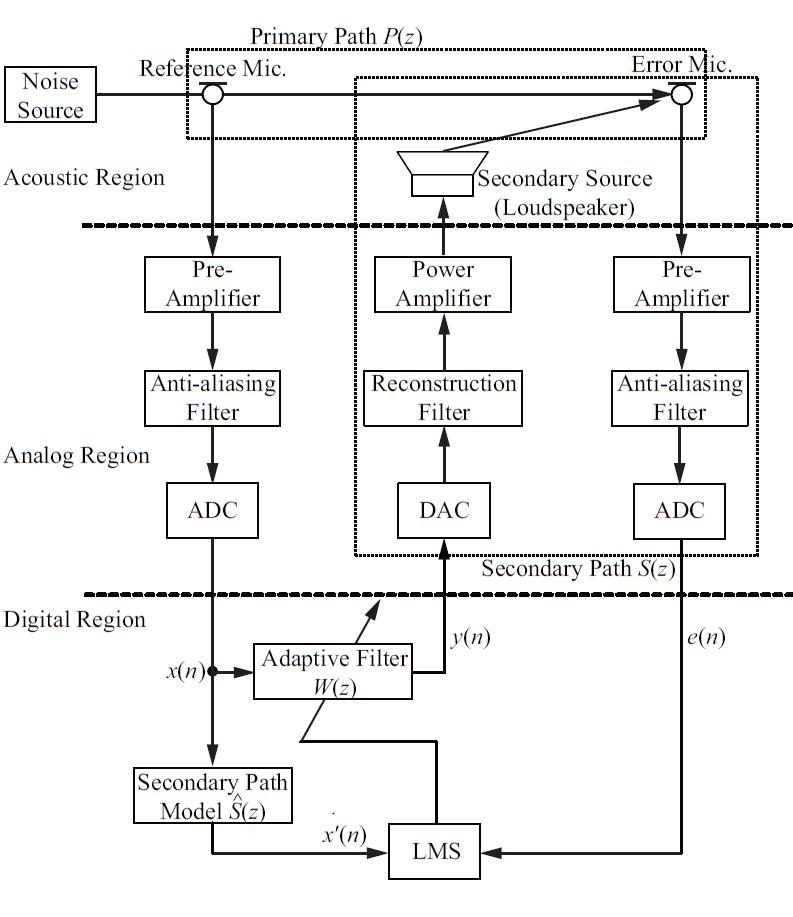
图2
图2是ANC系统的原理图,一共三层,用虚线分隔。最上一层primary path是从ref mic到error mic的声学通道,响应函数用P(z)P(z)表示;中间一层是模拟通道,其中secondary path是adaptive filter输出到返回残差的通路,包括DAC、reconstruction filter、power amplifier、speaker播放、再采集、pre-amplifier、anti-aliasing filter、ADC;最下一层是数字通路,其中adaptive filter不断调整滤波器权系数来削减残差,直到收敛。最常用的方案是用FIR滤波器结合LMS算法来实现adaptive filter。简化图2,得到图3。
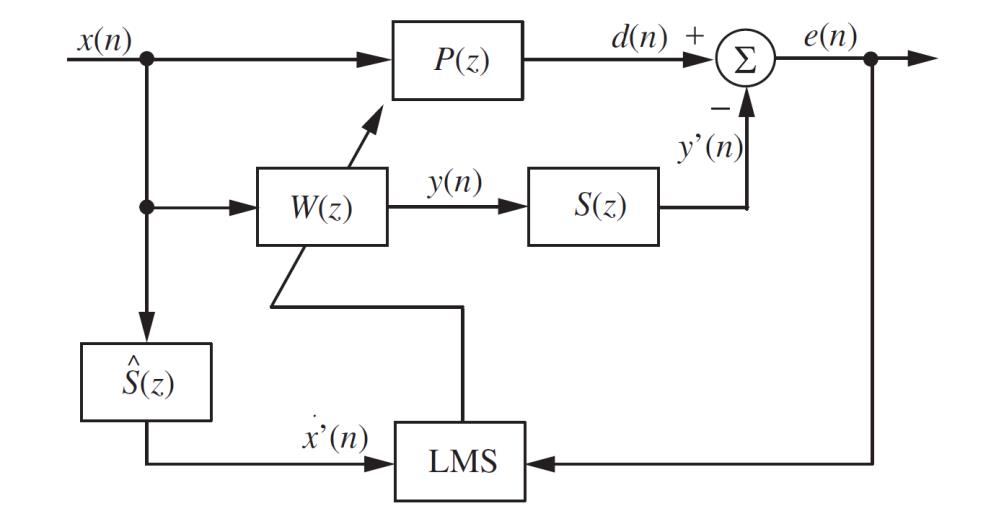
图3
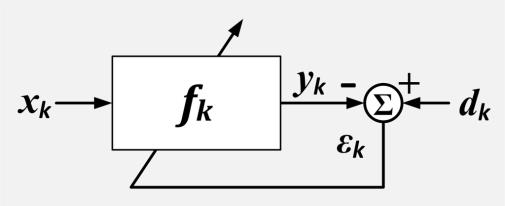
图4
所以gradient=−2e(n)s(n)∗x(n)−2e(n)s(n)∗x(n),其中s(n)s(n)未知,用其estimate近似,所以FXLMS的更新公式是w(n+1)=w(n)+μe(n)x′(n),w(n+1)=w(n)+μe(n)x′(n),其中x′(n)=sˆ(n)∗x(n)x′(n)=s^(n)∗x(n) 。 当adaptive filter收敛时,E(z)=X(z)P(z)−X(z)W(z)S(z)≈0E(z)=X(z)P(z)−X(z)W(z)S(z)≈0,因此W(z
 DSP是英文(digital signal processing)的简写,其工作原理:麦克风收集外部环境噪音,然后通过耳机内部的降噪系统功能,复制产生一个与外界环境噪音相等的反向声波,将噪音抵消,从而达到更好的降噪效果。
DSP是英文(digital signal processing)的简写,其工作原理:麦克风收集外部环境噪音,然后通过耳机内部的降噪系统功能,复制产生一个与外界环境噪音相等的反向声波,将噪音抵消,从而达到更好的降噪效果。 CVC是英文(Clear Voice Capture)的简写,是一种软件降噪技术,其原理是通过耳机内置的消噪软件及麦克风,来抑制多种类型的混响噪音。
CVC是英文(Clear Voice Capture)的简写,是一种软件降噪技术,其原理是通过耳机内置的消噪软件及麦克风,来抑制多种类型的混响噪音。 两者的区别:1、针对对象不一样,CVC技术主要针对通话过程中产生的回声, DSP主要是针对外部环境中的高、低频噪声。2、受益对象不同,DSP技术主要使耳机使用者本人收益,而CVC主要使通话的另一方受益。归结而言采用DSP和CVC降噪技术的耳机,都能有效降低通话外部环境的噪音,显著提高耳机的通话、听歌音质。如纳音科技最新推出的 jetblue M8 磁控蓝牙耳机,就具备DSP和CVC这两种降噪功能,在音质上表现很出 {MOD}。2、ANC降噪: ANC指Active Noise Control,主动降噪。基本原理是降噪系统产生与外界噪音相等的反向声波,将噪音中和。图1是feedforward式主动降噪耳机的示意图。ANC芯片放置在耳机内。Ref mic(reference microphone)在耳机耳罩上,采集环境噪音。Error mic(Error Microphone)在耳机内,采集降噪处理后的残差噪声。Speaker播放ANC处理后的anti-noise。
两者的区别:1、针对对象不一样,CVC技术主要针对通话过程中产生的回声, DSP主要是针对外部环境中的高、低频噪声。2、受益对象不同,DSP技术主要使耳机使用者本人收益,而CVC主要使通话的另一方受益。归结而言采用DSP和CVC降噪技术的耳机,都能有效降低通话外部环境的噪音,显著提高耳机的通话、听歌音质。如纳音科技最新推出的 jetblue M8 磁控蓝牙耳机,就具备DSP和CVC这两种降噪功能,在音质上表现很出 {MOD}。2、ANC降噪: ANC指Active Noise Control,主动降噪。基本原理是降噪系统产生与外界噪音相等的反向声波,将噪音中和。图1是feedforward式主动降噪耳机的示意图。ANC芯片放置在耳机内。Ref mic(reference microphone)在耳机耳罩上,采集环境噪音。Error mic(Error Microphone)在耳机内,采集降噪处理后的残差噪声。Speaker播放ANC处理后的anti-noise。 
图1
原理

图2
图2是ANC系统的原理图,一共三层,用虚线分隔。最上一层primary path是从ref mic到error mic的声学通道,响应函数用P(z)P(z)表示;中间一层是模拟通道,其中secondary path是adaptive filter输出到返回残差的通路,包括DAC、reconstruction filter、power amplifier、speaker播放、再采集、pre-amplifier、anti-aliasing filter、ADC;最下一层是数字通路,其中adaptive filter不断调整滤波器权系数来削减残差,直到收敛。最常用的方案是用FIR滤波器结合LMS算法来实现adaptive filter。简化图2,得到图3。

图3

图4
所以gradient=−2e(n)s(n)∗x(n)−2e(n)s(n)∗x(n),其中s(n)s(n)未知,用其estimate近似,所以FXLMS的更新公式是w(n+1)=w(n)+μe(n)x′(n),w(n+1)=w(n)+μe(n)x′(n),其中x′(n)=sˆ(n)∗x(n)x′(n)=s^(n)∗x(n) 。 当adaptive filter收敛时,E(z)=X(z)P(z)−X(z)W(z)S(z)≈0E(z)=X(z)P(z)−X(z)W(z)S(z)≈0,因此W(z