由于这段时间接了一个音频处理的活，不得不找一些DSP（digital signal processing）的资料，尽管上学期学过通信原理，然则实际上却不曾深入，所以现在要近乎从头做起，实在辛苦。所幸假期还长，暂且随便记录这若干天的所得。其中，大部分资料来自于《THE SCIENTIST AND ENGINEER'S GUIDE TO DIGITAL SIGNAL PROCESSING》和《DAFX》。

Linear system

线性系统要求 homogeneity（同质） 和 additivity（可叠加）.
同时，对于大多数的线性系统都有shift invariance（平移不变）
homogeneity（同质）：
如果x[n]的输入引起了y[n]的输出，那么k*x[n]将会引起k*y[n]的输出 additivity（可叠加）：
如果有输入x1[n] 引起了输出y1[n],输入x2[n] 引起输出y2[n]；那么x1[n]+x2[n]将会引起y1[n]+y2[n]。 shift invariance（平移不变）
如果x[n]的输入引起了y[n]的输出，那么x[n+s]将会引起y[n+s]的输出,其中s，是常数。

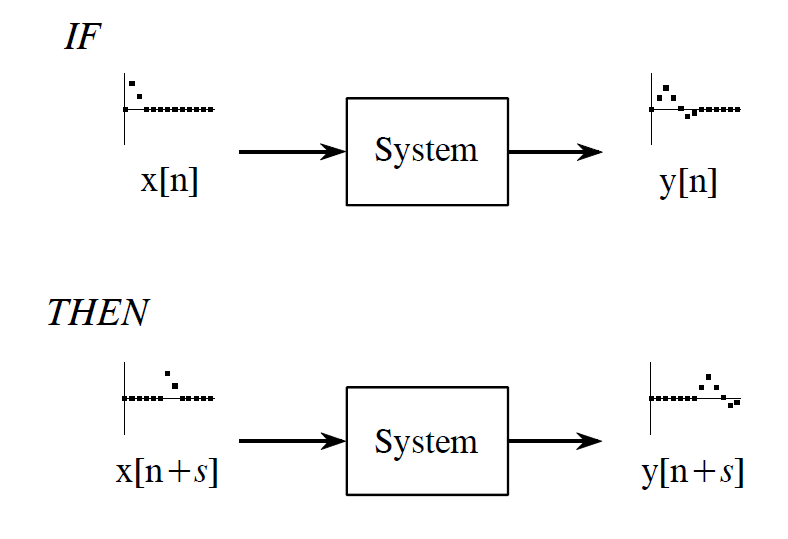
由于linear system 的这些属性，我们可以用decomposition（解构）和synthesis（重构）来处理信号。
由于对于DSP来说，信号是离散的一个个sample，所以可以针对每一个点分别作出输出，再把它们加在一起，这种方法叫做Impulse Decomposition；也可以把一个信号拆成sin和cos的叠加，这种方法叫做Fourier Decomposition（对，就是那个虐人千百遍的傅里叶）。
今天就着重谈一下Impulse Decomposition，而要谈到它，就非要牵扯Convolution（卷积）不可。 Convolution（卷积）

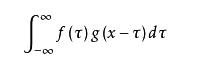
提到卷积，简直是噩梦啊，什么时域上的卷积等于频域上的乘积，什么卷积表现了时间上的叠加，诸如此类，不胜枚举。那么，卷积究竟是什么？
根据以上对线性系统的分析，可以发现，只要有两个函数，就可以完全的描述线性系统，而这两个函数就是delta function 和 impulse response；
delta function 就是狄拉克函数，也就是除了零以外的点函数值都等于零，而其在整个定义域上的积分等于1。
而impulse response（冲击响应）就是指当输入是delta function 时一个线性系统的输出函数。
由以上线性系统的三条性质可知，在已知这两者的情况下，是可以针对每一个点输入求出与之对应的输出，最后求和。这种过程，就叫做卷积，用符号表示，就是*
看图

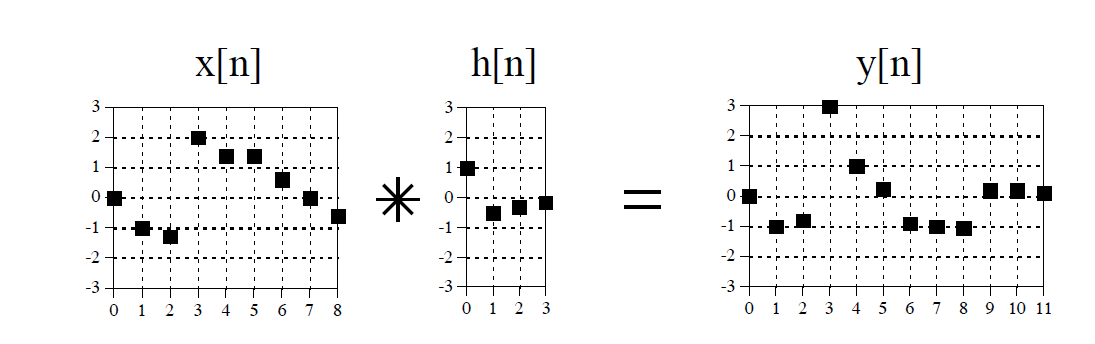
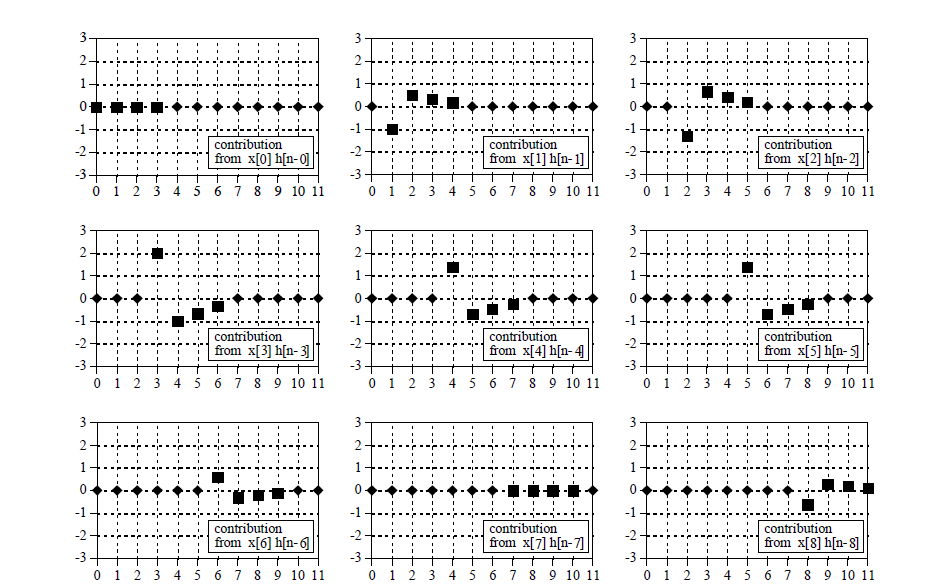
这是对离散的信号求卷积的例子。

回到标准的卷积定义，就是如上用积分定义的形式。众所周知的，积分表示求和，可以看到，它也是将一个信号先看成从原点的平移g(x-t)（shift invariance），之后乘以f(x)的值得到相应倍数的输出（homogeneity），最后求和（additivity）。
因此，离散信号的求卷积的算法也就跃然于纸上了 memset(y,0,sizeof(y)); for(int i=0;ifor(int j=0;j 其中，y代表最后求出的输出信号，x代表输入信号，h代表响应信号。INPUT_LEN代表输入信号长度，RESPONE_LEN表示响应信号长度。