本文翻译自https://www.allaboutcircuits.com/technical-articles/multiplication-examples-using-the-fixed-point-representation/
做定点数乘法的时候,首先忽略掉小数点位置,将两个乘数的补码相乘;然后再确定小数点位置。
考虑小数点位置,两个数可以表示为: a=(101001)2×(2−3)10b=(100010)2×(2−3)10a=(101001)2×(2−3)10b=(100010)2×(2−3)10
axb可以表示为 a×b=((101001)2×(2−3)10)×((100010)2×(2−3)10)a×b=((101001)2×(2−3)10)×((100010)2×(2−3)10)
即 a×b=((101001)2×(100010)2)×(2−6)10a×b=((101001)2×(100010)2)×(2−6)10 以上运算显示,在做定点小数乘法时,可以先不考虑点数的,当做整数来乘,然后将小数点放在右边起第6bit左边即可。
axb的二进制乘法过程如下:

将小数点放在结果的右边第六个bit的左边,得到结果a×b=10101.1100102=21.7812510a×b=10101.1100102=21.7812510。 例一的结果可以总结如下:
如果a、b的字长分别为Qn1.m1格式和Qn2.m2格式,那么axb格式为Qn.m。其中n=n1+n2,m=m1+m2。乘法结果字长为n+m,可以保证结果不会发生溢出。
在计算axb时,首先忽略小数点,看做整数做乘法,然后在结果的右边起第m bit的左边点小数点即可得到正确的结果。
有符号数乘以无符号数的时候,与上面不同的是,所有的部分积都是有符号的。在做有符号数加法的时候,需要对长度较短的数进行符号位扩展。因此,这里所有的部分积相加的时候需要先进行符号扩展。首先忽略小数点,我们可以得到如下计算过程:
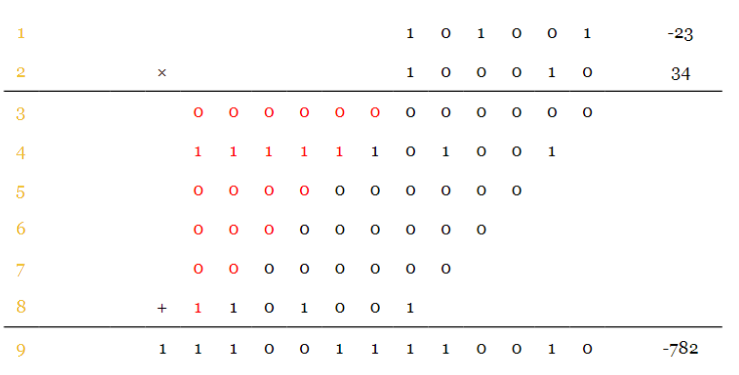
例二与例一唯一不同的地方是例二需要对部分积进行符号扩展。因为两个乘数都是6bit,相乘结果会是12bit,因此所有部分积都符号扩展到12bit。又由于所有数都是补码表示,12bit结果为模12运算,因此我们需要将结果的第13bit忽略掉。
然后考虑结果的小数点位置,可以得到
a×b=110011.1100102=−(001100.0011102)=−12.2187510a×b=110011.1100102=−(001100.0011102)=−12.2187510。该结果是和上面计算的十进制结果等效的,即−12.21875=−78264−12.21875=−78264。 例三:假设a=100.002a=100.002,b=111.1112b=111.1112,a、b均为Q3.3格式,a为有符号数,b为无符号数。求axb。
该例子的计算过程和例二相似:
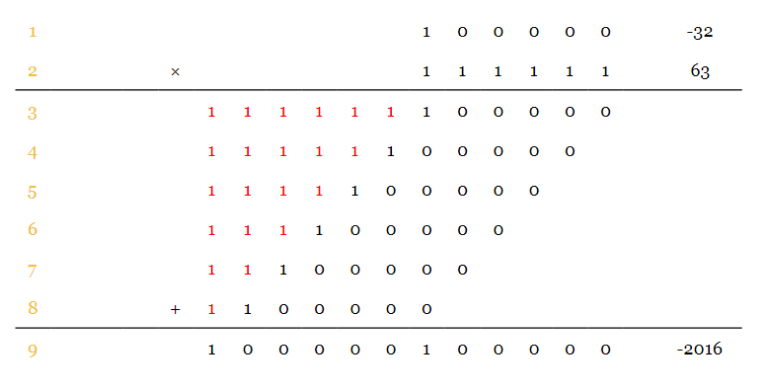
为了简化计算,可以对部分积进行两两逐步相加,每次相加后要将结果的符号位左边的值忽略掉。考虑小数点位置后得到最终结果:a×b=100000.1000002a×b=100000.1000002。 在进行接下来的讨论之前,需要回顾一下二进制补码表示的一个重要特性。
该式表示我们使用与无符号二进制数转换为十进制数相似的方法将二进制补码数转换为十进制数,不同的是这里需要将符号位乘以-1。例如假设x=1012x=1012为补码表示,则依据equation可以得到 x=−1×22+0×21+1×20=−3Equation2x=−1×22+0×21+1×20=−3Equation2
我们也可以用另一种更常用的方法得到负数补码对应的十进制数结果,即将补码再取补码然后乘以-1,即x=−(0112)=−310x=−(0112)=−310。
公式1的证明很简单。如果符号位为0,则公式1的正确性是显而易见的。假设x是一个负数,即xM−1=1xM−1=1。因为x是M bit数,其等效十进制数可以通过如下过程得到:−(two′scomplementofx)=−(2M−x)−(two′scomplementofx)=−(2M−x)。在下面的推导里,会使用脚注“Two’s Complement” 和 “Two”来区分x的二进制补码形式和x的补码的补码形式,考虑xM−1=1xM−1=1,则有: (1xM−2...x0)Two′sComplement=−(2M−(1xM−2...x0)Two)=−2M+2M−1+∑i=0M−2xi×2i=−2M−1+∑i=0M−2xi×2iEquation3(1xM−2...x0)Two′sComplement=−(2M−(1xM−2...x0)Two)=−2M+2M−1+∑i=0M−2xi×2i=−2M−1+∑i=0M−2xi×2iEquation3

该例子中最后一个部分积(第7行)需要格外注意。因为b是有符号数,b的最高位是符号位。公式3已经证明二进制补码的十进制表示可以通过将补码看做无符号数处理然后将符号位乘以-1得到。基于此特性,以上相乘运算也可以看做无符号数乘法,不同的之处是我们必须将与b的符号位相乘的系数-1考虑进来。在上面的例子中,最后一个部分积是通过计算a的补码得到的,考虑小数点位置,我们可以得到最终结果a×b=1110.0000102a×b=1110.0000102。该结果是一个有符号数。该结果表示为十进制数为a×b=−(0001.1111102)=−1.9687510a×b=−(0001.1111102)=−1.9687510,该结果与我们用十进制运算得到的结果相同:−1.96875=−12664−1.96875=−12664。
这里需要强调两点:

考虑小数点位置得到最终结果a×b=1010.1000102a×b=1010.1000102。
该例子中,最后一个部分积对被乘数取反的时候,必须先将被乘数a扩展一位得到011001011001,然后再对其进行求补码得到最后的部分积100111100111,该部分积为负数,与实际相符。如果反过来的话,我们先对a求补码得到00110011,然后在符号扩展一位得到000111000111,该计算得到正数结果,与实际不符。因此,在计算最后一个部分积的时候,对被乘数求补码必须先将其扩展一位,然后再求补码。

与有符号数乘以无符号数类似,部分积是有符号数,在做部分积相加的时候需要先进行符号位扩展。因为a、b都为5bit,因此所有部分积都符号扩展到10bit。
与无符号数乘以有符号数类似,我们必须考虑b的最高符号位,因此以上计算中最后一个部分积是通过计算a的补码得到的。在计算补码的时候,需要先将a扩展一位,然后再对其进行求补码。因为a是有符号数,对其扩展一位相当于进行符号位扩展一位。
做定点数乘法的时候,首先忽略掉小数点位置,将两个乘数的补码相乘;然后再确定小数点位置。
无符号数乘以无符号数
例一:假设a=101.0012a=101.0012,b=100.0102b=100.0102,a、b均为Q3.3格式无符号数。求axb。考虑小数点位置,两个数可以表示为: a=(101001)2×(2−3)10b=(100010)2×(2−3)10a=(101001)2×(2−3)10b=(100010)2×(2−3)10
axb可以表示为 a×b=((101001)2×(2−3)10)×((100010)2×(2−3)10)a×b=((101001)2×(2−3)10)×((100010)2×(2−3)10)
即 a×b=((101001)2×(100010)2)×(2−6)10a×b=((101001)2×(100010)2)×(2−6)10 以上运算显示,在做定点小数乘法时,可以先不考虑点数的,当做整数来乘,然后将小数点放在右边起第6bit左边即可。
axb的二进制乘法过程如下:

将小数点放在结果的右边第六个bit的左边,得到结果a×b=10101.1100102=21.7812510a×b=10101.1100102=21.7812510。 例一的结果可以总结如下:
如果a、b的字长分别为Qn1.m1格式和Qn2.m2格式,那么axb格式为Qn.m。其中n=n1+n2,m=m1+m2。乘法结果字长为n+m,可以保证结果不会发生溢出。
在计算axb时,首先忽略小数点,看做整数做乘法,然后在结果的右边起第m bit的左边点小数点即可得到正确的结果。
有符号数乘以无符号数
例二:假设a=101.0012a=101.0012,b=100.0102b=100.0102,a、b均为Q3.3格式,a为有符号数,b为无符号数。求axb。有符号数乘以无符号数的时候,与上面不同的是,所有的部分积都是有符号的。在做有符号数加法的时候,需要对长度较短的数进行符号位扩展。因此,这里所有的部分积相加的时候需要先进行符号扩展。首先忽略小数点,我们可以得到如下计算过程:

例二与例一唯一不同的地方是例二需要对部分积进行符号扩展。因为两个乘数都是6bit,相乘结果会是12bit,因此所有部分积都符号扩展到12bit。又由于所有数都是补码表示,12bit结果为模12运算,因此我们需要将结果的第13bit忽略掉。
然后考虑结果的小数点位置,可以得到
a×b=110011.1100102=−(001100.0011102)=−12.2187510a×b=110011.1100102=−(001100.0011102)=−12.2187510。该结果是和上面计算的十进制结果等效的,即−12.21875=−78264−12.21875=−78264。 例三:假设a=100.002a=100.002,b=111.1112b=111.1112,a、b均为Q3.3格式,a为有符号数,b为无符号数。求axb。
该例子的计算过程和例二相似:

为了简化计算,可以对部分积进行两两逐步相加,每次相加后要将结果的符号位左边的值忽略掉。考虑小数点位置后得到最终结果:a×b=100000.1000002a×b=100000.1000002。 在进行接下来的讨论之前,需要回顾一下二进制补码表示的一个重要特性。
二进制补码表示重要特性
假设x=(xM−1xM−2…x0)2x=(xM−1xM−2…x0)2是二进制数的补码表示,则有 x=−xM−1×2M−1+∑i=0M−2xi×2iEquation1x=−xM−1×2M−1+∑i=0M−2xi×2iEquation1该式表示我们使用与无符号二进制数转换为十进制数相似的方法将二进制补码数转换为十进制数,不同的是这里需要将符号位乘以-1。例如假设x=1012x=1012为补码表示,则依据equation可以得到 x=−1×22+0×21+1×20=−3Equation2x=−1×22+0×21+1×20=−3Equation2
我们也可以用另一种更常用的方法得到负数补码对应的十进制数结果,即将补码再取补码然后乘以-1,即x=−(0112)=−310x=−(0112)=−310。
公式1的证明很简单。如果符号位为0,则公式1的正确性是显而易见的。假设x是一个负数,即xM−1=1xM−1=1。因为x是M bit数,其等效十进制数可以通过如下过程得到:−(two′scomplementofx)=−(2M−x)−(two′scomplementofx)=−(2M−x)。在下面的推导里,会使用脚注“Two’s Complement” 和 “Two”来区分x的二进制补码形式和x的补码的补码形式,考虑xM−1=1xM−1=1,则有: (1xM−2...x0)Two′sComplement=−(2M−(1xM−2...x0)Two)=−2M+2M−1+∑i=0M−2xi×2i=−2M−1+∑i=0M−2xi×2iEquation3(1xM−2...x0)Two′sComplement=−(2M−(1xM−2...x0)Two)=−2M+2M−1+∑i=0M−2xi×2i=−2M−1+∑i=0M−2xi×2iEquation3
无符号数乘以有符号数
例四:假设a=01.0012a=01.0012,b=10.0102b=10.0102,a、b均为Q2.3格式,a为无符号数,b为有符号数。求axb。
该例子中最后一个部分积(第7行)需要格外注意。因为b是有符号数,b的最高位是符号位。公式3已经证明二进制补码的十进制表示可以通过将补码看做无符号数处理然后将符号位乘以-1得到。基于此特性,以上相乘运算也可以看做无符号数乘法,不同的之处是我们必须将与b的符号位相乘的系数-1考虑进来。在上面的例子中,最后一个部分积是通过计算a的补码得到的,考虑小数点位置,我们可以得到最终结果a×b=1110.0000102a×b=1110.0000102。该结果是一个有符号数。该结果表示为十进制数为a×b=−(0001.1111102)=−1.9687510a×b=−(0001.1111102)=−1.9687510,该结果与我们用十进制运算得到的结果相同:−1.96875=−12664−1.96875=−12664。
这里需要强调两点:
- 因为所有的除了最后一行的部分积都是无符号的,因此我们只需要对最后一个部分积进行符号扩展。
- 当计算最后一个部分积的二进制补码的时候,我们必须将被乘数扩展一位。对于上面的例子,我们先将a扩展一位得到001001001001,然后对其求补码得到部分积110111110111。这里错误的做法是先求补码1011110111,再将结果符号扩展得到110111110111。虽然在这个例子中结果没有问题,但有时候会出错。

考虑小数点位置得到最终结果a×b=1010.1000102a×b=1010.1000102。
该例子中,最后一个部分积对被乘数取反的时候,必须先将被乘数a扩展一位得到011001011001,然后再对其进行求补码得到最后的部分积100111100111,该部分积为负数,与实际相符。如果反过来的话,我们先对a求补码得到00110011,然后在符号扩展一位得到000111000111,该计算得到正数结果,与实际不符。因此,在计算最后一个部分积的时候,对被乘数求补码必须先将其扩展一位,然后再求补码。
有符号数乘以有符号数
例六:假设a=11.0012a=11.0012,b=10.0102b=10.0102,a、b均为Q2.3格式有符号数。求axb。
与有符号数乘以无符号数类似,部分积是有符号数,在做部分积相加的时候需要先进行符号位扩展。因为a、b都为5bit,因此所有部分积都符号扩展到10bit。
与无符号数乘以有符号数类似,我们必须考虑b的最高符号位,因此以上计算中最后一个部分积是通过计算a的补码得到的。在计算补码的时候,需要先将a扩展一位,然后再对其进行求补码。因为a是有符号数,对其扩展一位相当于进行符号位扩展一位。
总结
- 假设a和b分别为Qn1.m1和Qn2.m2格式,那么axb格式将会是Qn.m,其中n=n1+n1,m=m1+m2。结果长度为n+m,该长度已经足够防止所有可能的溢出。为了计算axb,我们可以先忽略a和b的小数点进行乘法操作,然后再将小数点放在从右边数第m bit的左边就可以得到正确结果。
- 我们可以使用与将无符号数转换为十进制表示相似的方法来将二进制补码转换为十进制数,不同的是需要将符号位乘以一个系数-1。
- 对于无符号数乘以符号数和符号数乘以符号数,我们必须考虑乘数的最高符号位需要乘以-1。因此最后一个部分积需要通过求被乘数的补码形式来得到。在计算补码的时候,必须先将被乘数扩展一位再求补码。
- 当部分积是有符号数的时候,在做部分积加法的时候需要先进行符号位扩展。