一、实验目的

(1)掌握用MATLAB语言进行离散时间傅里叶变换和逆变换的方法。 (2)了解用MATLAB语言进行时域抽样与信号重建的方法。 (3)进一步加深对时域信号抽样与恢复的基本原理的理解。 (4)观察信号抽样与恢复的图形，掌握采样频率的确定方法和内插公式的编程方法。

二、实验原理

1.DTFT

离散时间傅里叶变换(DTFT)是指信号在时域上为离散的，而在频域上则是连续的。 如果离散时间非周期信号为x(n)，则它的离散傅里叶变换对(DTFT)表示为 反变换为： 其中，信号的频谱为：，其中称为序列的幅度谱，称为序列的相位谱。 从离散时间傅里叶变换的定义可以看出，信号在时域上是离散的、非周期的，而在频域上则是连续的、周期性的。 实例1：求x(n)＝［0，1，2，3，4，5，6，7］，0≤n≤7的DTFT，将(－2* pi，2* pi)区间分成500份。要求：
(1)画出原信号。
(2)画出由离散时间傅里叶变换求得的幅度谱和相位谱图形。 代码： xn=0:7; n=0:length(xn)-1; w=linspace(-2*pi,2*pi,500);%将[-2*pi,2*pi]频率区间分割为500份 X=xn*exp(-1j*n'*w);%离散时间傅里叶变换，这里的1j也为i或j subplot(3,1,1),stem(n,xn);%显示原序列 ylabel('x(n)') subplot(3,1,2),plot(w,abs(X));%显示序列幅度谱 axis([-2*pi 2*pi 1.1*min(abs(X)) 1.1*max(abs(X))]) ylabel('幅度谱') subplot(3,1,3),plot(w,angle(X));%显示序列相位谱 axis([-2*pi 2*pi 1.1*min(angle(X)) 1.1*max(angle(X))]) ylabel('相位谱') 输出：
在这个例子中，最重要的就是离散时间傅里叶变换公式的理解，结合本题，可将公式写成如下矩阵形式：
那么，自然地，就可得到DTFT的matlab代码：X=xn*exp(-1j*n'*w); 注：代码中之所以将j写成1j，是因为matlab自动提示这么干，原理是可提到程序运行速度和鲁棒性。

2.信号采样

离散时间信号大多由连续时间信号(模拟信号)抽样获得。在模拟信号进行数字化处理的过程中，主要经过A/D转换、数字信号处理、D/A转换和低通滤波等过程，如下图所示。其中，A/D转换器的作用是将模拟信号进行抽样、量化、编码，变成数字信号。经过处理后的数字信号则由D/A转换器重新恢复成模拟信号。 如果A/D转换电路输出的信号频谱已经发生了混叠现象，则信号再经过后面的数字信号处理电路和D/A转换电路就没有实际使用的意义了。因此，信号进行A/D转换时，采样频率的确定是非常重要的。 表示了一个连续时间信号xa(t)、对应的抽样后获得的信号 以及对应的频谱。在信号进行处理的过程
中，要使有限带宽信号xa(t)被抽样后能够不失真地还原出原模拟信号，抽样信号p(t)的周期Ts及抽样频率Fs的取值必须符合奈奎斯特(Nyquist)定理。假定xa(t)的最高频率为fm，应有Fs≥2fm，即图中的。
因此，若Fs>=2fm时，只要将抽样信号通过一个低通滤波器，就可以不失真地还原出原信号。
（注：原信号频谱在f=fm这个点的值不为0时，要求：Fs>2fm，不能等于）

2.1对连续信号进行采样

在实际使用中，绝大多数信号都不是严格意义上的带限信号。为了研究问题的方便，我们选择两个正弦频率叠加的信号作为研究对象。 实例1：已知一个连续时间信号，f0＝1 Hz，取最高有限带宽频率fm＝5f0。分别显示原连续时间信号波形和Fs>2fm、Fs＝2fm、Fs<2fm三种情况下抽样信号的波形。
（为方便，可分别取Fs＝fm、Fs＝2fm和Fs＝3fm来研究问题。） 代码： f0=1;%信号频率 fm=5*f0;%信号在频谱的最高频率 T0=1/f0; t=-2:0.1:2; f=sin(2*pi*f0*t)+1/3*sin(6*pi*f0*t); subplot(4,1,1),plot(t,f); ylabel('f(t)') for i=1:3 fs=i*fm;%采样频率 Ts=1/fs;%采样周期，采样步长 n=-2:Ts:2;%采样 f=sin(2*pi*f0*n)+1/3*sin(6*pi*f0*n); subplot(4,1,i+1),stem(n,f); label=['fs=',num2str(i),'*fm'];%拼接字符串 ylabel(label) end 输出：
若用plot来绘制采样的图像，并让fs最大为5*fm的结果如下：

2.2.连续信号和抽样信号的频谱

根据理论分析已知，信号的频谱图可以很直观地反映出抽样信号能否恢复还原模拟信号波形。因此，我们对上述三种情况下的时域信号波形求振幅频谱，来进一步分析和证明时域抽样定理。 实例1：求解上面实例1的原连续信号波形和Fs<2fm、Fs＝2fm、Fs>2fm三种情况下的抽样信号波形所对应的幅度谱。（为方便，依旧取Fs＝fm、Fs＝2fm和Fs＝3fm来研究问题。） 代码： %第一次编写的代码 f0=1;%输入的频率 T0=1/f0; fm=5*f0;%最高频率 wm=2*pi*fm; dt=0.1; t=-2:dt:2; f=sin(2*pi*f0*t)+1/3*sin(6*pi*f0*t);%原信号 N=length(t);%时间轴上采样点数 k=0:N-1; w1=k*wm/N;%在频率轴上生成N个采样频率点 F1=f*exp(-1j*t'*w1)*dt;%对原信号进行傅里叶变换，这里的dt加不加好像无所谓 subplot(4,1,1),plot(w1,abs(F1)); axis([0 max(w1) 1.1*min(abs(F1)) 1.1*max(abs(F1))]); ylabel('f(t)振幅') for i=1:3 fs=i*fm;%采样频率 Ts=1/fs;%采样周期，采样步长 n=-2:Ts:2; f=sin(2*pi*f0*n)+1/3*sin(6*pi*f0*n);%生成抽样信号 N=length(n);%时间轴上采样点数 k=0:N-1; wm=2*pi*fs; w=k*wm/N; F=f*exp(-1j*n'*w)*Ts;%对抽样信号进行傅里叶变换，这里的TS加不加好像无所谓 subplot(4,1,i+1),plot(w,abs(F)); label=['fs=',num2str(i),'*fm']; axis([0 max(w) 1.1*min(abs(F)) 1.1*max(abs(F))]) ylabel(label) end 输出：
这样看起来，会发现fs=3*fm的图像不是f(t)原图的平移，再仔细观察之后，会发现其实是坐标的尺度不一致导致的。下面修改上面的代码，将所有图像的显示区域归一化到[0, 2* pi]。 代码： %第二次编写的代码 f0=1;%输入的频率 T0=1/f0; fm=5*f0;%最高频率 wm=2*pi*fm; dt=0.1; t=-2:dt:2; f=sin(2*pi*f0*t)+1/3*sin(6*pi*f0*t);%原信号 N=length(t);%时间轴上采样点数 k=0:N-1; w1=k*wm/N;%在频率轴上生成N个采样频率点 F1=f*exp(-1j*t'*w1)*dt;%对原信号进行傅里叶变换，这里的dt加不加好像无所谓 %-----------------与第一次编写的代码有区别的地方---start subplot(4,1,1),plot(w1/(2*pi),abs(F1));%归一化到[0,2*pi] axis([0 4*fm 1.1*min(abs(F1)) 1.1*max(abs(F1))]); %-----------------与第一次编写的代码有区别的地方---end ylabel('f(t)振幅') for i=1:3 fs=i*fm;%采样频率 Ts=1/fs;%采样周期，采样步长 n=-2:Ts:2; f=sin(2*pi*f0*n)+1/3*sin(6*pi*f0*n);%生成抽样信号 N=length(n);%时间轴上采样点数 k=0:N-1; wm=2*pi*fs; w=k*wm/N; F=f*exp(-1j*n'*w)*Ts;%对抽样信号进行傅里叶变换，这里的TS加不加好像无所谓 %-----------------与第一次编写的代码有区别的地方---start subplot(4,1,i+1),plot(w/(2*pi),abs(F));%归一化到[0,2*pi] axis([0 4*fm 1.1*min(abs(F)) 1.1*max(abs(F))]) %-----------------与第一次编写的代码有区别的地方---end label=['fs=',num2str(i),'*fm']; ylabel(label) end 输出：
由图可见，当满足Fs≥2fm条件时，抽样信号的频谱没有混叠现象；当不满足Fs≥2fm条件时，抽样信号的频谱发生了混叠，即上图第2行Fs=1*fm的频谱图，在fm＝5f0的范围内，频谱出现了镜像对称的部分。 关于连续时间信号 的傅立叶变换 ，其定义如下： 对应matlab公式：F1=f*exp(-1j*t'*w1)*dt;但是看到这里可能有点同学就有点不理解，这里的dt加不加好像都无所谓，最多只是改变了信号在纵轴的比例而已。 修改代码，得到下图，左边4个图是有加dt，右边4个图是没加dt的。
可以看到没加dt的图像的纵轴数值不一致。 对应的代码如下： %第三次编写的代码 f0=1;%输入的频率 T0=1/f0; fm=5*f0;%最高频率 wm=2*pi*fm; dt=0.1; t=-2:dt:2; f=sin(2*pi*f0*t)+1/3*sin(6*pi*f0*t);%原信号 N=length(t);%时间轴上采样点数 k=0:N-1; w1=k*wm/N;%在频率轴上生成N个采样频率点 F1=f*exp(-1j*t'*w1)*dt;%对原信号进行傅里叶变换 subplot(4,2,1),plot(w1/(2*pi),abs(F1)); axis([0 4*fm 1.1*min(abs(F1)) 1.1*max(abs(F1))]); ylabel('f(t)振幅') F2=f*exp(-1j*t'*w1); subplot(4,2,2),plot(w1/(2*pi),abs(F2)); axis([0 4*fm 1.1*min(abs(F2)) 1.1*max(abs(F2))]); for i=1:3 fs=i*fm;%采样频率 Ts=1/fs;%采样周期，采样步长 n=-2:Ts:2; f=sin(2*pi*f0*n)+1/3*sin(6*pi*f0*n);%生成抽样信号 N=length(n);%时间轴上采样点数 k=0:N-1; wm=2*pi*fs; w=k*wm/N; F=f*exp(-1j*n'*w)*Ts;%对抽样信号进行傅里叶变换 subplot(4,2,2*i+1),plot(w/(2*pi),abs(F)); label=['fs=',num2str(i),'*fm']; axis([0 4*fm 1.1*min(abs(F)) 1.1*max(abs(F))]) ylabel(label) F3=f*exp(-1j*n'*w); subplot(4,2,2*i+2),plot(w/(2*pi),abs(F3)); axis([0 4*fm 1.1*min(abs(F3)) 1.1*max(abs(F3))]) end

2.3.由内插公式重建信号

满足奈奎斯特(Nyquist)抽样定理的信号 ，只要经过一个理想的低通滤波器，将原信号有限带宽以外的频率部分滤除，就可以重建原信号，如下图（a）所示。 信号重建一般采用两种方法： 一是用时域信号与理想滤波器系统的单位冲激响应进行卷积积分来求解； 二是设计实际的模拟低通滤波器对信号进行滤波。 这里讨论第一种方法：
理想低通滤波器的频域特性为一矩形，如上图（b）所示，其单位冲激响应为 由于频域上的乘积对应时域上的卷积，则原信号为：
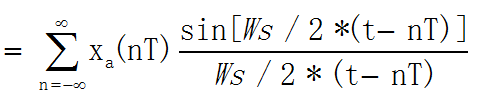其中Ws/2就为低通滤波器的截止频率。 上式称为内插公式。由式可见，xa(t)信号可以由其抽样值xa(nT)及内插函数重构。MATLAB中提供了sinc函数，可以很方便地使用内插公式。 实例：用时域卷积推导出的内插公式重建2.2实例1给定的信号。 为方便起见，截止频率就设为采样信号对应的fs，故采样公式在这里又可化简为： 代码： f0=1;%输入的频率 T0=1/f0; fm=5*f0;%最高频率 wm=2*pi*fm; dt=0.01; t=0:dt:3*T0;%选择展示3个周期的图形 x=sin(2*pi*f0*t)+1/3*sin(6*pi*f0*t);%原信号 subplot(4,1,1),plot(t,x); axis([min(t) max(t) 1.1*min(x) 1.1*max(x)]); ylabel('原信号f(t)') title('用时域信号重建抽样信号') for i=1:3 fs=i*fm;%采样频率 Ts=1/fs;%采样周期，采样步长 n=0:3*T0/Ts;%生成公式中的n序列 t1=0:Ts:3*T0;%生成公式中的t序列 x1=sin(2*pi*f0*n*Ts)+1/3*sin(6*pi*f0*n*Ts);%生成抽样信号 t_nT=ones(length(n),1)*t1-n'*Ts*ones(1,length(t1));%生成t-nT矩阵 xa=x1*sinc(pi*t_nT/Ts);%内插公式 subplot(4,1,i+1),plot(t1,xa); axis([min(t1) max(t1) 1.1*min(x1) 1.1*max(x1)]); label=['fs=',num2str(i),'*fm'];%纵轴名称 ylabel(label) end 输出： 最后的测试题目：
已知一个连续时间信号

①画出该信号及其频谱；
② 分别以抽样周期 T=1、T=pi/2 、T=2 对该信号采样，分别画出抽样信号 及其频谱；
③ 使 通过截止频率 的低通滤波器，重建信号 ，分别画出上述三个抽样周期所对应的 ，并画出 和 之间的绝对误差 ①:
代码： dt=pi/100; t=-pi:dt:pi; f=(1+cos(t))/2;%原信号 w=linspace(-2*pi,2*pi,500); F=f*exp(-1j*t'*w)*dt;%连续时间傅里叶变换 subplot(3,1,1),plot(t,f); axis([1.1*min(t) 1.1*max(t) 1.1*min(abs(f)) 1.1*max(abs(f))]) title('信号f(t)'); subplot(3,1,2),plot(w,abs(F)); axis([1.1*min(w) 1.1*max(w) 1.1*min(abs(F)) 1.1*max(abs(F))]) title('幅度谱'); subplot(3,1,3),plot(w,angle(F)); axis([1.1*min(w) 1.1*max(w) 1.1*min(angle(F)) 1.1*max(angle(F))]) title('相位谱'); 输出： ②
代码： %---------------绘制原信号-------start dt=pi/500; t=-pi:dt:pi; f=(1+cos(t))/2;%原信号 w=-2*pi:dt:2*pi;%在频率轴上生成N个采样频率点 F=f*exp(-1j*t'*w)*dt;%连续时间傅里叶变换 subplot(3,4,1),plot(t,f); axis([-2*pi 2*pi 1.1*min(f) 1.1*max(f)]) title('信号f(t)'); subplot(3,4,5),plot(w,abs(F)); axis([1.1*min(w) 1.1*max(w) 1.1*min(abs(F)) 1.1*max(abs(F))]) title('幅度谱'); subplot(3,4,9),plot(w,angle(F)); axis([1.1*min(w) 1.1*max(w) 1.1*min(angle(F)) 1.1*max(angle(F))]) title('相位谱'); %---------------绘制原信号-------end T=[1 pi/2 2];%采样周期 for i=1:3 n=-pi:T(i):pi; f=(1+cos(n))/2;%生成抽样信号 N=length(n);%时间轴上采样点数 k=0:N-1; %w1=2*pi/T(i);%角频率 %w=k*w1/N; w=-2*pi:dt:2*pi; F=f*exp(-1j*n'*w)*dt;%对抽样信号进行连续时间傅里叶变换 subplot(3,4,i+1),stem(n,f,'filled'); %axis([-pi pi 1.1*min(f) 1.1*max(f)]) new_title=['采样周期为',num2str(T(i)),'的信号']; title(new_title); subplot(3,4,i+5),plot(w,abs(F));%绘制幅度谱 %axis([1.1*min(w) 1.1*max(w) 1.1*min(abs(F)) 1.1*max(abs(F))]) title('幅度谱'); subplot(3,4,i+9),plot(w,angle(F));%绘制相位谱 %axis([1.1*min(w) 1.1*max(w) 1.1*min(angle(F)) 1.1*max(angle(F))]) title('相位谱'); end 输出：
③
代码： %---------------绘制原信号-------start dt=pi/500; t=-pi:dt:pi; f=(1+cos(t))/2;%原信号 w=-2*pi:dt:2*pi;%在频率轴上生成N个采样频率点 F=f*exp(-1j*t'*w)*dt;%连续时间傅里叶变换 subplot(3,4,1),plot(t,f); axis([-2*pi 2*pi 1.1*min(f) 1.1*max(f)]) title('信号f(t)'); subplot(3,4,5),plot(w,abs(F)); axis([1.1*min(w) 1.1*max(w) 1.1*min(abs(F)) 1.1*max(abs(F))]) title('幅度谱'); %---------------绘制原信号-------end T=[1 pi/2 2];%采样周期 T0=4.8; for i=1:3 n1=-pi:T(i):pi; f1=(1+cos(n1))/2;%生成抽样信号f(n) n=-pi/T(i):pi/T(i);%生成公式中的n序列 t1=-pi:dt:pi;%生成公式中的t序列 x1=(1+cos(n*T(i)))/2;%生成抽样信号f(nT) t_nT=ones(length(n),1)*t1-n'*T(i)*ones(1,length(t1));%生成t-nT矩阵 xa=x1*T(i)/pi*(sin(2.4*t_nT)./(t_nT));%内插公式 subplot(3,4,i+1),stem(n1,f1,'filled');%绘制原信号的采样信号fp(t) axis([-2*pi 2*pi 1.1*min(f) 1.1*max(f)]) new_title=['采样周期为',num2str(T(i)),'的信号fp(t)']; title(new_title); subplot(3,4,i+5),plot(t1,xa);%绘制采样后还原信号fr(t) axis([-2*pi 2*pi 1.1*min(xa) 1.1*max(xa)]) title('采样后还原信号fr(t)'); subplot(3,4,i+9),plot(t1,abs(xa-f));%绘制fr(t)与f(t)的绝对误差 axis([-2*pi 2*pi 1.1*min(abs(xa-f)) 1.1*max(abs(xa-f))]) title('fr(t)与f(t)的绝对误差'); end 输出：