数字信号处理最常见的面试题，请简述FIR和IIR的区别。其中的一个区别是FIR可以方便地实现线性相位。那这个线性相位指的是什么呢？先说结论，线性相位能保证信号中各频率成分的相对相位关系不改变。通俗解释是：信号经过滤波器后，各个频率分量的延时时间是一样的。本篇博客通过两个例子，延迟和全通滤波器，来解释这些概念。

1. 延迟

举一个最简单的FIR的例子，延迟。假设16kHz的采样频率，一个采样周期的延迟，可以用FIR来表示。利用Matlab来观看这个滤波器的频率响应。
注：采样频率为Fs， 采样周期为Ts，Ts = 1/Fs。 num = [0,1] den = [1,0] fvtool(num,den) 下图中，蓝 {MOD}的实线表示的幅频响应，为0dB。绿 {MOD}实现表示相频响应，主要看相频响应。图中对1k，2k，4kHz频点的横纵坐标有截图，16kHz采样率下，1kHz的正弦信号一个完整的周期（这里说的周期指的是$2pi$）内会得到16个采样值。一个采样周期的延迟，带来的相位变化是$2pi/16=pi/8=22.5degree$。而2kHz信号一个完整周期（$2pi$）内会得到8个采样值，那么一个采样周期的延迟带来的相位变化是$2pi/8=pi/4=45degree$，同理，对4kHz的信号，下图中也可以得到验证。
这个滤波器对整个信号只产生了延迟一个采样点的效果，信号的各个频率成分之间的相位关系没有改变。从这个例子可以很清楚地看到，线性相位指的是滤波器对每个频点的相频响应是一个线性关系。如下图所示，上面的图表示2kHz信号和4kHz信号，中间的图表示两者之和，下面的图表示过了一个采样周期延迟的FIR滤波器。中间的图和下面的图，这两个频率成分的信号之间相位关系没有改变。

2. 全通滤波器

全通滤波器，幅频响应为0db，但是可以改变个频率成分之间的相位关系。一阶全通滤波器有以下公式。
$A(z) =frac{c + z^{-1}}{1 + cz^{-1}}$
$c=frac{tan(pi*fc/fs) - 1}{tan(pi*fc/fs) + 1}$其中fc为截止频率，fs为采样频率。
设计一个fc = 2kHz，其幅频相频响应如下图所示。2kHz处幅频响应为$-pi/2$，4kHz处幅频响应为$-3pi/4$。很明显，这里已经不再是线性相位了。 fs = 16e3; fc = 2e3; c = (tan(pi*fc/fs) - 1)/(tan(pi*fc/fs) + 1) num = [c,1]; den = [1,c]; fvtool(num,den) 我们再将2kHz和4kHz的和通过这个全通滤波器，看看输出是怎么样的。如下图所示，经过全通滤波器后，2kHz和4kHz信号的相对相位已经改变了。2kHz延迟了$pi/2$，而4kHz延迟了$3pi/4$。最下面那幅图直接在输入信号上修改初始相位，也可以得到同样的效果。这里可以看出来，两个频率分量的相对相位关系发生了改变，两者之和的波形也发生了变化。

3.相位延迟和群延迟

以上两个例子可以看出，延迟和全通滤波器都能实现0dB的幅频响应，但相频响应区别很大。相位延迟和群延迟，就是用来描述这种不同。
对于线性时不变系统，输入为$x(t) = e^{iwt}$
输出为$y(t) = H(iw)e^{iwt} = (|H(iw)|e^{iphi(w)})e^{iwt} = |H(iw)|e^{i(phi(w)+wt)}$
其中线性系统的相频响应为
$phi(w) = arg{H(iw)}$
群延迟和相位延迟可以表示为
$au_g=-frac{dphi(w)}{dw}$
$au_phi=-frac{phi(w)}{w}$
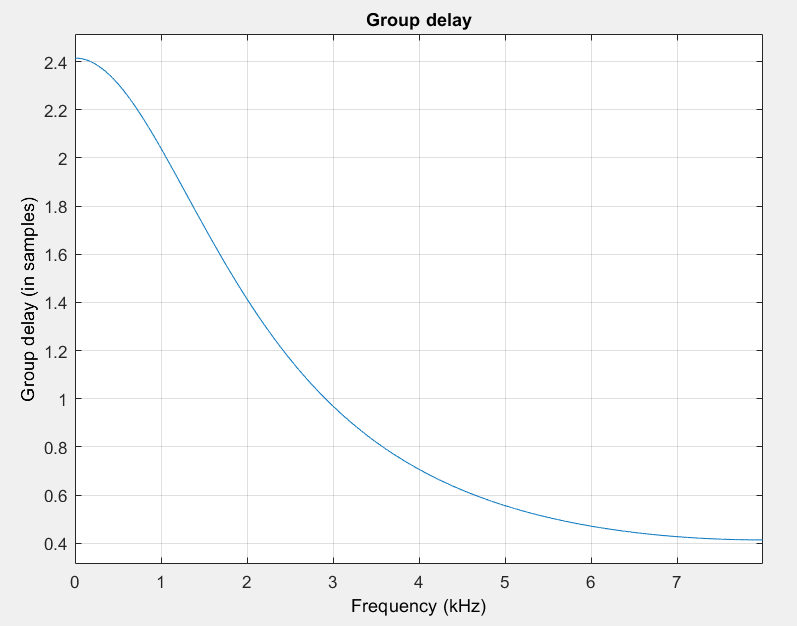
这里先解释群延迟，群延迟是相位对频率的微分。若其是非常数，信号的各频率成分的相对相位关系将发生变化，从而产生相位失真。上面两个例子的群延迟分别如下图所示，纵坐标的单位为采样周期。 延迟（FIR）的群延迟就是1个采样周期的延迟，对于每一个频率分量都是一样的。
全通滤波器（IIR）的群延迟会随频率变化，低频部分的延迟时间大于高频部分。信号经过这个系统之后，信号各频率成分的相对相位关系就改变了。

4. 实际生活中的例子

就音乐厅来说，如果把舞台上音乐家的歌唱声或乐器发出的声音作为输入，听众听到的上述声音作为输出的话，那么音乐厅可以看成输入输出之间的一个系统。最理想的情况是，输出与输入之间只有一个类似于延时的线性相位滤波器，也即是舞台上唱什么歌，听众就能听到什么歌，只是时间上稍微有滞后。 如果音乐厅这个系统不是线性相位的，会出现什么情况呢？音乐是由很多不同的频率成分构成的。这时候音乐中有些频率成分很快就从舞台上传过来了，有些频率成分则要过一阵才传过来。这样组合起来的音乐，先不论是否悦耳，至少和舞台上的已经不一样了。这时候也就意味着坐在不同位置的听众，听到的将是不同的音乐。这是人们不希望看到的。 这种情况下，必须要求线性相位的响应。（该举例转载于博客 https://blog.csdn.net/deepdsp/article/details/6804888 ）

总结：

1. 线性相位能保证信号中各频率成分的相对相位关系不改变。通俗解释是：信号经过滤波器后，各个频率分量的延时时间是一样的。
2. 延迟（FIR）和全通滤波器（IIR）都能对信号实现0dB的幅频响应。但是FIR能实现线性相位，而且群延迟为一个常数。
3. 要让信号传输不失真，这个传输系统必须具有常数幅度增益和线性相位延迟。线性时不变系统只能保证常数倍的幅度增益，并不能保证线性相位延迟。
4. 音乐厅的冲激响应必须要求线性相位。