电机控制,主要目标就是控制电机调速,调速的关键在于转矩的控制,基于坐标系的变换,最终目的是将复杂的三相交流绕组产生的磁场等效为简单的直流电机产生的磁场,电压电流同理。

ABC为三相坐标系, α β为两相正交坐标系。设三相绕组每相有效匝数为N3,两相绕组每相有效匝数为N2,各相磁动势为有效匝数与电流的乘积,其空间矢量位于相关坐标系上。
按照磁动势相等的等效原则,三相合成磁势相等,故两套绕组磁动势在α β轴上的分量都相等,因此

写成矩阵形式,得

按照变换前后总功率不变,
如果按照变换前后两套绕组产生的磁动势相同,则N3/N2=2/3。
带入图3式得
令C3/2表示从三相坐标系变换到两相正交坐标系(简称3/2变换,CLARK变换)的变换矩阵,则

利用iA+iB+iC=0的约束条件,将图4式扩展为
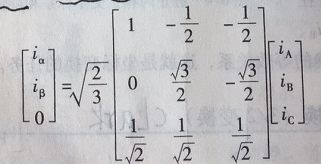
图6式第三行取作1/√2的目的是使相应的变换矩阵
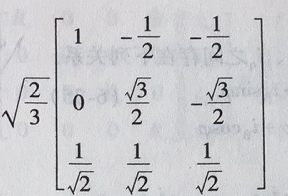
变为正交矩阵,优点在于逆矩阵等于矩阵的转置。由图6式求得逆变换
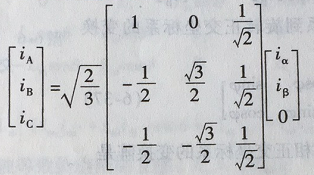
再除去第三列,即得两相正交坐标系变换到三相坐标系(简称2/3变换,CLARK逆变换)的变换矩阵
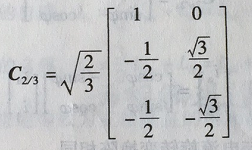
考虑到iA+iB+iC=0,带入图4式,并整理后得
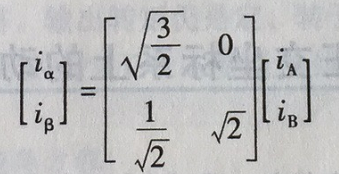
相应的逆变换
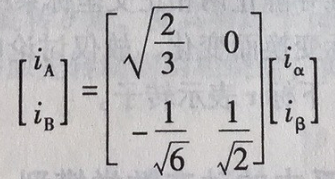
***!!!***这也是为什么在电机控制中检测电流是只需要检测两相电流的原因。
电压变换阵和磁链变换阵与电流变换阵相同。
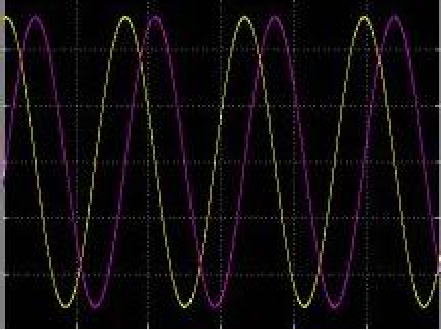
利用SIMULINK搭建的测试模型中,理想的三相定子电流如图所示,其相位互相差120度

经过CLARK变换后的等效两相交流电流如图所示,其相位相差90度。


图12中绘出了α β和dq坐标系中的磁动势矢量,绕组每相有效匝数均为N2,磁动势矢量位于相关的坐标轴上。两相交流iα、iβ和两个直流电流id、iq产生同样的以角速度ω1旋转的合成磁动势F。
由图知iα、iβ和id、iq之间存在以下关系:
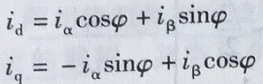
写成矩阵形式,得
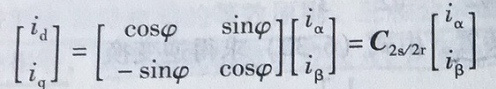
因此,静止两相正交坐标系到旋转正交坐标系的变换阵为
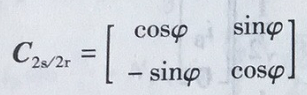
则旋转正交坐标系到静止两相正交坐标系的变换阵是
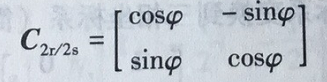
即
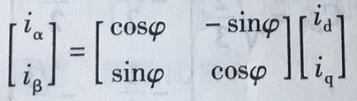
我们最终控制的电机参数依然需要交流电机的参数,所以计算等效直流电机的控制参数只是中间过程,之后再通过PARK逆变换将等效的直流电机绕组还原为等效的两相交流绕组,再将其还原为三相真实交流绕组坐标。
电压和磁链的旋转坐标变换阵与电流旋转变换相同。 利用SIMULINK搭建的测试模型中,经过CLARK变换后的等效两相交流电流如图所示,其相位相差90度

再经过PARK变换后形成的等效直流电流如图

1.CLARK(3/2)变换

ABC为三相坐标系, α β为两相正交坐标系。设三相绕组每相有效匝数为N3,两相绕组每相有效匝数为N2,各相磁动势为有效匝数与电流的乘积,其空间矢量位于相关坐标系上。
按照磁动势相等的等效原则,三相合成磁势相等,故两套绕组磁动势在α β轴上的分量都相等,因此

写成矩阵形式,得

按照变换前后总功率不变,

如果按照变换前后两套绕组产生的磁动势相同,则N3/N2=2/3。
带入图3式得

令C3/2表示从三相坐标系变换到两相正交坐标系(简称3/2变换,CLARK变换)的变换矩阵,则

利用iA+iB+iC=0的约束条件,将图4式扩展为
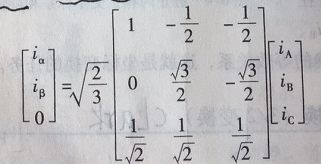
图6式第三行取作1/√2的目的是使相应的变换矩阵
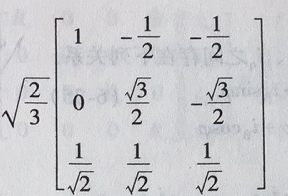
变为正交矩阵,优点在于逆矩阵等于矩阵的转置。由图6式求得逆变换
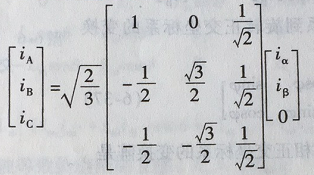
再除去第三列,即得两相正交坐标系变换到三相坐标系(简称2/3变换,CLARK逆变换)的变换矩阵
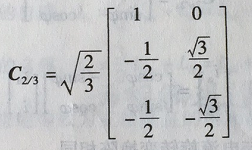
考虑到iA+iB+iC=0,带入图4式,并整理后得
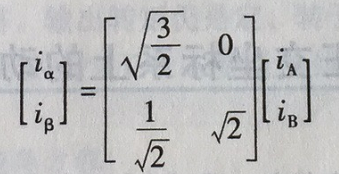
相应的逆变换
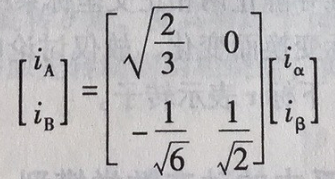
***!!!***这也是为什么在电机控制中检测电流是只需要检测两相电流的原因。
电压变换阵和磁链变换阵与电流变换阵相同。
利用SIMULINK搭建的测试模型中,理想的三相定子电流如图所示,其相位互相差120度

经过CLARK变换后的等效两相交流电流如图所示,其相位相差90度。

2.PARK(2s/2r)变换
从静止两相正交坐标系 α β到旋转正交坐标系dq的变换,称作静止两相-旋转正交变换,简称2s/2r变换,也叫PARK变换,其中s表示静止,r表示旋转,变换原则同样是产生的磁动势相等。
图12中绘出了α β和dq坐标系中的磁动势矢量,绕组每相有效匝数均为N2,磁动势矢量位于相关的坐标轴上。两相交流iα、iβ和两个直流电流id、iq产生同样的以角速度ω1旋转的合成磁动势F。
由图知iα、iβ和id、iq之间存在以下关系:
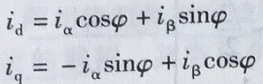
写成矩阵形式,得
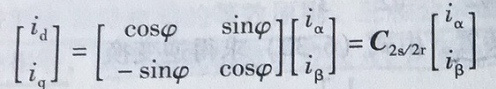
因此,静止两相正交坐标系到旋转正交坐标系的变换阵为
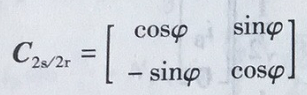
则旋转正交坐标系到静止两相正交坐标系的变换阵是
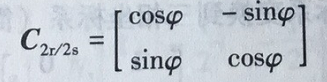
即
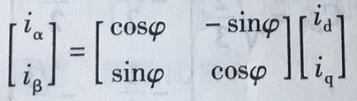
我们最终控制的电机参数依然需要交流电机的参数,所以计算等效直流电机的控制参数只是中间过程,之后再通过PARK逆变换将等效的直流电机绕组还原为等效的两相交流绕组,再将其还原为三相真实交流绕组坐标。
电压和磁链的旋转坐标变换阵与电流旋转变换相同。 利用SIMULINK搭建的测试模型中,经过CLARK变换后的等效两相交流电流如图所示,其相位相差90度

再经过PARK变换后形成的等效直流电流如图
